이제 우리는 differential module을 정의한다. 이를 위해 우리는 간단한 보조정리가 필요한데, 우선 §미분, ⁋정의 2 뒤에서 가정했던 두 번째 경우를 생각하자. 즉 우리는 commutative ring $A$, $\Delta$-graded $A$-algebra $E$, graded $A$-module $F$와 $\varepsilon$-derivation $d:E \rightarrow F$를 생각할 것이다.
미분의 functoriality
위의 가정에 더하여, 이 절에서 등장하는 모든 algebra는 unital associative이고, algebra homomorphism들도 모두 unital인 것으로 가정한다.
명제 1 두 associative unital graded $A$-algebra $E,F$가 주어졌다 하고, $M$을 $(E,E)$-bimodule, $N$을 graded $(F,F)$-bimodule이라 하자. 그럼 graded $A$-algebra homomorphism $\rho: E \rightarrow F$와, $\rho$에 의해 정의되는 $E$-bimodule들의 degree $0$ graded $E$-homomorphism $\theta: M \rightarrow N$이 주어졌다 하면 다음이 성립한다.
- 임의의 $\varepsilon$-derivation $d’: F \rightarrow N$에 대하여, $d’\circ\rho: E \rightarrow \rho^\ast N$ 또한 같은 차수의 $\varepsilon$-derivation이다.
- 임의의 $\varepsilon$-derivation $d: E \rightarrow M$에 대하여, $\theta\circ d: E \rightarrow \rho^\ast N$ 또한 같은 차수의 $\varepsilon$-derivation이다.
이에 대한 증명은 $\rho^\ast$의 정의에 의해 자명하다. 한편, 이와 같은 상황에서 우리는 $F$에도 $(E,E)$-bimodule structure를 줄 수 있다. 그렇다면 $d’:F \rightarrow N$이 언제 (left/right) $E$-linear이기도 한지를 살펴보는 것이 당연할 것이다.
명제 2 명제 1의 상황을 가정하고, $\varepsilon$-derivation $d’: F \rightarrow N$이 주어졌다 하자. 그럼 $d’$가 left (resp. right) $E$-linear한 것은 $d’$가 $F$의 subalgebra $\rho(E)$에서 항등적으로 $0$인 것과 동치이다.
이제 $\Der_A(F, N)$을 $F$에서 $N$으로 가는 $A$-derivation들의 모임으로 정의하자. 그럼 명제 2의 조건을 만족하여 $E$-linear가 되는 derivation들의 모임은 $\rho(E)$에서 identically zero인 derivation들의 모임과 같으므로 이들 모임은 $\Der_A(F, N)$의 $A$-submodule이 된다. 이를 $\Der_E(F,N)$으로 적자.
추가로 세 개의 graded $A$-algebra들 $E,F,G$가 주어졌다 하고, graded $A$-algebra homomorphism들 $\rho: A \rightarrow B$, $\sigma: B \rightarrow C$가 주어졌다 하자. 그럼 임의의 graded $A$-algebra $H$에 대하여, 다음의 세 $A$-module
\[\Der_E(F, \rho_\ast H),\qquad \Der_F(G,H),\qquad\Der_E(G, H)\]에 대하여
\[0 \rightarrow \Der_F(G, H) \rightarrow \Der_E(G,H) \rightarrow \Der_E(F, H)\]이 exact라는 것이 자명하다.
임의의 $\Delta$-graded $A$-module $M$와 $\delta\in \Delta$에 대하여, $M[\delta]$를 다음의 식
\[(M[\delta])_\mu=M_{\delta+\mu}\]으로 정의하자. 그럼 $\Delta$-graded $A$-algebra $E\oplus M[\delta]$가 존재하므로, 이제 homogeneous element $x\in E$와, 이를 사용하여 얻어지는 $E\oplus M[\delta]$의 원소 $(x,y), (x’,y’)$에 대하여 다음의 식
\[(x,y)(x',y')=(xx', xy+\varepsilon(\delta, \deg x)xy')\]을 사용하여 $E\oplus M[\delta]$ 위에 graded $A$-algebra 구조를 줄 수 있다. 이 때, projection map $\epsilon: E\oplus M[\delta] \rightarrow E$를 우리는 augmentation map이라 부르고, 이것이 graded $A$-algebra homomorphism이 된다는 것을 안다.
이제 degree $0$의 graded $A$-linear map $g:E \rightarrow E\oplus M[\delta]$이 만일 $\epsilon\circ g=\id_A$를 만족한다면, 정의에 의해 우리는 적당한 degree $\delta$ graded $A$-linear map $f:E \rightarrow M$에 대하여 $x\mapsto (x,f(x))$의 꼴이여야 한다는 것을 알고, 거꾸로 임의의 degree $\delta$ $A$-linear map $f$는 위의 조건을 만족하는 $g$를 정의한다.
그럼 다음 명제 또한 단순한 계산의 결과이다.
명제 3 Graded $K$-linear map $f: A \to E$ of degree $\delta$가 $\varepsilon$-derivation이 되기 위한 필요충분조건은, 함수 $x \mapsto (x, f(x))$가 $A$에서 $A \oplus E[\delta]$로의 graded $K$-algebra homomorphism이 되는 것이다.
한편, 역시 다음 절을 위해 앞에서 정의한 graded $A$-algebra $E\oplus M[\delta]$가 언제 associative, unital인지를 살펴볼 필요가 있다.
명제 4 위의 상황에서, $E \oplus M[\delta]$가 associative unital algebra가 되기 위한 필요충분조건은 $E$가 associative unital이며, 두 함수 $(a, x) \mapsto a \cdot x$ 및 $(a, x) \mapsto x \cdot a$가 $M$ 위에 $(A, A)$-bimodule 구조를 정의하는 것이다. 이 경우, $E \oplus M[\delta]$은 unity $(1, 0)$을 갖는다.
텐서대수와 미분
앞선 글에서 중요한 예시로 등장했던 exterior algebra는 다음과 같은 더 일반적인 세팅에서 얻어진다.
명제 5 Commutative ring $A$, $A$-module $M$에 대하여, $B=\T(M)$, $\S(M)$, $\bigwedge(M)$ 중 하나라 하고, $(B,B)$-bimodule $E$가 주어졌다 하자. 또, derivation $d_0: A \rightarrow E$와 abelian group homomorphism $d_1: M \rightarrow E$가 다음의 조건
\[d_1(ax)=ad_1(x)+d_0(a)x\]을 만족한다고 가정하자. 만일 $B=\S(M)$이라면 다음 조건
\[xd_1(y)+d_1(x)y=yd_1(x)+d_1(y)x\]을, 만일 $B=\bigwedge(M)$이라면 다음 조건
\[xd_1(x)+d_1(x)x=0\]을 추가로 가정한다. 그럼 $B$를 $\mathbb{Z}$-algebra로 보았을 때, $B$ 에서 $E$로의 유일한 $A$-derivation $d$가 존재하여 $d\vert_A = d_0$이고 $d\vert_M = d_1$을 만족하도록 할 수 있다.
증명
우선 abelian group $B \oplus E$ 위에 다음의 식
\[(b, t)(b', t') = (bb', bt' + b't)\]으로 곱셈을 정의하여 이를 associative $\mathbb{Z}$-algebra로 생각하자. 그럼 canonical injection $t\mapsto (0,t)$에 의하여 $E$를 $\mathbb{Z}$-algebra $B\oplus E$의 two-sided ideal과 동일시할 수 있으며 이 때 $E^2=0$이다.
한편, $h_0: B \to B \oplus E$를 $h_0(a) = (a, d_0(a))$로 정의하면, 이는 명제 3에 의해 (unital) ring homomorphism이며 이를 통해 $B \oplus E$는 $A$-algebra가 된다. 이제 $B\oplus E$ 위에 이러한 $A$-module 구조를 준 후 $h_1(x) = (x, d_1(x))$로 정의된 함수 $h_1: M \rightarrow B\oplus E$를 생각하자. 그럼 주어진 조건에 의하여 다음의 식
\[h_1(ax) = h_0(a) h_1(x)\]이 성립하므로, $h_1$은 $M$에서 $B$로의 $A$-linear map이다. 따라서 우리는 주어진 가정들을 사용하여, $T(M)$, $S(M)$ 혹은 $\bigwedge(M)$의 universal property를 사용하여 $h\vert_M=h_1$을 만족하는 유일한 $A$-algebra homomorphism $h:B \rightarrow B\oplus E$를 얻는다. 한편, $h$를 augmentation map $B\oplus E \rightarrow B$와 합성하면 $\id_B$가 되는 것을 쉽게 확인할 수 있으므로, 다시 명제 3에 의해 $h(b)=(b,d(b))$이도록 하는 유일한 $\varepsilon$-derivation $d:B \rightarrow E$가 존재하고 이로부터 원하는 결과를 얻는다.
Universal property
이번 절에서 임의의 algebra는 associative unital이고, algebra homomorphism도 모두 unital인 것으로 가정한다.
임의의 $A$-algebra $E$에 대하여, $E\otimes_AE$는 양 옆에 $E$의 원소를 곱해주는 방식으로 $(E,E)$-bimodule structure를 가진다. 한편 $E$의 multiplication map
\[m: E\otimes_AE \rightarrow E\]을 생각하면, $m$은 이 $(E,E)$-bimodule structure를 보존하는 것이 자명하다. 따라서 우리는 $m$의 kernel $\mathfrak{I}$를 생각할 수 있으며, 이는 $E\otimes_AE$의 sub-$(E,E)$-bimodule이다. 그럼 다음 보조정리는 단순한 계산이다.
보조정리 6 함수 $\delta_E: x \mapsto x \otimes 1 - 1 \otimes x$는 $E$에서 $\mathfrak{I}$로의 $A$-derivation이다. 뿐만 아니라, $\mathfrak{I}$는 left $A$-module로서 $\delta_E$의 image에 의해 생성된다.
증명
우선 첫째 주장은 다음의 계산
\[(xy)\otimes 1-1\otimes(xy)=(x\otimes 1-1\otimes x)y+x(y\otimes 1-1\otimes y)\]이 성립하므로 얻어진다. 이제 일반적으로 $\mathfrak{I}$의 임의의 원소 $\sum_i x_i\otimes y_i$가 주어졌다 하자. 즉 $\sum_i x_iy_i=0$이다. 이제 이로부터 다음의 식
\[\sum_i x_i\otimes y_i=\sum_i \left(x_i(1\otimes y_i)-(x_iy_i)\orimes 1\right)=\sum_i x_i(1\otimes y_i-y_i\otimes 1)\]이 얻어지므로 둘째 주장도 자명하다.
이제 이로부터 다음의 universal property를 얻는다.
명제 7 보조정리 6에서 얻어진 $\delta_E$는 다음의 universal property을 만족한다.
모든 $(E,E)$-bimodule $M$과 모든 $A$-derivation $d: E \to M$에 대하여, 유일한 $(E,E)$-bimodule homomorphism $f: \mathfrak{I} \to M$가 존재하여 $d=f\circ\delta_E$이도록 할 수 있다.
증명
우선 명제 1에 의하여 모든 $(E, E)$-bimodule homomorphism $f: \mathfrak{I} \to M$에 대해 $f \circ \delta_E$는 $E$에서 $M$으로 가는 $A$-derivation이라는 것을 안다.
한편, 유일성의 경우 $\delta_E$의 정의로부터
\[f(x \otimes 1 - 1 \otimes x) = dx\]여야 함을 알고 있고, 보조정리 6에 의하여 $\mathfrak{I}$는 $\delta_E$의 image에 의하여 유일하게 생성되므로 주어진 조건을 만족하는 $f$는 존재한다면 유일해야 한다. 추가적으로 앞선 보조정리에서의 계산을 활용하면 임의의 $\sum x_i y_i\in \mathfrak{I}$에 대하여 다음의 식
\[f\left( \sum_i x_i \otimes y_i \right) = \sum_i x_i f(1 \otimes y_i - y_i \otimes 1) = - \sum_i x_i dy_i\]이 반드시 성립해야 하는 것을 안다. 따라서 존재성을 보이기 위해서는 이것이 $(E,E)$-bimodule homomorphism인 것을 보여야 한다. 이를 위해서는 우선 mapping $(x, y) \mapsto -x \cdot dy$는 $E$에서 $M$으로 가는 $A$-bilinear mapping이므로, 이로부터 $A$-bilinear map $g: E \otimes E \to M$을 $g(x \otimes y) = -x \cdot dy$이 정의되는 것을 안다. 그럼 이를 $\mathfrak{I}$로 제한한 것이 $f$와 같고, 이제 이 $g$의 restriction이 $f$이고 이것이 $E$-bimodule 구조를 보존하는 것만 보이면 충분하고, 이는 단순한 계산이다.
위의 명제에 의하여 우리는 canonical $A$-module isomorphism
\[\Hom_{(E, E)}(\mathfrak{I}, M) \rightarrow \Der_A(E, M)\]을 얻는다. 즉 $(E,E)$-bimodule $\mathfrak{I}$는 $E$에서 $M$으로 가는 $A$-derivation들의 representation이라 생각할 수 있다.
만일 여기에 더하여, $E$가 commutative $A$-algebra라면 우리는 $E$에서 $M$으로의 derivation들의 representation를 $\lMod{E}$에서 찾을 수 있다.
우선 $E\otimes_AE$를 보자. 앞서의 논증에서 $E\otimes_AE$ 위에 정의된 $(E,E)$-bimodule structure는 다음의 식
\[x(u\otimes v)y=(xu)\otimes(vy)\]으로 주어진 것이었다. 만일 지금의 가정처럼 $E$가 commutative였다면, $E\otimes_AE$는 (commutative) ring이며 다음 식
\[x(u\otimes v)y=(xu)\otimes(vy)=(x\otimes y)(u\otimes v)\]으로부터 이 bimodule stucture가 실은 $E\otimes_AE$의 ring structure와 같은 것임을 안다. 따라서 $\mathfrak{I}$는 $E\otimes_AE$의 ideal이다.
이제 더 좋은 상황을 가정하자. 즉 $E$가 이번에는 commutative $A$-algebra라 가정하자. 그럼 임의의 $E$-module $M$은 $(E,E)$-bimodule로 볼 수 있다. 한편, 위에서 등장한 $E\otimes_AE$의 $(E,E)$-bimodule 구조는, 이번 경우에는, $E\otimes_AE$의 곱셈으로 주어지고, 따라서 $E\otimes_AE$의 sub-$(E,E)$-bimodule이었던 $\mathfrak{I}$는 이제는 $E\otimes_AE$의 ideal이 된다. 뿐만 아니라, ring에서의 multiplication map $m$은 surjective이므로 우리는 다음의 canonical isomorphism
\[(E\otimes_AE)/\mathfrak{I}\cong E\]을 얻는다.
한편, 임의의 $E$-module $M$은 그 action을 left action이자 right action으로 보는 것으로서 $(E,E)$-bimodule로 생각할 수 있다. 다른 한편으로 multiplication map $m:E\otimes_AE \rightarrow E$에 의해 $E$-module $M$를 $E\otimes_AE$-module $ M$으로 본다면, 다음의 adjoint
\[\Hom_{(E,E)}(\mathfrak{I}, M) \rightarrow \Hom_{E\otimes_AE}(\mathfrak{I}, M)\]로부터 우리는 다음 isomorphism들
\[\Hom_{E\otimes_AE}(\mathfrak{I}, M)\cong \Hom_{(E,E)}(\mathfrak{I}, M)\cong\Der_A(E, M)\]을 얻는다. 이제 우리는 여기에 더해 추가로
\[\Hom_E(\mathfrak{I}/\mathfrak{I}^2, M)\cong \Hom_{E\otimes_AE}(\mathfrak{I}, M)\cong \Hom_{(E,E)}(\mathfrak{I}, M)\cong\Der_A(E, M)\]임을 보인다. 우선 임의의 $z\in M$과 $\mathfrak{I}$의 임의의 generator $1\otimes x-x\otimes1$에 대하여, $\mathfrak{I}$를 위와 같이 $E\otimes_AE$-module로 보자. 그럼 $E$의 commutativity는 다음의 식
\[(1\otimes x-x\otimes1)z=0\]을 주므로 $\mathfrak{I}M=0$이다. 따라서 $\mathfrak{I}$는 $E\otimes_AE$-module $M$의 annihilator에 속하고, 따라서 $M$를 $(E\otimes_AE)/\mathfrak{I}$-module로 취급할 수 있다. 한편 여기에 맞추어 $A$-module $\mathfrak{I}$를 다음의 식
\[((E\otimes_AE)/\mathfrak{I})\otimes_A\mathfrak{I}\cong\mathfrak{I}/\mathfrak{I}^2\]로 바꿔주고 나면 이로부터 원하는 주장을 얻는다. 즉 다음이 성립한다.
명제 8 Commutative $A$-algebra $E$와 multiplication map $m:E\otimes_AE \rightarrow E$, 그리고 $m$의 kernel $\mathfrak{I}$를 생각하자. 그럼 canonical isomorphism
\[(E\otimes_AE)/\mathfrak{I}\cong E\]을 통해 $\mathfrak{I}/\mathfrak{I}^2$에 $E$-module structure를 주자.
한편, $\delta_{E/A}: E \rightarrow \mathfrak{I}/\mathfrak{I}^2$를 다음의 식
\[x\mapsto (x\otimes 1-1\otimes x)+\mathfrak{I}^2\]으로 정의하면, $\delta_{E/A}$는 $A$-derivation이며 다음의 universal property를 만족한다.
임의의 $E$-module $M$과 임의의 $A$-derivation $D:E \rightarrow M$이 주어질 때마다, 유일한 $A$-linear map $g:\mathfrak{I}/\mathfrak{I}^2 \rightarrow M$이 존재하여 $D=g\circ\delta_{E/A}$가 성립한다.
정의 9 $E$-module $\mathfrak{I}/\mathfrak{I}^2$는 $A$-differential들의 ($E$-)module이라 부르고 이를, $\Omega_{A}(E)$ 혹은 $\Omega_{E/A}$로 표기한다. 또, $\delta_{E/A}(x)$를 $d_{E/A}(x)$라 적으며, 혼동의 여지가 없으면 이를 간단히 $dx$라 적기도 한다. 각 $x \in E$에 대해 $d_{E/A}(x)$를 $x$의 differential이라 한다.
따라서, 우리는 다음의 canonical isomorphism
\[\Hom_E(\Omega_{E/A}, N)\cong\Der_A(E, N)\]을 얻는다.
예시 10 Commutative ring $A$와 $A$-module $M$이 주어졌다 하자. 그럼 symmetric algebra $\S(M)$은 commutative $A$-algebra이다. 따라서, 임의의 $\S(M)$-module $N$과 $A$-derivation $D:\S(M)\rightarrow N$이 주어질 때마다 다음의 식
\[D=g\circ d_{\S(M)/A}\]이 성립하도록 하는 $A$-linear map $g:\Omega_{\S(M)/A}\rightarrow N$이 유일하게 존재한다.
한편, 우리는 임의의 $A$-derivation $D:\S(M)\rightarrow L$이 주어졌을 때, 이를 $M$으로 제한한 $D\vert_M$이 $M$에서 $L$로의 $A$-module homomorphism이며, 이 대응 $D\mapsto D\vert_M$이 실은 $\S(M)$-module isomorphism이라는 것을 명제 5를 통해 확인할 쑤 있다. 한편 $L$은 $\S(M)$-module이므로 [대수적 구조] §스칼라의 변환, ⁋명제 5에 의하여
\[\Hom_{\S(M)}(M\otimes_A\S(M),L)\cong\Hom_A(M,L)\]이 성립하므로, 이를 종합하면 임의의 $A$-derivation $D:\S(M)\rightarrow N$은 canonical homomorphism
\[M\rightarrow M\otimes_A\S(M);\qquad x\mapsto x\otimes1\]를 확장하여 얻어지는 $A$-derivation $D_0$과, 적당한 $h\in \Hom_{\S(M)}(M\otimes_A\S(M),L)$에 대하여 $D=h\circ D_0$의 꼴로 적을 수 있다는 것을 안다.
간단한 계산으로 첫째 계산에서 $N=M\otimes_A\S(M)$일 때 얻어지는 $A$-linear map $\Omega_{\S(M)/A}\rightarrow M\otimes_A\S(M)$과, 둘째 계산에서 $L=\Omega_A(\S(M))$일 때 얻어지는 $h$는 서로의 역함수이며 따라서 isomorphism
\[\Omega_{\S(M)/A}\cong M\otimes_A\S(M)\]이 성립함을 알고, 뿐만 아니라 이 isomorphism을 $\omega:M\otimes_A\S(M)\rightarrow\Omega_{\S(M)/A}$이라 적는다면 임의의 $x\in M$에 대하여 $\omega(x\otimes1)=d_{\S(M)/A}(x)=dx$임을 안다.
특히, 만일 $M$이 free $A$-module of finite rank $n$이라면, $\S(M)$은 polynomial algebra $A[\x_1,\ldots, \x_n]$과 identify할 수 있으며 이 identification 하에서 $d\x_i$들은
이제 $\Omega_{E/A}$의 성질들을 보이자. 앞으로 모든 ring은 commutative이고, 모든 algebra도 associative, commutative, unital algebra이며 algebra homomorphism도 unital이다.
명제 11 다음의 commutative diagram
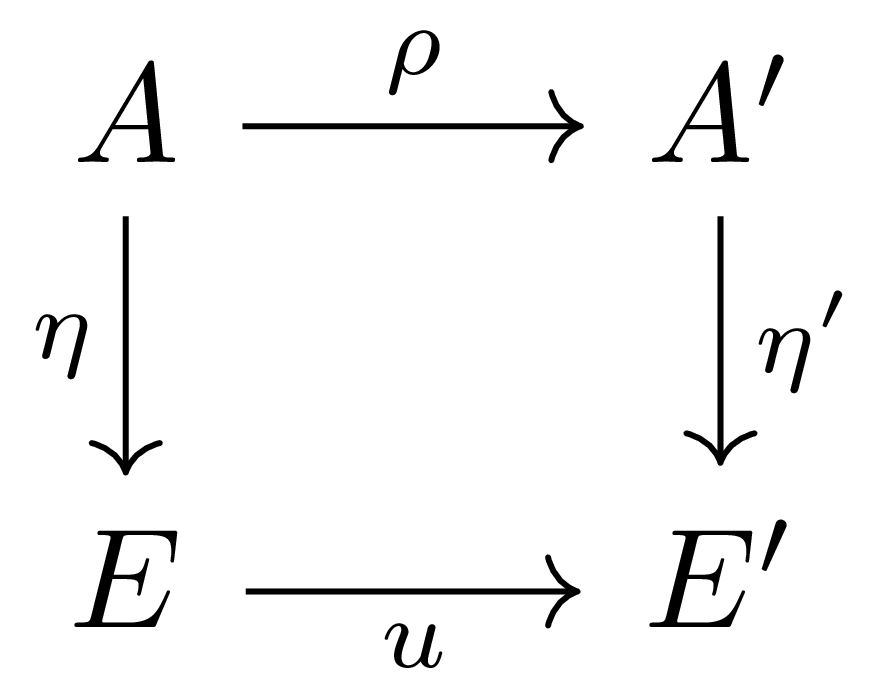
이 주어졌다 하고, 수직방향의 함수들을 통해 $E,E’$를 각각 $A,A’$-algebra로 생각하자. 그럼 다음의 diagram
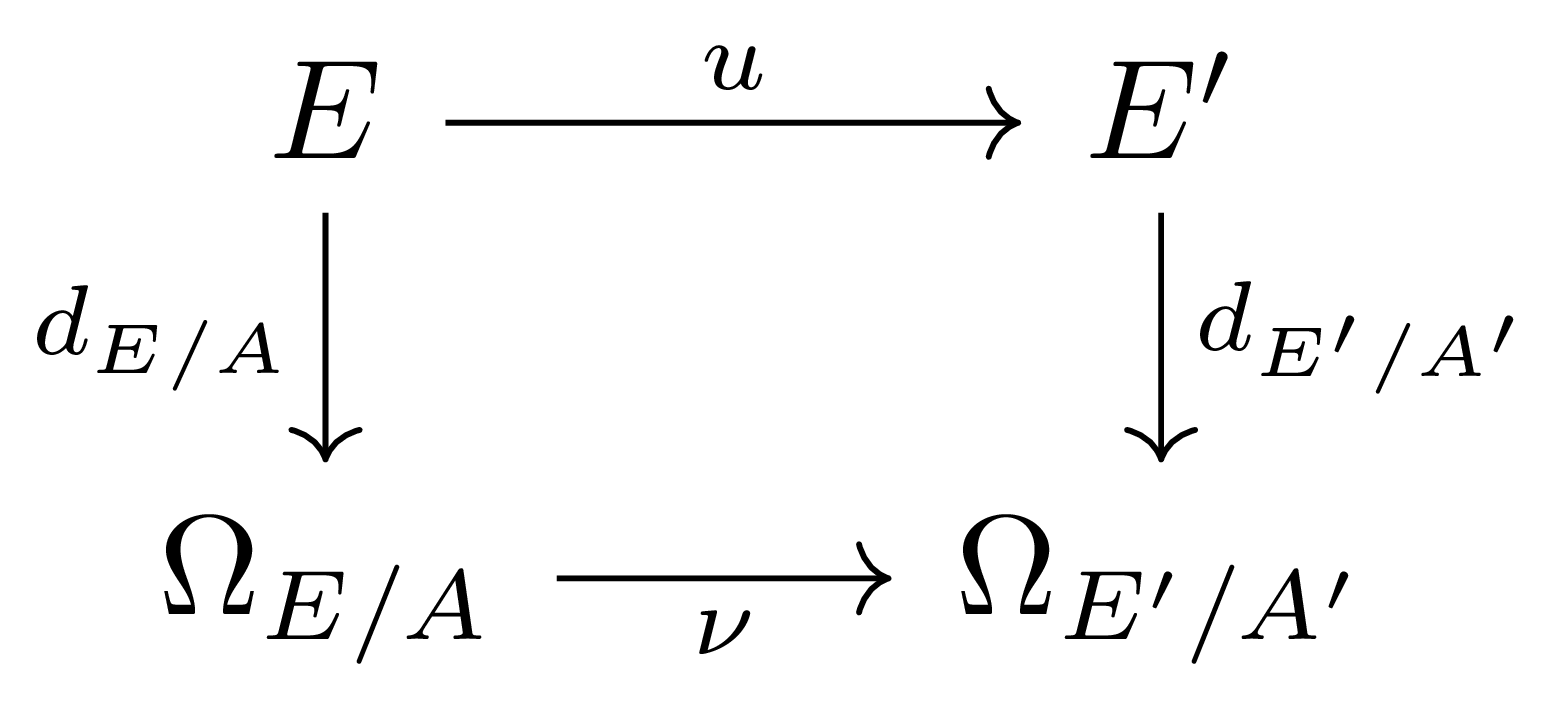
을 commute하게 하는 유일한 $A$-linear mapping
\[\nu: \Omega_{E/A} \rightarrow \Omega_{E'/A'}\]가 존재한다.
증명
이에 대한 증명은 명제 8을 증명할 때 쓰였던 다른 universal property들을 적절히 이용한 것에 불과하다.
이로부터 $\Omega$를 $A$-algebra $A \rightarrow E$를 받아 그 differential들의 module $\Omega_A(E)$를 내놓는 대응으로 본다면, $\Omega$는 functoriality 또한 갖는다는 것을 안다.
한편 $\Omega_{A’}(E’)$는 $A’$-module이므로, [대수적 구조] §스칼라의 변환, ⁋명제 5에 의하여 우리는 명제 11로부터 다음의 $A’$-linear map
\[\Omega_0(u):\Omega_A(E)\otimes_E E'\rightarrow\Omega_{A'}(E')\]를 얻으며, $i_E$를 canonical morphism $\Omega_A(E)\rightarrow \Omega_A(E)\otimes_EE’$라 하면 $\Omega(u)=\Omega_0(u)\circ i_E$임을 안다.
한편 명제 8의 universal property가 주는 다음의 isomorphism
\[\Hom_E(\Omega_A(E), M)\cong\Der_A(E, M)\]을 생각하면, 우리는 다음의 commutative diagram
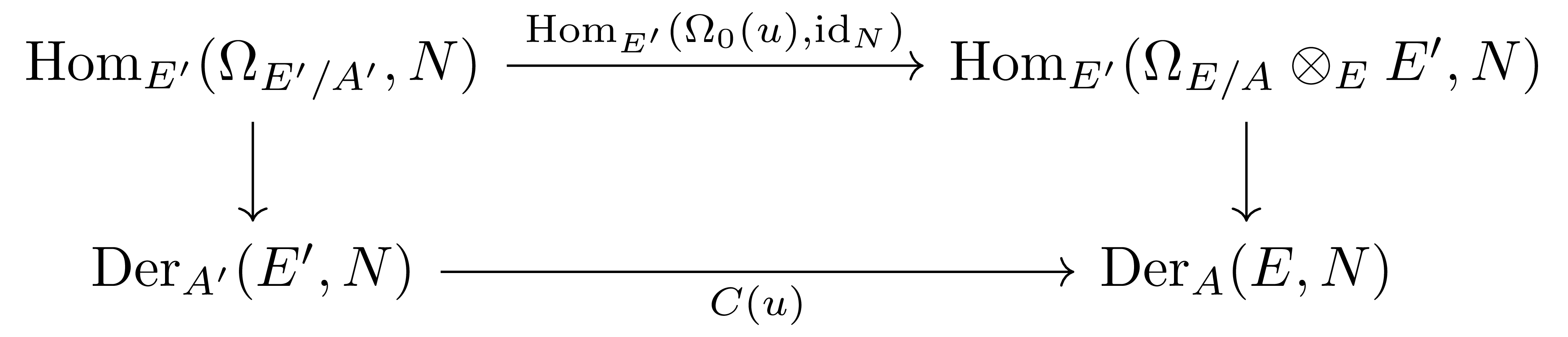
을 얻는다. 여기서 오른쪽의 수직방향 함수는 위의 isomorphism과 [대수적 구조] §스칼라의 변환, ⁋명제 5의 isomorphism을 합친
\[\Hom_{E'}(\Omega_A(E)\otimes_EE', N) \rightarrow \Hom_E(\Omega_A(E), N)\rightarrow\Der_A(E, N)\]이고 아래쪽 수평방향의 함수는 $\Der$의 functoriality로부터 얻어지는
\[\Der_{A'}(E', N) \rightarrow \Der_A(E, N);\qquad D\mapsto D\circ u\]이다.
명제 12 $E’ = E \otimes_AA’$라고 하고, $\eta : A \to E’$, $u : E \to E’$를 canonica morphism들이라 하면, $A’$-linear map
\[\Omega_0(u) : \Omega_{E/A}\otimes_EE'\rightarrow\Omega_{E'/A'}\]는 isomorphism이다.
증명
우선 수직방향 함수들이 모두 isomorphism이므로, $C(u)$가 isomorphism인 것을 보이면 임의의 $N$에 대해
\[\Hom_{E'}(\Omega_{E'/A'} , N) \rightarrow \Hom_{E'}(\Omega_{E/A}\otimes_AE',N)\]이 isomorphism이라는 것을 안다. 즉, 다음의 sequence
\[0\rightarrow\Hom_{E'}(\Omega_{E'/A'} , N) \rightarrow \Hom_{E'}(\Omega_{E/A}\otimes_AE',N)\rightarrow 0\]가 임의의 $N$에 대하여 exact이다. 이제 $\Hom$이 left exact functor이므로 (§사영가군, 단사가군, 평탄가군, ⁋명제 2) 위의 sequence가 모든 $N$에 대해 exact라는 것은 다음의 sequence
\[0 \rightarrow\Omega_{E/A}\otimes_EE'\rightarrow\Omega_{E'/A'}\rightarrow 0\]이 exact라는 것과 동치이다. 따라서 주장을 보이기 위해서는 $C(u)$가 bijective라는 것만 보이면 충분하다.
우선
\[\Hom(u, \id_N):\Hom_{A'}(E\otimes_AA', N) \rightarrow \Hom_A(E, N)\]는 isomorphism이고, $C(u)$는 이를 $\Der_{A’}(E’, N)$으로 제한한 것에 불과하므로 $C(u)$가 injective임은 자명하다. $C(u)$가 surjective라는 것 또한 어렵지 않게 증명할 수 있다.
특별히 $\rho:A \rightarrow A’$가 $\id_A: A\rightarrow A’$이고, 따라서 $u:E\rightarrow E’$가 $A$-algebra homomorphism인 경우를 생각하자. 그럼 위의 과정을 통해 $u$는 $E’$-linear homomorphism
\[\Omega_0(u): \Omega_{E/A}\otimes_AE'\rightarrow\Omega_{E'/A}\]을 유도한다. 한편, $E’$를 $E\rightarrow E’$를 사용하여 $E$-algebra로 취급하면, 여기에서 얻어지는 derivation $d_{E’/E}: E’ \rightarrow\Omega_{E’/E}$는 $A$-derivation이기도 하므로 $\Omega_{E’/A}$의 universal property에 의하여 다음의 factorization
\[E'\overset{d_{E'/A}}{\longrightarrow}\Omega_{E'/A}\overset{\Omega_u}{\longrightarrow}\Omega_{E'/E}\]이 존재한다. 그럼 다시 universal property에 의하여 다음의 commutative diagram

이 존재한다.
이제 자주 쓰이는 두 개의 exact sequence를 소개한다.
명제 13 $E’$-module들의 sequence
\[\Omega_A(E)\otimes_EE'\overset{\Omega_0(u)}{\longrightarrow}\Omega_{E'/A}\overset{\Omega_u}{\longrightarrow}\Omega_{E'/E}\longrightarrow0\]가 exact이다.
증명
다시 $\Hom$이 left exact functor라는 사실로부터 (§사영가군, 단사가군, 평탄가군, ⁋명제 2) 다음의 sequence
\[0 \rightarrow \Hom_{E'}(\Omega_{E'/E},N) \rightarrow \Hom_{E'}(\Omega_{E'/A}, N) \rightarrow \Hom_{E'}(\Omega_{E/A}\otimes_EE',N)\]가 임의의 $E’$-module $N$에 대하여 exact라는 것을 보이면 충분하다. 그런데 명제 12 이전과 이후에 사용한 commutative diagram을 이용하면, 이를 derivation들의 module들의 sequence
\[0 \rightarrow \Der_E(E', N) \rightarrow \Der_A(E', N) \rightarrow \Der_A(E, N)\]으로 바꿀 수 있으며, 이것이 exact라는 것은 명제 2 직후에 보였다.
이번에는 특히 $u:E \rightarrow E’$가 surjective이고, 따라서 $\mathfrak{I}=\ker u$에 대하여 isomorphism $E’\cong E/\mathfrak{I}$인 경우를 생각하자. 그럼 canonical derivation $d=d_{E/A}$의 $\mathfrak{I}$로의 restriction
\[\mathfrak{I}\overset{d\vert_{\mathfrak{I}}}{\longrightarrow}\Omega_{E/A}\overset{i_E}{\longrightarrow}\Omega_{E/A}\otimes_EE'\]을 $d’$라 하면, 임의의 $x,y\in \mathfrak{I}$에 대하여
\[d'(xy)=d(xy)\otimes1=dy\otimes u(x)+dx\otimes u(y)=0\]이므로 다음의 $E$-linear map
\[\overline{d}:\mathfrak{I}/\mathfrak{I}^2\rightarrow\Omega_{E/A}\otimes_EE'\]이 잘 정의된다. 뿐만 아니라 $\mathfrak{I}$가 $\mathfrak{I}/\mathfrak{I}^2$를 annihilate하므로, $\overline{d}$는 $E’=E/\mathfrak{I}$-linear map이다.
명제 14 위의 상황에서, 다음의 $E’=\mathfrak{I}/\mathfrak{I}^2$-linear map들의 sequence
\[\mathfrak{I}/\mathfrak{I}^2\overset{\overline{d}}{\longrightarrow}\Omega_{E/A}\otimes_EE'\overset{\Omega_0(u)}{\longrightarrow}\Omega_{E'/A}\longrightarrow0\]이 exact이다.
증명
앞선 논증의 표기에서, 우리는 $\Omega_{E/A}\otimes_EE’$를 $\Omega_{E/A}/\mathfrak{I}\Omega_{E/A}$와 identify할 수 있다. 그럼 이 identification 하에서, $\overline{d)$의 image는 $d(\mathfrak{I})\subset\Omega_{E/A}$의 quotient module $\Omega_{E/A}/\mathfrak{I}\Omega_{E/A}$에서의 image가 된다. 따라서, $\Omega_{E/A}$의 $A$-submodule $I$를 $\mathfrak{I}\Omega_{E/A}$와 $d(\mathfrak{I})$에 의해 생성되는 것으로 잡으면 다음의 isomorphism
\[\frac{\Omega_{E/A}\otimes_EE'}{\im(\overline{d})}\cong\frac{\Omega_{E/A}}{I}\]을 얻으며, 이를 통해 원하는 결과를 얻는다.

댓글남기기