대수적 확장

체의 확장

우리는 §체, ⁋명제 2에 의하여 field들 사이의 morphism은 injective이거나 zero map 뿐이라는 것을 살펴보았다. 이번 글에서 우리는 전자의 경우에 대하여 살펴본다.

우리는 field morphism 중 injective인 것을 field extension이라 부른다. 그럼 고정된 field \(\mathbb{K}\in\Field\)에 대하여, \(\mathbb{K}\)의 under category는 \(\mathbb{K}\)의 extension들의 category가 된다.

[범주론] §범주, ⁋예시 13의 표기법과는 다소 차이가 있으나, 우리는 field extension \(\mathbb{K}\rightarrow \mathbb{L}\)을 종종 \(\mathbb{L}/\mathbb{K}\)와 같이 표기한다. 그럼 field extension \(\mathbb{L}/\mathbb{K}\)가 주어질 때마다 우리는 injective map \(\mathbb{K}\hookrightarrow\mathbb{L}\)을 통해 \(\mathbb{K}\)를 \(\mathbb{L}\)의 subfield와 identify할 수 있다. 그러나, 만일 \(\mathbb{L}=\mathbb{K}\)이고 \(\mathbb{K}\hookrightarrow\mathbb{L}=\mathbb{K}\)이 endomorphism인 경우, 이러한 identification은 혼동의 여지가 있으므로 이 경우에는 \(\mathbb{K}\)와 \(\mathbb{L}\)의 subfield를 identify하지 않는다.

정의에 의하여, 두 extension \(\mathbb{K} \rightarrow \mathbb{L}_1\)과 \(\mathbb{K} \rightarrow \mathbb{L}_2\)가 주어졌다 하면, 다음 commutative diagram

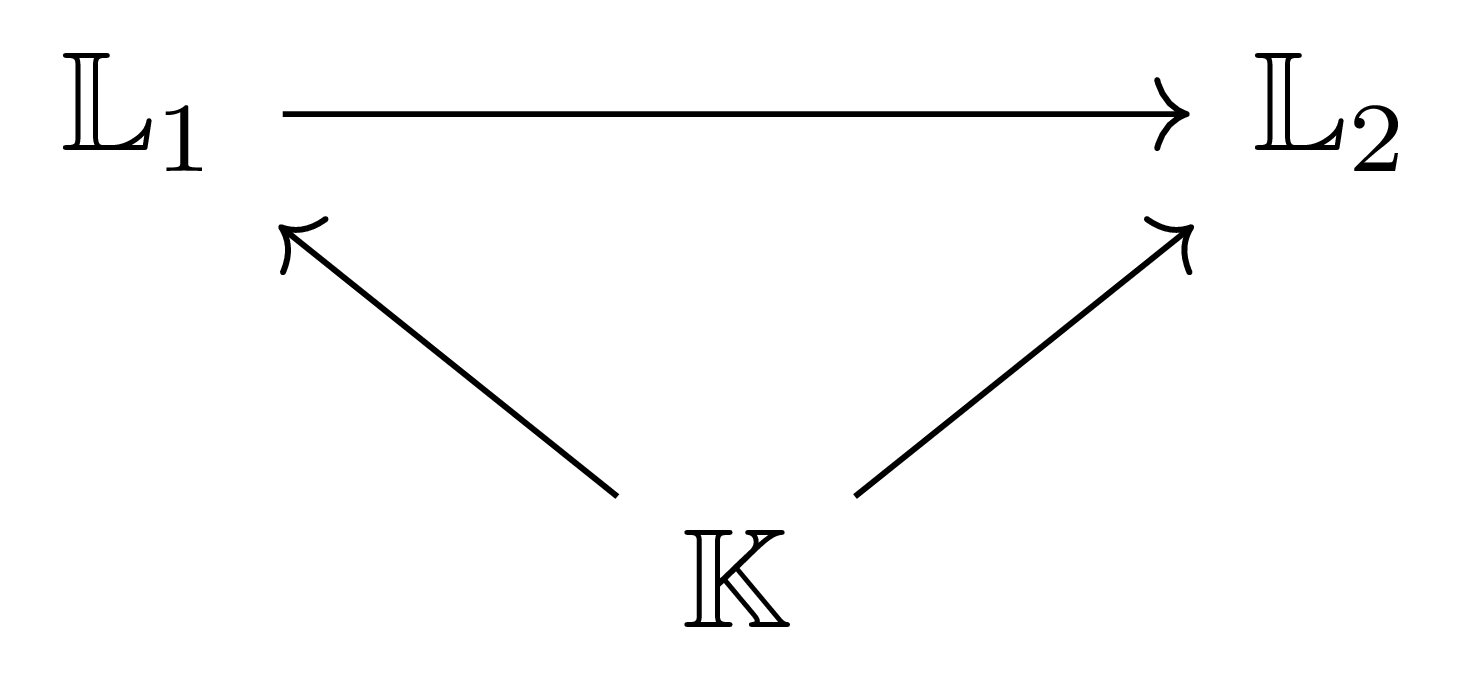
이 이들 사이의 morphism이 된다. 이 때, \(\mathbb{L}_1\)과 \(\mathbb{L}_2\)는 모두 field이므로, morphism \(\mathbb{L}_1 \rightarrow \mathbb{L}_2\)는 반드시 injective여야 한다. 위의 주의사항을 지키는 선에서, 이 경우 우리는 \(\mathbb{L}_1\)이 \(\mathbb{L}_2\)의 subextension이라 부른다.

따라서 임의의 field extension \(\mathbb{L}/\mathbb{K}\)는 (그 자체가 field인) associative unital \(\mathbb{K}\)-algebra로 생각할 수 있다.

참고 우리가 \(\mathbb{K}\)-algebra와 이들 사이의 homomorpihsm을 생각하는 것은 위와 유사한 경우를 다루기 위해서이므로, 앞으로의 글에서 category \(\Alg{\mathbb{K}}\)는 항상 unital associative \(\mathbb{K}\)-algebra들의 category가 될 것이다. 즉, 앞으로 \(\mathbb{K}\)-algebra라고 함은 항상 unital associative \(\mathbb{K}\)-algebra가 될 것이며, \(\mathbb{K}\)-algebra homomorphism 또한 unital \(\mathbb{K}\)-algebra homomorpihsm을 의미할 것이다.

임의의 \(\mathbb{K}\)-algebra는 \(\mathbb{K}\)-module이기도 하므로 그 차원이 잘 정의된다. ([다중선형대수학] §기저, ⁋명제 6)

정의 1 임의의 \(\mathbb{K}\)-algebra \(A\)에 대하여, \(\dim_{\mathbb{K}}A\)을 \(A\)의 degree라 부르고 \([A:\mathbb{K}]\)로 표기한다.

그럼 다음은 정의로부터 자명하다.

명제 2 Field extension \(\mathbb{L}_2/\mathbb{L}_1/\mathbb{K}\)에 대하여, \([\mathbb{L}_2:\mathbb{K}]=[\mathbb{L}_2:\mathbb{L}_1][\mathbb{L}_1:\mathbb{K}]\)이 성립한다.

더 일반적으로 field \(\mathbb{K}\)와 임의의 \(\mathbb{K}\)-algebra \(E\)에 대하여, \([E:\mathbb{K}]\)를 \(\dim_\mathbb{K}E\)로 정의할 수 있다. 그럼 다음 명제는 간단한 선형대수학이다.

명제 3 Finite degree \(\mathbb{K}\)-algebra \(E\)에 대하여, 만일 \(x\in E\)가 \(E\)의 non-zerodivisor라면, \(x\)는 \(E\)의 invertible element이다.

증명

가정에 의해 $$E$$는 유한차원 $$\mathbb{K}$$-algebra이며, $$x$$가 $$E$$의 non-zerodivisior이므로 다음의 함수 $$E \rightarrow E;\qquad y\mapsto xy$$ 는 injective이다. 이제 $$E$$는 유한차원이므로 위의 linear map이 injective인 것은 surjective인 것과 동치이고, 따라서 $$xy=1$$이도록 하는 $$y\in E$$가 존재하고 이로부터 원하는 결과를 얻는다.

특히 만일 유한차원 \(\mathbb{K}\)-algebra \(E\)가 integral domain이라면, \(E\)는 반드시 field이다.

한편 우리는 임의의 ring \(A\)에 대하여, \(A\)를 계수로 갖는 변수 \(\x\)에 대한 polynomial ring을 \(A[\x]\)로 표기했으며, 이는 \(A\)와 변수 \(\x\)를 포함하는 가장 작은 algebra라고 생각할 수 있다. 비슷한 방식으로 field \(\mathbb{K}\)에 원소 \(\x\)를 추가하기 위해서는, 이번에는 역수들 또한 추가해주어야 할 것이다.

정의 4 Field extension \(\mathbb{L}/\mathbb{K}\)와 부분집합 \(A\subseteq \mathbb{L}\)에 대하여, \(A\)를 포함하는 \(\mathbb{L}\)의 subextension 중 가장 작은 것을 \(\mathbb{K}(A)\)로 표시한다.

이 정의에서 \(\mathbb{L}\)은 오직 \(A\)를 정의하기 위해서만 필요하며, 실제로 \(\mathbb{L}\)이 무엇인지와는 상관 없이 \(\mathbb{K}(A)\)는 isomorphic한 field가 될 것이다. 이러한 이유로 우리는 종종 \(\mathbb{K}\)의 (아주 큰) field extension \(\Omega\)를 하나 잡아두고 (\(\Omega\)가 무엇인지는 신경쓰지 않고) 이 extension의 부분집합 \(M,N\)을 생각하기도 한다.

명제 5 \(\mathbb{K}\)의 적당한 extension의 두 부분집합 \(M,N\)에 대하여 다음의 식

\[K(M \cup N) = K(M)(N) = K(N)(M)\]

이 성립한다.

이에 대한 증명은 정의의 최소성에 의해 거의 자명하다.

한편 정의 4의 field \(\mathbb{K}(A)\)를 얻기 위해서는 \(\mathbb{K}\)의 extension \(\mathbb{L}\)을 하나 고정한 다음, \(A\)를 포함하는 \(\mathbb{L}\)의 모든 subextension들을 교집합하면 될 것이다. 한편, 우리는 \(\mathbb{K}\)의 extension들의 category에서의 morphism은 오직 extension 뿐임을 보였으므로, 다음이 성립한다.

명제 6 \(\mathcal{F}\)를 field \(E\)의 subfield들의 집합이라고 하고, 여기에 포함관계 \(\subseteq\)를 사용하면 directed set이 된다. 특히, \(\mathcal{F}\)에 속한 field들의 합집합 \(L\)은 field이다.

만일 \(\mathbb{L}=\mathbb{K}(A)\)이도록 하는 유한집합 \(A\)가 존재한다면, extension \(\mathbb{L}/\mathbb{K}\)를 finite extension이라 부른다. 그럼 특히 finite degree field extension은 finite extension이다. \(\mathbb{L}\)을 \(\mathbb{K}\)-벡터공간으로서의 basis가 \(\mathbb{L}\)의 field로서의 generator가 될 것이기 때문이다.

이제 두 개의 \(\mathbb{K}\)-extension \(\mathbb{L}_1/\mathbb{K}\), \(\mathbb{L}_2/\mathbb{L}\)이 주어졌다 하자. 그럼 우리는 \(\mathbb{L}_1\)과 \(\mathbb{L}_2\)를 동시에 포함하는 가장 작은 extension을 생각할 수 있다.

정의 7 두 개의 \(\mathbb{K}\)-extension \(\mathbb{L}_1/\mathbb{K}\), \(\mathbb{L}_2/\mathbb{L}\)에 대하여, \(\mathbb{K}\)-extension \(\mathbb{K} \rightarrow \mathbb{M}\)이 이들의 composite이라는 것은 다음의 diagram

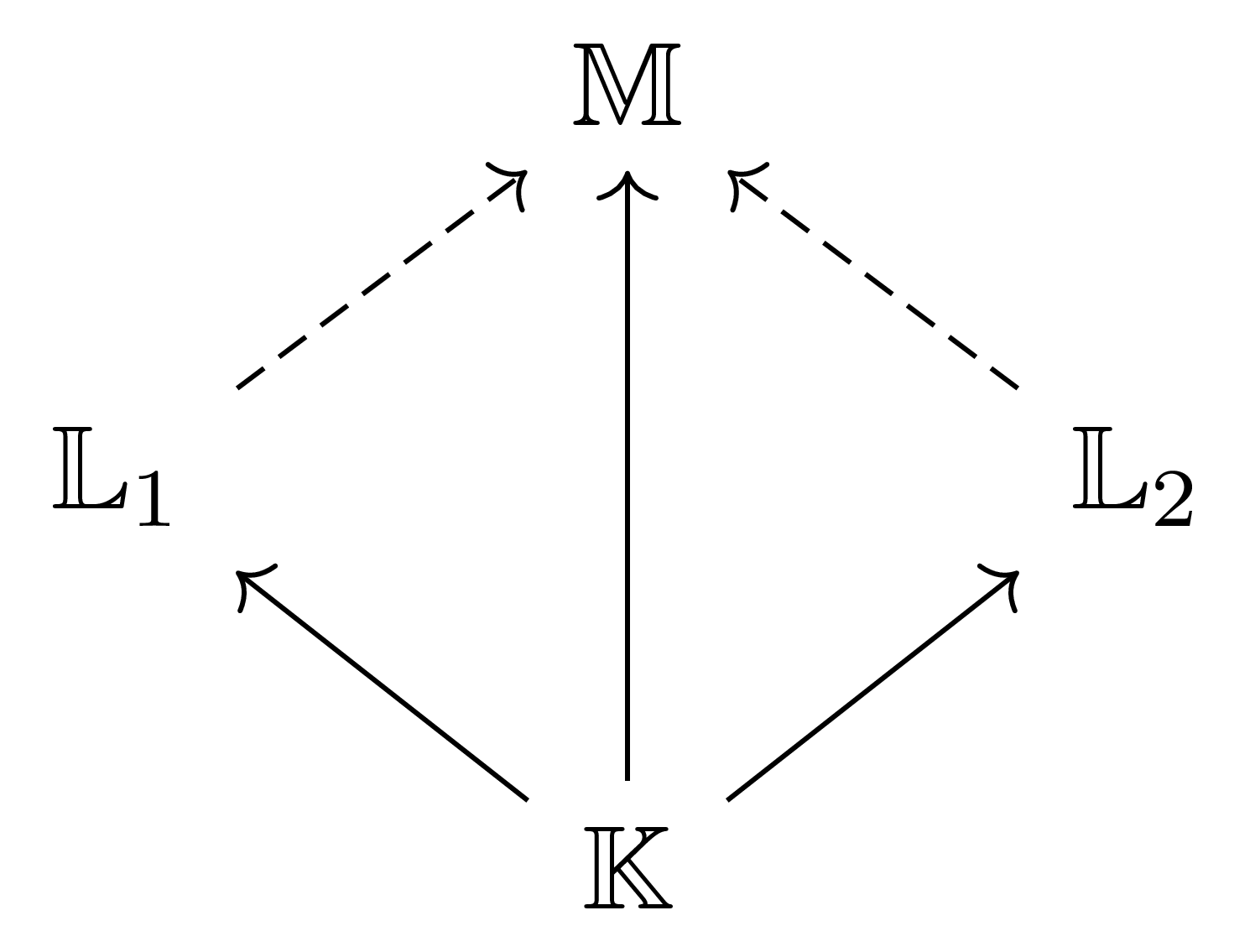
을 commute하도록 하는 \(\mathbb{K}\)-algebra homomorphism \(\mathbb{L}_1 \rightarrow \mathbb{M}\)과 \(\mathbb{L}_2 \rightarrow \mathbb{M}\)이 존재하는 것이다.

이는 구체적으로 다음과 같이 쓸 수 있다.

명제 8 두 \(\mathbb{K}\)-extension \(\mathbb{L}_1, \mathbb{L}_2\)가 주어졌다 하자.

1. 이들의 composite field \(\mathbb{M}\)과 extension \(u_i: \mathbb{L}_i \rightarrow \mathbb{M}\)에 대하여, 다음의 식

   \[\mathbb{L}_1\otimes_\mathbb{K} \mathbb{L}_2 \rightarrow \mathbb{M};\qquad x_1\otimes x_2\mapsto u_1(x_1)u_2(x_2)\]

   으로 정의된 함수 \(u_1\ast u_2: \mathbb{L}_1\otimes_\mathbb{K} \mathbb{L}_2 \rightarrow \mathbb{M}\)의 kernel \(\ker (u_1\ast u_2)\)는 prime ideal이다.

2. 거꾸로, \(\mathbb{L}_1\otimes_\mathbb{K} \mathbb{L}_2\)의 임의의 prime ideal \(\mathfrak{p}\)에 대하여, 적당한 composite field \(\mathbb{M}\)과 extension \(u_i: \mathbb{L}_i \rightarrow \mathbb{M}\)가 존재하여, \(\mathfrak{p}\)가 \(u_1\ast u_2\)의 kernel이도록 할 수 있다.

증명

1. \(u_1\ast u_2\)의 image \(\im(u_1\ast u_2)\)는 field \(\mathbb{M}\)의 subring이고, 따라서 integral domain이다. 이제 주어진 주장은 [대수적 구조] §분수체, ⁋명제 8과 [대수적 구조] §몫환, 환 동형사상, ⁋정리 3으로부터 자명하다.

2. 거꾸로 \(\mathfrak{p}\)가 \(\mathbb{L}_1\otimes_\mathbb{K}\mathbb{L}_2\)의 prime ideal이라 하고, integral domain \((\mathbb{L}_1\otimes\mathbb{K}\mathbb{L}_2)/\mathfrak{p}\)의 field of fraction을 \(\mathbb{M}=\Frac((\mathbb{L}_1\otimes_\mathbb{K}\mathbb{L}_2)/\mathfrak{p})\)라 하자. 그럼 각각의 \(x_1\in \mathbb{L}_1\)과 \(x_2\in \mathbb{L}_2\)에 대하여, \(u_1(x_1)\)을 \(x_1\otimes 1\)의 \(\mathbb{M}\)에서의 image, \(u_2(x_2)\)를 \(1\otimes x_2\)의 \(\mathbb{M}\)에서의 image로 정의하면 이들이 원하는 조건을 만족함을 알 수 있다.

뿐만 아니라, 두 번째 결과에 의해 얻어지는 composite field가 isomorphism에 대하여 유일하게 결정된다는 것 또한 자명하다. 한편, 임의의 두 \(\mathbb{K}\)-extension \(\mathbb{L}_1, \mathbb{L}_2\)에 대하여, \(\mathbb{L}_1\otimes_\mathbb{K} \mathbb{L}_2\)는 항상 prime ideal을 가지므로 ([대수적 구조] §환의 정의, ⁋정리 9) 임의의 두 \(\mathbb{K}\)-extension은 composite field를 갖는다는 것을 확인할 수 있다.

대수적 확장

\(\mathbb{K}\)의 적절한 extension \(\Omega\)를 고정하자. 별다른 말이 없다면 모든 field extension들은 \(\Omega\)의 subextension인 것으로 가정한다.

\(\Omega\)의 임의의 두 \(\mathbb{K}\)-subalgebra \(E,F\)에 대하여, multiplication map \(\mu: E\otimes_\mathbb{K}F \rightarrow \Omega\)를 생각하면 그 image \(G\)는 \(E\cup F\)로 생성되는 \(\Omega\)의 subring이다.

정의 9 위와 같은 상황에서, multiplication map \(\mu: E\otimes_\mathbb{K}F \rightarrow G\)가 isomorphism이라면 \(E\)와 \(F\)가 linearly disjoint라 한다.

어렵지 않게 이는 \(E\)와 \(F\)의 두 \(\mathbb{K}\)-basis \((x_i)_{i\in I}\), \((y_j)_{j\in J}\)가 주어졌을 때, \((x_iy_j)_{i\in I,j\in J}\)가 linearly indepdent가 되는 것과 동치임을 안다.

특별히 \(E,F\)가 \(\mathbb{K}\)-extension인 경우 다음 명제를 얻는다.

명제 10 두 \(\mathbb{K}\)-extension \(\mathbb{L}_1, \mathbb{L}_2\)에 대하여 다음이 성립한다.

1. \(\mathbb{L}_2\)가 finite degree를 가지면, \(\mathbb{L}_1 \cup \mathbb{L}_2\)로 생성되는 \(\Omega\)의 subring은 field가 되며, 이는 \(\mathbb{L}_1(\mathbb{L}_2)\)와 일치한다. 또한 \(\mathbb{L}_1(\mathbb{L}_2)\)의 \(\mathbb{L}_1\)에 대한 degree도 유한하고,

   \[[\mathbb{L}_1(\mathbb{L}_2) : \mathbb{L}_1] \leq [\mathbb{L}_2 : \mathbb{K}]\]

   이며, 등호는 \(\mathbb{L}_1\)와 \(\mathbb{L}_2\)가 linearly disjoint할 때 성립한다. 이 경우, \(\mathbb{L}_1(\mathbb{L}_2)\)는 \(\mathbb{L}_1 \otimes_\mathbb{K} \mathbb{L}_2\)와 \(\mathbb{L}_1\)-isomorphic하다.

2. 위의 조건에 더하여 더 나아가 \(\mathbb{L}_1\)의 degree도 유한하다 가정하자. 그럼 \(\mathbb{L}_1(\mathbb{L}_2) = \mathbb{K}(\mathbb{L}_1 \cup \mathbb{L}_2)\)의 degree 또한 유한하고

   \[[\mathbb{K}(\mathbb{L}_1 \cup \mathbb{L}_2) : \mathbb{K}] \leq [\mathbb{L}_1 : \mathbb{K}][\mathbb{L}_2 : \mathbb{K}]\]

   이며, 등호는 \(\mathbb{L}_1\)와 \(\mathbb{L}_2\)가 linearly disjoint할 때 성립한다.

증명

1. \(\mathbb{L}_1 \cup \mathbb{L}_2\)로 생성되는 \(\Omega\)의 subring을 \(G\)라 하자. 만약 \((y_j)_{1 \leq j \leq n}\)이 \(\mathbb{L}_2\)의 \(\mathbb{K}\)-basis라면, \(G\)는 \(\mathbb{L}_1\)-벡터공간으로서 \(y_j\)들로 생성된다. 그러면 \(G\)는 finite rank \(\leq n\)을 가지는 \(\mathbb{L}_1\)-algebra가 된다. 이제 \(G\)는 field \(\Omega\) 안에 포함되어 있으므로 integral domain이며, 따라서 명제 3에 의하여 field가 된다. 결과적으로 \(G=\mathbb{L}_1(\mathbb{L}_2)\)이고,

   \[[\mathbb{L}_1(\mathbb{L}_2) : \mathbb{L}_1] \leq [\mathbb{L}_2 : \mathbb{K}]\]

   가 성립한다.
   또한 \([\mathbb{L}_1(\mathbb{L}_2) : \mathbb{L}_1] = [\mathbb{L}_2 : \mathbb{K}]\)이면 \(y_j\)들이 \(\mathbb{L}_1\) 위에서 linearly independent여야 한다. 즉, \(\mathbb{L}_1\)와 \(\mathbb{L}_2\)가 linearly disjoint이다.

2. 이는 다음의 식

   \[[\mathbb{L}_1(\mathbb{L}_2) : \mathbb{K}] = [\mathbb{L}_1(\mathbb{L}_2) : \mathbb{L}_1][\mathbb{L}_1 : \mathbb{K}]\]

   에 의하여 자명하다.

일반적으로 두 \(\mathbb{K}\)-extension \(\mathbb{L}_1,\mathbb{L}_2\)에 대하여 ring \(\mathbb{K}[\mathbb{L}_1\cup \mathbb{L}_2]\)는 field가 아님을 앞에서 언급하였다. 그러나 다음의 식

\[\Frac(\mathbb{K}[\mathbb{L}_1\cup\mathbb{L}_2])=\mathbb{K}(\mathbb{L}_1\cup\mathbb{L}_2)\]

이 성립한다. 더 일반적으로, \(S_i\subseteq \mathbb{L}_i\)가 \(\Frac(S_i)=\mathbb{L}_i\)를 만족하는 부분집합들이라 하자. \(G\)를 \(S_1\cup S_2\)로 생성되는 ring이라 하면, 우리는 다음의 isomorphism

\[\Frac(G)\cong \mathbb{K}(\mathbb{L}_1\cup\mathbb{L}_2)\]

을 얻는다. 다음 명제는 이 관찰을 linearly disjoint extension의 언어로 확장한 것이다.

명제 11 두 \(\mathbb{K}\)의 두 extension이라 하고, \(E_1\), \(E_2\)가 \(\Omega\)의 \(\mathbb{K}\)-subalgebra들이라 하자. \(\mathbb{L}_1=\Frac(E_i)\)라 하면, \(\mathbb{L}_1\)와 \(\mathbb{L}_2\)가 linearly disjoint인 것과 \(E_1\)와 \(E_2\)가 linearly disjoint인 것이 동치이다.

증명

한쪽 방향은 자명하므로 \(E_1, E_2\)가 linearly disjoint라 가정하자. 그럼 우선 \(E_1\)과 \(\mathbb{L}_2\)가 linearly disjoint임을 보일 수 있는데, \(\Omega\)의 임의의 \(E_2\)-free family는 \(\mathbb{L}_2\)-free이기도 하기 때문이다. 이제 같은 논리로 \(\mathbb{L}_1\)와 \(\mathbb{L}_2\)가 linearly disjoint이다.

한편, 임의의 family의 linear combination은 (그 family가 무한하더라도) 유한한 합으로만 이루어지므로 다음이 성립한다.

명제 12 두 \(\mathbb{K}\)-extension \(\mathbb{L}_1\), \(\mathbb{L}_2\)를 field \(\mathbb{K}\)을 생각하자. 만약 \(\mathbb{L}_1\)와 \(\mathbb{L}_2\)가 linearly disjoint하다면, \(\mathbb{L}_1\)의 모든 subextension과 \(\mathbb{L}_2\)의 모든 subextension도 \(\mathbb{K}\) 위에서 linearly disjoint하다. 거꾸로 \(\mathbb{L}_i\)들의 모든 finitely generated subextension \(\mathbb{L}_i'\)들에 대해 \(\mathbb{L}_1'\)와 \(\mathbb{L}_2'\)가 linearly disjoint하다면, \(\mathbb{L}_1\)와 \(\mathbb{L}_2\)도 linearly disjoint하다.

즉, 임의의 두 extension이 linearly disjoint인지의 여부는 두 extension의 임의의 finite subextension들만 봐도 확인할 수 있다.

명제 13 세 \(\mathbb{K}\)-extension \(\mathbb{L},\mathbb{M}_1,\mathbb{M}_2\)이 주어졌다 하고, \(\mathbb{M}_1 \subseteq \mathbb{M}_2\)라고 하자. 그럼 \(\mathbb{L}\)과 \(\mathbb{M}_2\)가 linearly disjoint인 것과, \(\mathbb{L}\)와 \(\mathbb{M}_1\)가 linearly disjoint인 동시에 \(\mathbb{L}(\mathbb{M}_1)\)와 \(\mathbb{M}_2\)가 linearly disjoint인 것이 서로 동치이다.

증명

우선 \(\mathbb{L}\)과 \(\mathbb{M}_2\)가 linearly disjoint하다고 가정하자. 그럼 명제 12에 의하여 \(\mathbb{L}\)와 \(\mathbb{M}_1\)도 linearly disjoint이다. 한편, \(\mathbb{L}\)의 \(\mathbb{K}\)-basis는 \(\mathbb{M}_1[\mathbb{L}]\)의 \(\mathbb{M}_1\)-basis이기도 하다. 그런데 가정에 의해 이 basis는 \(\mathbb{M}_2\)-free이므로, \(\mathbb{M}_1[\mathbb{L}]\)와 \(\mathbb{M}_2\)는 linearly disjoint이다. 또, 명제 11에 의해 \(\mathbb{L}(\mathbb{M}_1) = \mathbb{M}_1(\mathbb{L})\)와 \(\mathbb{M}_2\) 역시 linearly disjoint하다.

이제 반대방향을 보이자. 위에서와 마찬가지로 \(\mathbb{L}\)의 \(\mathbb{K}\)-basis \(B\)를 생각하면, 가정으로부터 \(B\)는 \(\mathbb{M}_1\)-free이다. 따라서 \(B\)는 \(\mathbb{M}_1[\mathbb{L}]\)의 \(\mathbb{M}_1\)-basis이며, 다시 가정에 의해 \(\mathbb{M}_1[\mathbb{L}]\)와 \(\mathbb{M}_2\)는 linearly disjoint이므로 원하는 결과를 얻는다.

Field \(\mathbb{K}\), \(\mathbb{K}\)-algebra \(E\)를 생각하자. 그럼 임의의 \(x\in E\)에 대하여, 다음 둘 중 정확히 하나가 성립한다.

1. \((x^n)_{n\geq 0}\)이 \(\mathbb{K}\)-free이다.
2. \(1,x,\cdots, x^{n-1}\)이 \(\mathbb{K}\)-linearly dependent이도록 하는 \(n\)이 존재한다.

정의 14 위와 같은 상황에서, 만일 첫 번째 경우가 성립한다면 \(x\in E\)가 transcendental_초월적이라 부르고, 두 번째 경우가 성립한다면 \(x\)를 algebraic_대수적이라 부른다.

이제 \(x\in E\)가 algebraic이라 하자. 그럼 \(1,x,\ldots, x^{n-1}\)이 \(\mathbb{K}\)-linearly dependent이도록 하는 \(n\) 중 가장 작은 것을 \(x\)의 degree_차수라 하고, 이 때의 linear combination

\[a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0=0\]

에 대하여, 다음의 다항식

\[f(\x)=\x^n-\sum_{k=0}^{n-1}\frac{a_k}{a_n}\x^k\]

을 \(x\)의 minimal polynomial_{최소다항식}이라 부른다.

그럼 다음 정리가 성립하며, 그 증명 또한 그렇게 어렵지 않다.

정리 15 \(\mathbb{K}\)-algebra \(E\)의 algebraic element \(x\in E\)에 대하여, \(x\)의 degree를 \(n\), minimal polynomial을 \(f\)라 하자. 그럼 다음이 성립한다.

1. \(g \in \mathbb{K}[\x]\)에 대해 \(g(x) = 0\)이 되기 위한 필요충분조건은 \(g\)가 \(f\)의 배수인 것이다.
2. \(\mathbb{K}[\x] \rightarrow \mathbb{K}[x]\)를 \(g\mapsto g(x)\)로 정의하자. 그럼 이 morphism은 quotient algebra \(\mathbb{K}[\x]/(f)\)로 factor through하며, 그 결과로 얻어지는 \(\mathbb{K}[\x]/(f) \rightarrow \mathbb{K}[x]\)는 isomorphism이다. 또, 이 때 \(1, x, \dots, x^{n-1}\)은 \(\mathbb{K}[x]\)의 \(\mathbb{K}\)-basis를 이루며, 따라서 \([\mathbb{K}[x] : \mathbb{K}] = n\)이 성립한다.
3. 만일 \(E\)가 integral domain이라면 \(\mathbb{K}[x]\)는 field이며, \(f\in \mathbb{K}[\x]\)는 \(f(x) = 0\)를 만족하는 유일한 monic irreducible polynomial이다.
4. \(x\)가 \(E\)에서 invertible element가 되기 위한 필요충분조건은 \(f(0) \neq 0\)인 것이며, 이 때 \(x^{-1} \in \mathbb{K}[x]\)이다.

또, extension \(\mathbb{K}\hookrightarrow \mathbb{L}\)과 \(\mathbb{L}\)-algebra \(E\)에 대하여, 원소 \(x\in E\)가 \(\mathbb{K}\)에 대해 algebraic이라면, \(x\)는 \(\mathbb{L}\)에 대해서도 algebraic이며 그 degree는 \(\mathbb{K}\)에 대한 degree를 넘지 못한다는 것을 안다.

정의 16 모든 원소가 algebraic인 field extension \(\mathbb{L}/\mathbb{K}\)를 algebraic extension_{대수적 확장}이라 부른다. 그렇지 않은 field extension은 transcendental extension_{초월적 확장}이라 부른다.

그럼 어렵지 않게 extension \(\mathbb{L}/\mathbb{K}\)가 algebraic인 것은 \(\mathbb{L}\)의 임의의 \(\mathbb{K}\)-subalgebra가 field인 것과 동치임을 알 수 있다. 또, 다음 명제가 자명하다.

명제 17 Degree \(n\) \(\mathbb{K}\)-extension \(\mathbb{L}\)은 반드시 algebraic extension이며, \(\mathbb{L}\)의 임의의 원소의 degree는 \(n\)의 약수이다.

증명

\[[\mathbb{L}:\mathbb{K}]=[\mathbb{L}:\mathbb{K}(x)][\mathbb{K}(x):\mathbb{K}].\]

이를 귀납적으로 확장하면 다음을 얻는다.

정리 18 Finitely generated \(\mathbb{K}\)-extension \(\mathbb{L}\)이 algebraic element들 \(a_1, \dots, a_m\)에 의해 생성된다고 하자. 그럼 \(\mathbb{L}/\mathbb{K}\)는 finite degree extension이다. 뿐만 아니라, 만일 각각의 \(i\)에 대하여 \(a_i\)의 \(\mathbb{K}(a_1, \dots, a_{i-1})\) 위에서의 degree를 \(n_i\)라 하면, \(\mathbb{L}\)의 \(\mathbb{K}\)에 대한 degree는 \(n_1 n_2 \cdots n_m\)이며, 다음의 원소들

\[a_1^{\nu_1} a_2^{\nu_2} \cdots a_m^{\nu_m}\qquad (0 \leq \nu_i \leq n_i - 1)\]

이 \(\mathbb{L}\)의 \(\mathbb{K}\)-basis가 된다.

특히 algebraic element들로만 이루어진 집합 \(A\)에 대해서는 \(\mathbb{K}(A)=\mathbb{K}[A]\)가 성립한다. 뿐만 아니라, algebraic extension은 transitive하다. 즉, 다음 명제가 성립한다.

명제 19 Field extension \(\mathbb{M}/\mathbb{L}/\mathbb{K}\)에 대하여, \(\mathbb{M}\)이 \(\mathbb{K}\)에 대해 algebraic하기 위한 필요충분조건은 \(\mathbb{L}\)가 \(\mathbb{K}\)에 대해 algebraic한 동시에 \(\mathbb{M}\)이 \(\mathbb{L}\)에 대해 algebraic한 것이다.

증명

한쪽 방향은 자명하므로, 역만 보이면 충분하다. \(\mathbb{L}\)가 \(\mathbb{K}\)에 대해 algebraic한 동시에 \(\mathbb{M}\)이 \(\mathbb{L}\)에 대해 algebraic하다고 가정하고, \(\mathbb{M}\)의 임의의 원소 \(x\)를 잡자. 우리는 \(x\)가 \(\mathbb{K}\)에 대해 algebraic임을 보여야 한다.

우선 가정에 의해 \(x\)는 \(\mathbb{L}\) 위에서 algebraic하다. \(g \in \mathbb{L}[\x]\)를 \(x\)의 minimal polynomial이라 하고, \(g\)의 계수들의 집합을 \(A\)라 하자. 그러면 \(g \in \mathbb{K}(A)[\x]\)가 되고, 따라서 \(x\)는 \(\mathbb{K}(A)\) 위에서 algebraic하다.

또한 \(\mathbb{K}(A \cup \{x\}) = \mathbb{K}(A)(x)\)는 \(\mathbb{K}(A)\) 위에서 finite degree를 가진다. \(A \subseteq \mathbb{L}\)이고, \(\mathbb{L}\)가 \(\mathbb{K}\) 위에서 algebraic이므로 정리 18에 의해 \(\mathbb{K}(A)\)는 \(\mathbb{K}\) 위에서 finite degree를 가진다. 이로부터 \(\mathbb{K}(A \cup \{x\})\)는 \(\mathbb{K}\) 위에서 finite degree를 가지고, 따라서 \(x\)가 \(\mathbb{K}\)에 대해 algebraic이다.