이제 우리는 \(\Ch(\mathcal{A})\)에서의 short exact sequence가 long exact sequence를 유도한다는 것을 보인다.
긴 완전열
우리는 앞서 chain map \(f_\bullet\)의 image와 kernel이 각각의 \(f_n\)의 image와 kernel로 이루어진 chain complex가 된다는 것을 보았다. 따라서
\[0\rightarrow A_\bullet\rightarrow B_\bullet\rightarrow C_\bullet\rightarrow 0\]이 short exact sequence라는 것은 모든 \(n\)에 대하여
\[0\rightarrow A_n\rightarrow B_n\rightarrow C_n\rightarrow 0\]이 short exact sequence라는 것과 동치라는 것을 확인할 수 있다.
이번 글의 가장 큰 정리는 다음의 정리 1이다. 이 때 증명에서 snake lemma가 중요한 역할을 하며, 또 카테고리가 \(\lMod{A}\)인 경우에 명시적으로 얻어지는 connecting map을 이용하면 증명을 쉽게 마칠 수 있으므로, §Diagram chasing에서와 마찬가지로 Freyd-Mitchell embedding theorem을 적극적으로 이용하여 \(\lMod{A}\)에서 다음 정리에 대한 증명을 진행한다.
정리 1 (The long exact sequence) 다음의 short exact sequence
\[0\rightarrow A_\bullet\rightarrow B_\bullet\rightarrow C_\bullet\rightarrow 0\]가 주어졌다 하자. 그럼 호몰로지들 사이의 long exact sequence
\[\cdots\rightarrow H_n(A)\rightarrow H_n(B)\rightarrow H_n(C)\rightarrow H_{n-1}(A)\rightarrow \cdots\]가 존재한다.
증명
이는 다음의 diagram
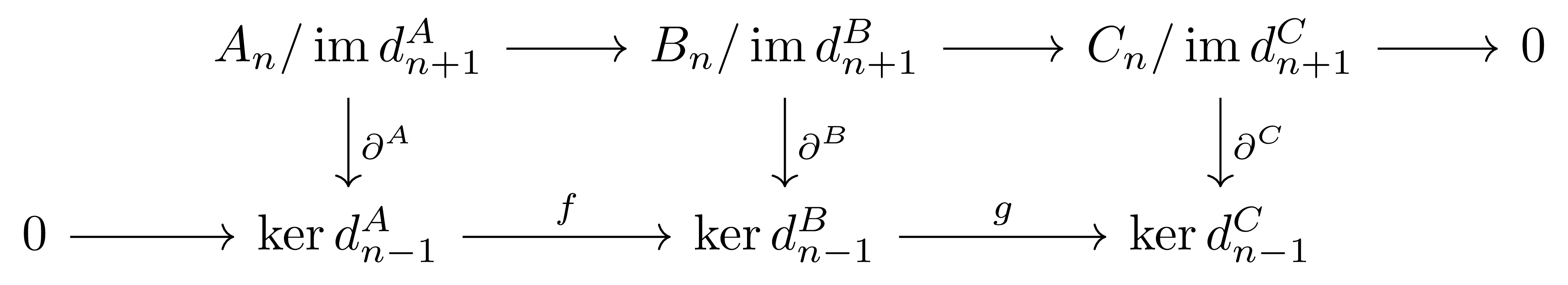
을 생각하면 된다. 여기에서 \(\partial\)들은 모두 \(\partial^A(a+\im d^A_{n+1})=d_n^Aa\in\ker d^A_{n-1}\)과 같이 정의된 함수들이다. 그럼 위의 diagram에서 \(\ker\partial^A\)는 \(H_{n+1}(A)=\ker d_n^A/\im(d^A_{n+1})\)와 같고, \(\coker\partial^A\)는 \(H_{n-1}(A)=\ker d^A_{n-1}/\im d^A_n\)과 같다는 것을 쉽게 확인할 수 있다.
따라서, 위와 아래의 행이 모두 exact라는 것만 보인다면, snake lemma에 의해 주어진 long exact sequence가 잘 유도된다. 이를 보이기 위해 다시 다음의 diagram
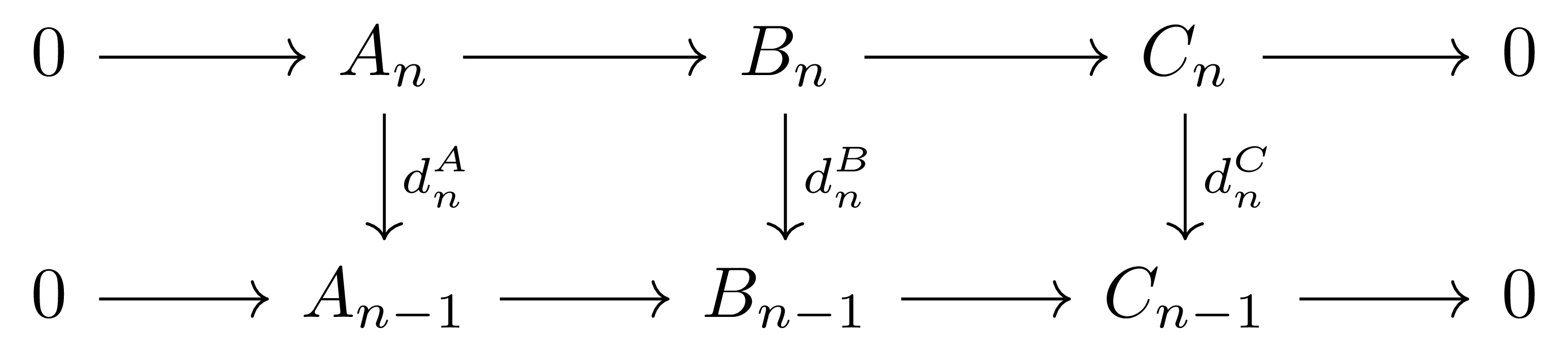
을 생각하자. 이 diagram에 snake lemma (더 정확하게는 §Diagram chasing, ⁋보조정리 5) 를 다시 한 번 적용하면, 두 exact sequence
\[0\rightarrow \ker(d_n^A)\rightarrow \ker(d_n^B)\rightarrow \ker(d_n^C)\]그리고
\[\coker(d_n^A)\rightarrow\coker(d_n^B)\rightarrow\coker(d_n^C)\rightarrow 0\]이 얻어진다.
위에서 만든 long exact sequence는 다음과 같은 센스에서 functoriality를 가진다.
명제 2 두 short exact sequence들 사이의 chain map
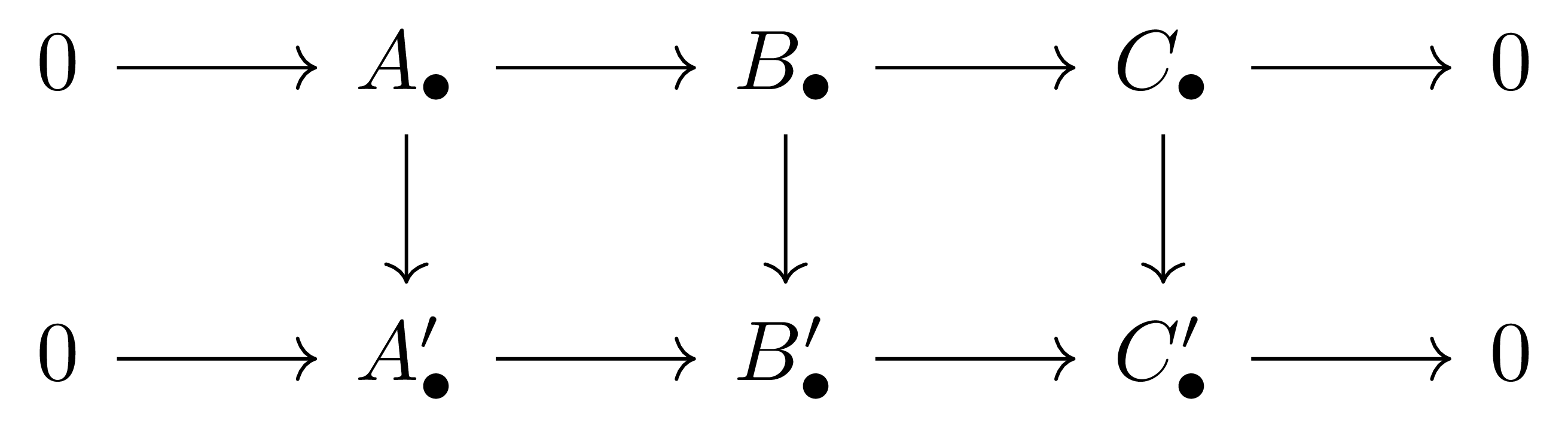
이 주어졌다 하면, 이에 대응하는 long exact sequence들 사이의 chain map
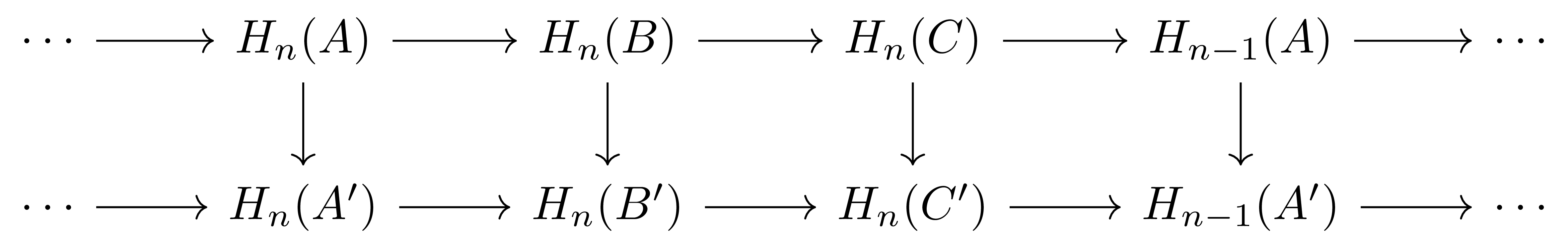
이 존재한다.
증명
유사동형인 사슬복합체
지금까지 살펴본 chain complex들 사이의 isomorphism을 어떻게 정의해야 하는지는 명확하다.
정의 3 두 chain complex \(C_\bullet\), \(D_\bullet\)이 주어졌다 하자. 그럼 \(C_\bullet\)과 \(D_\bullet\)이 isomorphic하다는 것은 임의의 두 chain map \(f:C_\bullet\rightarrow D_\bullet\), \(g:D_\bullet\rightarrow C_\bullet\)이 존재하여 \(fg=\id_D\)이고 \(gf=\id_C\)인 것이다. 이 때, \(f,g\)를 두 chain complex 사이의 isomorphism이라 부른다.
이는 곧, 각각의 \(f_n\)들이 모두 isomorphism인 chain map \((f_n)_{n\in\mathbb{Z}}\)이 존재한다는 것과 동치이다.
한편 호몰로지 대수학에서 우리가 사용할 수 있는 도구는 호몰로지 뿐이므로, 다음과 같이 동형사상의 개념을 약화시킬 수 있다.
정의 4 두 chain complex \(C_\bullet\), \(D_\bullet\)이 quasi-isomorphic유사동형하다는 것은 모든 \(n\)에 대하여 \(H_n(C)\cong H_n(D)\)인 것이다. 만일 어떤 chain map \(f:C\rightarrow D\)과 모든 \(n\)에 대해 \(H_n(f)\)가 isomorphism이 된다면, \(f\)를 quasi-isomorphism유사동형사상이라 부른다.1
정의에 의해 isomorphic한 두 chain complex들은 quasi-isomorphic하기도 하다. 그러나 그 역은 성립하지 않는다. 모든 성분이 0인 sequence
\[\cdots\rightarrow 0\rightarrow 0\rightarrow 0\rightarrow\cdots\]와 isomorphic한 chain complex는 자기자신 뿐이지만, 임의의 exact sequence는 항상 모든 homology module이 0이 된다.
사슬 호모토피
한편, 두 개의 chain complex의 동치관계를 위와 같이 quasi-isomorphism으로 약화시킨다면, 마찬가지 논리로 두 chain map이 각각의 호몰로지에서 같은 함수를 정의한다면 이들 또한 같은 것으로 취급하는 것이 조금 더 타당할 것이다. 이를 위해 다음을 정의한다.
정의 5 두 chain complex \(C,D\)와 chain map \(f,g:C\rightarrow D\)가 주어졌다 하자. 그럼 \(f\)와 \(g\) 사이의 chain homotopy사슬 호모토피은 다음 diagram
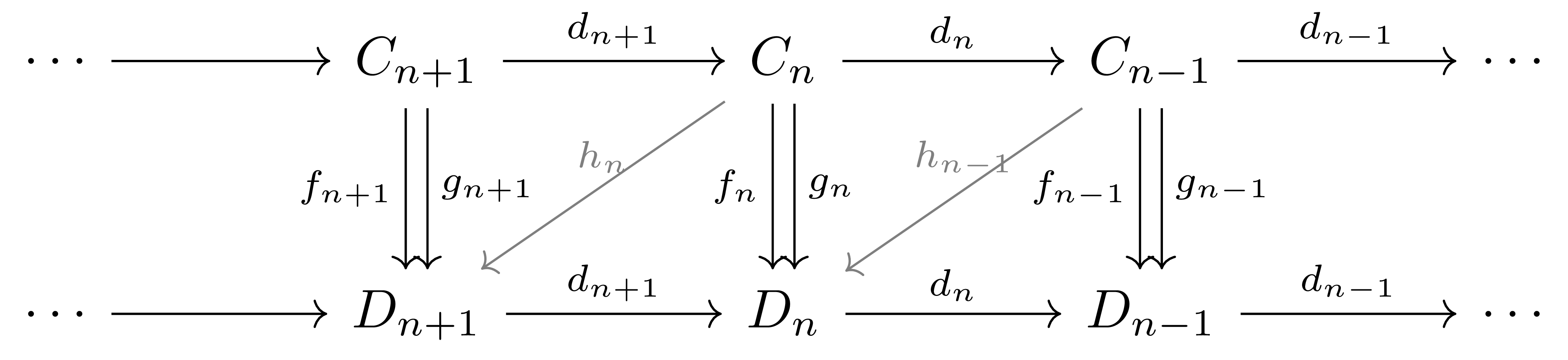
에서, \(f_n-g_n=d_{n+1}^Dh_n+h_{n-1}d_n^C\)가 성립하도록 하는 \(h_n:C_n\rightarrow D_{n+1}\)의 모임이다. 만일 \(f,g\) 사이의 chain homotopy가 존재한다면, \(f\)와 \(g\)가 homotopic한 chain map이라 부른다.
만일 어떤 chain map \(f\)에 대하여, \(f=dh+hd\)를 만족하는 \(h\)가 존재한다면, \(h\)를 \(f\)와 \(0\) 사이의 chain homotopy로 볼 수 있다. 따라서 이와 같은 \(h\)가 존재할 경우 \(f\)를 null homotopic하다 부른다.
명제 6 두 homotopic chain map \(f,g:C\rightarrow D\)는 homology들 위에서 같은 함수를 유도한다.
증명
임의의 \([a]\in H_n(C)=\ker(d^C_{n})/\im(d^C_{n+1})\)을 택하고, \(a\in\ker(d_{n}^C)\)가 representative라 하자. 우리는
\[f_n(a)-g_n(b)\in\im(d_{n+1}^D)\]을 보여야 한다. 그런데 다음의 식
\[(d_{n+1}^D\circ h_n)(a)+(h_{n-1}\circ d_n^C)(a)=f_n(a)-g_n(a)\]으로부터, \(a\in \ker(d_n^C)\)이므로
\[f_n(a)-g_n(a)=d_{n+1}^D)(h_n(a))\in\im(d_{n+1}^D)\]을 얻는다.
만일 어떤 chain map \(f:C\rightarrow D\)에 대하여, 적당한 chain map \(g:D\rightarrow C\)가 존재하여 \(gf\)가 \(\id_C\)와 homotopic하고, \(fg\)가 \(\id_D\)와 homotopic하다면 \(f\)를 chain homotopy equivalence라 부른다.
Homotopy category
명제 6에 힘입어, 우리는 homotopy category \(\mathbf{K}(\mathcal{C})\)를 다음 과정을 통해 정의할 수 있다. 우선 다음의 첫 번째 보조정리는 자명하다.
보조정리 7 두 chain map 사이의 homotopy relation은 동치관계다.
이를 통해 \(\Hom_{\mathbf{Ch}(\mathcal{C})}(C_\bullet,D_\bullet)\) 위에 동치관계를 정의할 수 있다. 이 동치관계에 의해 생긴 quotient set을 \(\Hom_{\mathbf{K}(\mathcal{C})}(C_\bullet,D_\bullet)\)으로 정의하자.
\(\mathbf{K}(\mathcal{C})\)는 \(\mathbf{Ch}(\mathcal{C})\)와 동일한 object를 갖고, 이들 사이의 morphism들의 집합은 위와 같이 정의된 \(\Hom_{\mathbf{K}(\mathcal{C})}\)와 같고, 이 집합이 abelian group의 구조를 갖는다는 것을 확인할 수 있다.
두 homotopic chain map \(f,g:C\rightarrow D\)가 주어졌다 하자. 임의의 \(u:B\rightarrow C\), \(v:D\rightarrow E\)에 대하여 두 map \(vfu\)와 \(vgu\)를 생각하자. 다음 diagram
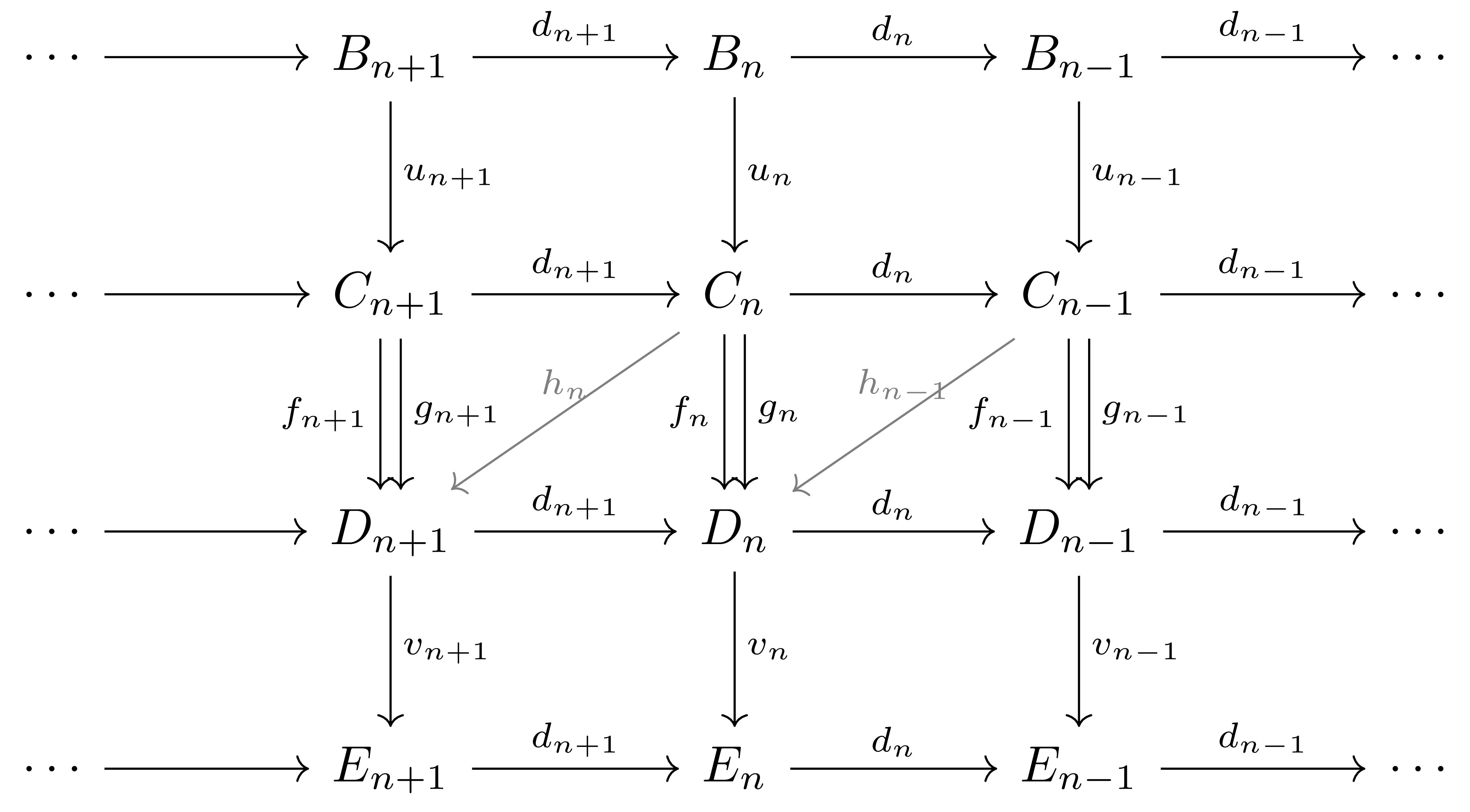
을 생각하면,
\[\begin{aligned}v_nf_nu_n-v_ng_nu_n&=v_n(f_n-g_n)u_n\\&=v_n(d_{n+1}h_n+h_{n-1}d_n)u_n\\&=d_{n+1}v_{n+1}h_nu_n+v_nh_{n-1}u_{n-1}d_n\end{aligned}\]이 되어, \(vfu\)와 \(vgu\) 사이에 chain homotopy
\[(h'_n=v_{n+1}h_nu_n)_{n\in\mathbb{Z}}\]이 존재한다는 것을 안다. 즉 위에서 정의한 동치관계는 \(\mathbf{Ch}(\mathcal{C})\)의 합성과도 잘 맞아 떨어진다.
비슷한 논리로 \(\mathbf{K}(\mathcal{C})\)가 additive category라는 것을 보일 수 있으며, 자명한 functor \(\mathbf{Ch}(\mathcal{C})\rightarrow\mathbf{K}(\mathcal{C})\)가 additive functor가 된다.
그러나 일반적으로 \(\mathbf{K}(\mathcal{C})\)는 abelian category가 되지는 않는다.
Mapping cone
정의 4에서, 우리는 isomorphic한 homology를 갖는 chain complex들을 quasi-isomorphic하다 부르고, 이들을 같은 것으로 취급하기로 하였다. Mapping cone은 chain map \(f:C_\bullet \rightarrow D_\bullet\)이 주어졌을 때 이것이 quasi-isomorphism인지를 판별하는 도구가 된다.
정의 8 임의의 chain map \(f:C_\bullet\rightarrow D_\bullet\)에 대하여, \(f\)의 mapping cone \(\cone(f)\)는 다음의 chain complex
\[\cdots\longrightarrow\underbrace{C_n\oplus D_{n+1}}_{\cone(f)_{n+1}}\overset{d_{n+1}}{\longrightarrow}\underbrace{C_{n-1}\oplus D_n}_{\cone(f)_n}\overset{d_n}{\longrightarrow}\underbrace{C_{n-2}\oplus D_{n-1}}_{\cone(f)_{n-1}}\longrightarrow\cdots\]를 의미한다. 이 때, differential은 다음의 식
\[d_n(x,y)=(-d_{n-1}(x), d_n(y)-f_{n-1}(x))\qquad (x\in C_{n-1},y\in D_n)\]으로 주어진다.
Chain map \(f: C_\bullet \rightarrow D_\bullet\)이 주어졌다 하고, \(f\)의 mapping cone \(\cone(f)\)에 대하여, chain complex들의 sequence
\[0 \longrightarrow D \longrightarrow \cone(f) \overset{\delta}{\longrightarrow} C[-1] \longrightarrow0\]을 생각하자. 여기서 \(D \rightarrow\cone(f)\)는 \(y\)를 \((0,y)\)로 보내고, \(\delta\)는 \((x,y)\)를 \(-x\)로 보낸다. 그럼 이 함수들의 정의에 의하여 위의 sequence가 short exact sequence가 되는 것이 자명하므로, 정리 1에 의하여 다음의 long exact sequence
\[\cdots \rightarrow H_{n+1}(\cone(f)) \rightarrow H_n(B) \rightarrow H_n(C) \rightarrow H_n(\cone(f)) \rightarrow H_{n-1}(B) \rightarrow \cdots\]가 존재한다. 한편 이 정리의 증명을 뜯어보면, 위에서 얻어지는 connecting map \(H_n(B) \rightarrow H_n(C)\)들이 정확히 \(H_n(f)\)가 되는 것을 알 수 있다. 따라서 다음이 성립한다.
따름정리 9 Chain map \(f: C_\bullet \rightarrow D_\bullet\)이 quasi-isomorphism인 것은 \(\cone(f)\)가 exact sequence인 것과 동치이다.
참고문헌
[Wei] C.A. Weibel. An Introduction to Homological Algebra. Cambridge Studies in Advanced Mathematics. Cambridge University Press, 1995.
-
접두사 quasi-의 적절한 변역은 준-인 것으로 보이는데, quasi-isomorphism의 경우 homomorphism이 이미 준동형사상이라는 번역을 사용하고 있으므로 별수없이 유사동형사상이라는 이름을 새로 사용했다. ↩

댓글남기기