스킴의 성질들

위상적 성질들

스킴은 위상공간이므로, 위상공간으로서의 성질애 대한 이야기를 할 수 있다. 다만 여기에는 하나의 예외가 있는데, compactness가 그것이다.

예시 1 임의의 affine scheme $\Spec A$를 생각하자. 그럼 $\Spec A$의 임의의 open covering $(U_i)$에 대하여, $U_i=\bigcup_{j\in J_i} D(f_{ij})$이도록 하는 $f_{ij}\in A$가 존재한다. 그럼

\[\Spec A=\bigcup_{i,j}D(f_{ij})\iff A=\sum_{i,j} (f_{ij})\]

인 것으로부터 $1\in\sum_{i,j}(f_{ij})$이고, 따라서 $1$은 오직 유한 개의 $f_{ij}$들의 일차결합으로 표현할 수 있다. 이 표현에서 등장하는 $D(f_{ij})$들이 $\Spec A$를 덮는다.

즉, 임의의 affine scheme은 [위상수학] §옹골공간, ⁋정의 1의 정의에 따르면 compact인 위상공간이다. 그런데 이는 기하적인 직관과는 다소 차이가 있는데, 가령 $\Spec \mathbb{k}[\x]$는 우리의 기하학적 직관에 따르면 수직선이고, 따라서 이것이 compact인 것은 직관적으로 어색하다.

정의 2 Scheme $X$가 위상공간으로서 compact라면, 이를 quasi-compact scheme이라 부른다. Scheme $X$가 위상공간으로서 compact, Hausdorff space라면 이를 compact scheme이라 부른다.

그 외의 경우에는 connected scheme, irreducible scheme, Noetherian scheme 등과 같은 것을 위상공간의 성질로 정의한다. 즉, 표기의 편의상 scheme $X$에 대하여 $X$를 위상공간으로 본 것을 $\lvert X\rvert$로 표기하면 $X$에 위상적 성질을 정의하는 것은 다음과 같은 형태가 된다.

정의 3 Scheme $X$가 connected인 것은 $\lvert X\rvert$가 connected인 것이다. 비슷하게, $X$가 irreducible인 것은 $\lvert X\rvert$가 irreducible인 것이다.

예컨대 $\mathbb{A}^n_\mathbb{k}$와 $\mathbb{P}^n_k$는 irreducible이다.

Connected가 아닌 scheme의 예시는 $\mathbb{A}^1_\mathbb{k}$의 (closed) subscheme

\[\Spec \frac{\mathbb{k}[\x]}{(\x(\x-1))}\]

이 있으며, connected이지만 irreducible하지 않은 scheme의 예시로는

\[V(\x\y)=\Spec \frac{\mathbb{k}[\x,\y]}{(\x\y)}\]

이 있다.

대수적 성질들

한편 $X$는 대수적인 대상이기도 하므로, 대수적인 성질들을 정의할 수도 있다.

정의 4 Scheme $X$가 reduced인 것은 임의의 열린집합 $U$에 대하여 $\mathscr{O}_X(U)$가 reduced인 것이다. 비슷하게, $X$가 integral인 것은 임의의 열린집합 $U$에 대하여 $\mathscr{O}_X(U)$가 integral domain인 것이다. ([대수적 구조] §분수체, ⁋정의 11)

Non-reduced scheme의 예시로는 $\mathbb{A}^2_\mathbb{k}$의 두 subscheme

\[V(\y-\x^2)=\Spec \frac{\mathbb{k}[\x,\y]}{(\y-\x^2)},\quad V(\y)=\Spec\frac{\mathbb{k}[\x,\y]}{(y)}\]

이 있다.

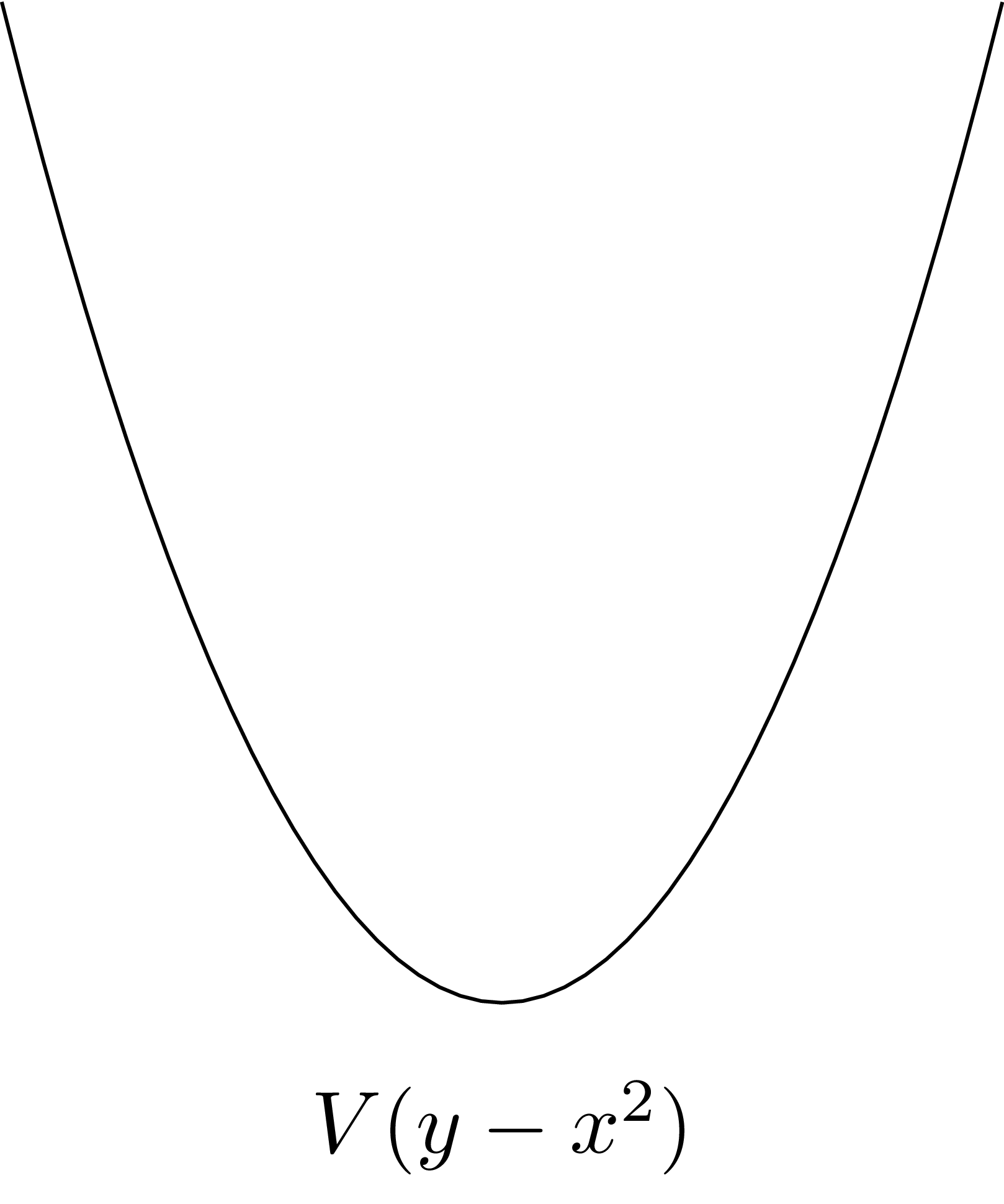
이는 대수적으로는

\[\mathbb{k}[\x,\y]/(\y-\x^2)\cong \mathbb{k}[\x]/(\x^2)\]

이므로, $\x$가 nilpotent element이기 때문이다. 다음 명제는 $X$가 reduced scheme인지의 여부는 stalk에서 확인하는 것으로 충분하다는 것을 보여준다.

명제 5 Scheme $X$가 reduced인 것과 임의의 $x$에 대하여, $\mathscr{O}_{X,x}$가 reduced인 것이 동치이다.

증명

우선 reduced scheme $X$의 임의의 점 $x\in X$에 대하여, $x$를 포함하는 affine open subscheme $U=\Spec A$를 생각하자. $\Spec A$ 안에서 $x$에 대응되는 prime ideal을 $\mathfrak{p}$라 하면

\[\mathscr{O}_{X,x}=(\mathscr{O}_X\vert_U)_x\cong \mathscr{O}_{\Spec A, \mathfrak{p}}\cong A_\mathfrak{p}\]

이고, 가정에 의해 $\mathscr{O}_X(U)\cong A$가 reduced이므로 $A_\mathfrak{p}$ 또한 reduced이다.

거꾸로 임의의 $x\in X$에 대하여 $\mathscr{O}_{X,x}$가 reduced라 하면, 임의의 열린집합 $U$에 대하여 다음 inclusion

\[\mathscr{O}_X(U)\hookrightarrow\prod_{x\in U} \mathscr{O}_{X,x}\]

을 생각하면 $\mathscr{O}_X(U)$가 reduced인 것을 확인할 수 있다.

특히 위의 증명과정에서 임의의 affine scheme $\Spec A$가 reduced인 것과 $A$가 reduced인 것이 동치이다.

명제 7은 대수적으로 정의한 성질들과 위상적으로 정의한 성질들이 서로 관계되어 있다는 점에서 흥미롭다. 이에 대한 증명을 위해서는 다음 보조정리를 먼저 보이는 것이 쓸만하다.

보조정리 6 Affine scheme $\Spec A$가 irreducible인 것은 nilradical $\mathfrak{N}(A)$가 prime ideal인 것과 동치이다.

증명

$\Spec A$가 irreducible인 것은 이 공간의 임의의 두 basis $D(f),D(g)\neq\emptyset$에 대하여 $D(fg)\neq\emptyset$인 것과 동치이다. 그런데 다음 동치관계

\[D(f)\neq\emptyset\iff f\not\in \mathfrak{p}\text{ for some $\mathfrak{p}$}\iff f\not\in \mathfrak{N}(A)\]

로부터, ([대수적 구조] §분수체, ⁋명제 14) 명제 $D(f),D(g)\neq\emptyset\implies D(fg)\not\in\emptyset$은 다음 명제

\[f,g\not\in \mathfrak{N}(A)\implies fg\not\in \mathfrak{N}(A)\]

와 동치임을 안다.

명제 7 $X$가 integral인 것과, $X$가 reduced, irreducible인 것이 동치이다.

증명

우선 $X$가 integral이라 하자. 임의의 integral domain은 항상 reduced이므로 $X$는 reduced scheme이다. 만일 $X$가 irreducible scheme이 아니라 하면, 서로소인 두 열린집합 $U_1,U_2\neq\emptyset$가 존재한다. 그럼 이제 $\mathcal{O}(U_1\cup U_2)=\mathcal{O}(U_1)\times \mathcal{O}(U_2)$가 되어 $X$가 integral이라는 가정에 모순이 된다.

반대로 $X$가 reduced이고 irreducible이라 가정하고, $X$가 integral scheme임을 보이자. 이를 위해서 우리는 임의의 affine open subset $U$에 대해 $\mathcal{O}(U)$가 integral임을 보인다. 우선 $A=\mathcal{O}(U)$는 가정에 의해 reduced이고, $U=\Spec A$는 irreducible space의 열린집합이므로 irreducible이고, 따라서 $\mathfrak{N}(A)=0$가 prime ideal이다. 즉 $\mathcal{O}(U)$가 integral이다.

이제 임의의 열린집합 $V\subseteq X$를 생각하면, scheme의 정의에 의하여 적당한 affine open subset $U\subseteq V$가 존재하고, 따라서 restriction map $\rho_{VU}:\mathcal{O}(V) \rightarrow \mathcal{O}(U)$이 존재한다. 그럼 $\rho_{VU}$는 injective이고, integral domain의 subring은 integral이므로 $\mathcal{O}(V)$가 integral domain이 된다.

따라서 증명을 완료하기 위해서는 $\rho_{VY}$가 injective임을 보이면 충분하다. $f\in\ker\rho_{VU}$라 하자. $f=0$임을 보이기 위해서는 $V$에 속하는 임의의 다른 affine open subset $W$에 대하여 $f$가 $W$에서 $0$이 됨을 보이면 충분하다. 그런데 $\mathcal{O}(W)$는 앞서 증명한 것에 의해 integral이고, $f$가 $U\cap W$에서 $0$이므로 $f$는 $W$에서 $0$이 되어야 한다.

이제 다음을 정의하자.

정의 8 Scheme $X$가 normal이라는 것은 임의의 stalk $\mathscr{O}_{X,x}$가 normal domain인 것이다. ([가환대수학] §정수적 확장, ⁋정의 3) 비슷하게, scheme $X$가 factorial이라는 것은 임의의 stalk $\mathscr{O}_{X,x}$가 unique factorization domain인 것이다.

그럼 factorial scheme은 normal scheme이고, normal scheme은 integral scheme인 것이 자명하다.

Local properties

앞서 reducedness는 stalk-local property였는데, 이 단어에 대한 일반적인 정의는 다음과 같다.

정의 9 Scheme $X$가 주어졌다 하자.

1. $X$에 대한 성질 $P$가 stalk-local이라는 것은, $X$가 $P$를 만족하는 것과 임의의 $x\in X$에 대하여 $\mathscr{O}_{X,x}$가 적당한 성질 $Q$를 만족하는 것이 동치인 것이다.
2. $X$에 대한 성질 $P$가 affine-local이라는 것은, $X$가 $P$를 만족하는 것과 임의의 affine open subset $U$에 대하여 $\mathscr{O}_X(U)$가 적당한 성질 $R$을 만족하는 것이 동치인 것이다.

그럼 reducedness는 stalk-local property이자 affine-local property이다. 일반적으로 임의의 stalk-local property는 affine-local property임이 자명하다. 그러나 다소 유의할 점은 이러한 상황에서 stalk-local property를 affine-local property로 볼 때, 이 성질이 그대로 옮겨가지는 않을 수도 있다는 것이다. 가령 normality는 stalk-local property이므로 affine-local property이기는 하지만, 앞서 살펴보았던 $\Spec \mathbb{k}[\x]/(x(x-1))$을 생각하면 이는 normal subscheme이지만 $\mathbb{k}[\x]/(x(x-1))$은 normal domain이기는 커녕 integral domain조차 아니다.

한편 affine-local property를 보일 때, $X$의 모든 affine open subset에 대해서 이 성질을 보이는 것은 다소 수고스러운 일이 될 수 있다. 다음 보조정리는 이를 덜어준다.

보조정리 10 Scheme $X$가 주어졌다 하고, $X$의 affine open subscheme들의 성질 $P$가 다음의 두 조건

1. 만일 $\Spec A\hookrightarrow X$가 성질 $P$를 갖는다면, 임의의 $f\in A$에 대하여 $\Spec A_f\hookrightarrow X$ 또한 $P$를 갖는다.
2. 만일 $A=(f_1,\ldots, f_n)$이고 $\Spec A_{f_i}\hookrightarrow X$가 모두 $P$를 갖는다면, $\Spec A\hookrightarrow X$ 또한 $P$를 갖는다.

을 만족한다 하자. 만일 $X=\bigcup\Spec A_i$이고 각각의 $\Spec A_i$들이 성질 $P$를 만족한다면, $X$의 임의의 affine open subset 또한 성질 $P$를 만족한다.

이에 대한 증명보다는 이 보조정리를 활용하는 것이 더 중요하므로, 증명은 생략하기로 한다.

정의 11 Scheme $X$가 locally noetherian인 것은 $X$의 적당한 open affine cover $\{\Spec A_i\}$가 존재하여 각각의 $A_i$가 모두 noetherian인 것이다. 만일 $X$가 추가적으로 quasi-compact이기도 하다면 $X$를 noetherian이라 부른다.

이 정의가 보조정리 10의 두 조건을 만족하는 것은 [가환대수학] §국소화, ⁋명제 7에 의해 자명하다. 이 성질을 locally noetherian이라 부르는 것은 다음 명제에 의한 것이다.

명제 12 Scheme $X$가 locally noetherian인 것과 임의의 affine open subset $U=\Spec A$에 대하여 항상 $A$가 noetherian이 되는 것이 동치이다.

증명

한쪽 방향은 자명하다. 따라서 $X$가 locally noetherian이라 하고, 임의의 affine open subset $U=\Spec A$를 택하자. 우선 다음 주장을 보인다.

주장 1. Locally noetherian scheme $X$는 noetherian ring들의 spectrum으로 이루어진 basis를 갖는다.
증명. 우선 $X$가 locally noetherian이므로, $X$를 noetherian ring들의 spectrum $\Spec B_i$들로 덮을 수 있다. 한편, $B_i$들의 localization $(B_i)_f$들은 모두 noetherian이고, $D(f)\cong \Spec(B_i)_f$들이 $\Spec B_i$의 basis를 이룬다. 이제 임의의 열린집합 $U\subseteq X$에 대해 $U_i=U\cap\Spec B_i$라 하면 $U_i$는 $\Spec B_i$의 열린집합이고, 따라서 $\Spec(B_i)_f$들의 합집합으로 나타날 수 있다. 이로부터 임의의 열린집합 $U\subseteq X$가 noetherian ring들의 spectrum들의 합집합으로 쓰일 수 있음을 안다.

주장 1에 의해, 임의의 affine open set $U=\Spec A$는 noetherian ring들의 spectrum으로 덮일 수 있다. 이제 다음 주장을 보이자.

주장 2. 만일 affine scheme $U=\Spec A$가 noetherian ring들의 spectrum으로 덮일 수 있다면, 유한 개의 $f_1,\ldots, f_r\in A$가 존재하여 $U$를 $\Spec A_{f_1},\ldots, \Spec A_{f_r}$로 덮을 수 있다.
증명. 우선 가정을 통해, $U$의 open affine subset $V=\Spec B$을 $B$가 noetherian이도록 잡자. 그럼 적당한 $f\in A$에 대하여 $D(f)\subseteq V$이도록 할 수 있다. 한편, $f$의 $B$에서의 image를 $\bar{f}$라 하면 $A_f\cong B_{\bar{f}}$가 성립한다. 이로부터 $A_f$가 noetherian임을 안다. 이러한 방식으로 $U$를 noetherian ring들 $A_f$들의 spectrum $\Spec A_f$들로 덮을 수 있다. 그런데

\[X=\bigcup \Spec(A_f)\iff A=\sum A_f\iff 1\in\sum A_f\]

이고, 가장 우측의 조건은 유한 개의 $A_{f_1},\ldots, A_{f_r}$들과, 이들의 원소 $x_1,\ldots, x_r$가 존재하여 $x_1+\cdots+x_r=1$이라는 뜻이므로 이러한 $\Spec A_f$들은 유한 개만이 필요하다.

따라서 우리가 보이고자 하는 것은 다음의 대수적인 주장이다.

주장 3. Ring $A$의 원소들 $f_1,\ldots, f_r$이 다음 조건을 만족한다 하자.

1. $(f_1,\ldots, f_r)=A$이다.
2. $A_{f_i}$들은 모두 noetherian ring들이다.

그럼, $A$도 noetherian이다.
증명. $A$의 임의의 ideal $\mathfrak{a}$와 localization map $\varphi_i:A \rightarrow A_{f_i}$에 대하여, $\mathfrak{a}=\bigcap\varphi_i^{-1}(\varphi_i(\mathfrak{a})\cdot A_{f_i})$이 성립한다. 따라서, 임의의 ascending chain $\mathfrak{a}_1\subseteq \mathfrak{a}_2\subseteq\cdots$에 대하여

\[\varphi_i(\mathfrak{a}_1)A_{f_i}\subseteq\varphi_i(\mathfrak{a}_2)A_{f_i}\subseteq\cdots\]

이 언젠가 반드시 멈춰야 한다는 사실을 이용하면 원하는 결과를 얻는다.