값매김환

우선 다음을 정의해야 한다.

정의 1 임의의 scheme $X$이 주어졌다 하자.

1. $X$의 열린집합 $U$에 대하여, scheme $(U, \mathcal{O}_X\vert_U)$를 $X$의 open subscheme이라 부른다. $f:X \rightarrow Y$이 $X$와 $Y$의 open subscheme 사이의 isomorphism을 유도하면 $f$를 open immersion이라 부른다.
2. Scheme morphism $f:Y \rightarrow X$가 closed immersion이라는 것은 $\lvert Y\rvert$가 $f$에 의하여 $\lvert X\rvert$의 닫힌집합으로의 homeomorphism을 정의하고, $f^\sharp: \mathcal{O}_X \rightarrow f_\ast \mathcal{O}_Y$가 surjective인 것이다.
   만일 두 closed immersion $f:Y \rightarrow X$와 $f’: Y’ \rightarrow X$에 대하여, isomorphism $i:Y’ \rightarrow Y$가 존재하여 $f’=f\circ i$이도록 할 수 있다면 $f$와 $f’$를 equivalent한 closed immersion들이라 생각하고, 이 때 equivalence class를 closed subscheme으로 정의한다. 이와 같은 closed subscheme이 주어졌을 때, $f^\sharp$의 kernel $\mathcal{I}_Y$를 ideal sheaf라 부른다.

정의 2 Scheme morphism $f:X \rightarrow Y$에 대하여, diagonal morphism_대각사상을 $\Delta: X \rightarrow X \times_Y X$으로 정의한다.

만일 $\Delta$가 closed immersion이라면 $f$를 separated라 부르고, $X$가 $Y$에 대해 seperated라 부른다. 만일 $X$가 $\Spec \mathbb{Z}$에 대해 separated이면, $X$를 간단히 separated scheme이라 부른다.

대수기하학에서는 separatedness가 Hausdorff를 대체하는 성질이라 생각하는데, 이는 다음 명제 때문이다.

명제 3 $f:X \rightarrow Y$가 separated인 것과, diagonal morphism $\Delta: X \rightarrow X\times_YX$에 의한 $X$의 image가 닫힌집합인 것이 동치이다.

증명

정의에 의하여 $f$가 separated라면 $\Delta(X)$가 닫혀있음은 자명하다. 따라서 $\Delta(X)$가 closed임을 가정하고, $\Delta$가 closed immersion임을 보여야 한다. $\Delta(X)$가 $X\times_YX$의 닫힌집합이 되는 것은 자명하므로, $\mathcal{O}_{X\times_YX} \rightarrow \Delta_\ast \mathcal{O}_X$가 surjective임을 보이면 충분하다. 한편 sheaf morphism의 surjectivity는 stalk 위에서 체크할 수 있다. 임의의 $p\in X$를 택하자. 그럼 우선 $p$의 open affine subset $U$를 택할 수 있으며, 필요하다면 $U$를 제한하여 $f(U)$가 $Y$의 어떠한 open affine subset $V$에 속하도록 할 수 있다. 그럼 $U\times_VU$는 $\Delta(p)$의 open neighborhood이며, 이 위에서 $\Delta: U \rightarrow U\times_VU$는 다음의 보조정리 4에 의하여 closed immersion이 되고, 증명이 완료된다.

보조정리 4 Affine scheme 사이의 임의의 morphism $f:X \rightarrow Y$는 항상 separated이다.

증명

$X=\Spec A, Y=\Spec B$라 하면 $\Delta$가 ring homomorphism

\[A\otimes_BA \rightarrow A;\quad a\otimes a'\mapsto aa'\]

으로부터 유도되며, 이것이 surjective이므로 자명하다.

Separated가 아닌 scheme의 예시는 §스킴, ⁋예시 6에서 만든 line with double origin이 있다. 역시, 위상수학에서 이 공간은 Hausdorff가 아닌 공간의 예시였다.

다음 정리는 separated morphism에 대한 쓸만한 기준을 준다.

정리 5 Noetherian scheme $X$와 scheme morphism $f:X \rightarrow Y$에 대하여, $f$가 separated인 것은 임의의 valuation ring $R$과 그 quotient field $K$에 대하여, 임의의 scheme morphism $\Spec R \rightarrow Y$, $\Spec K \rightarrow X$와 다음 commutative diagram

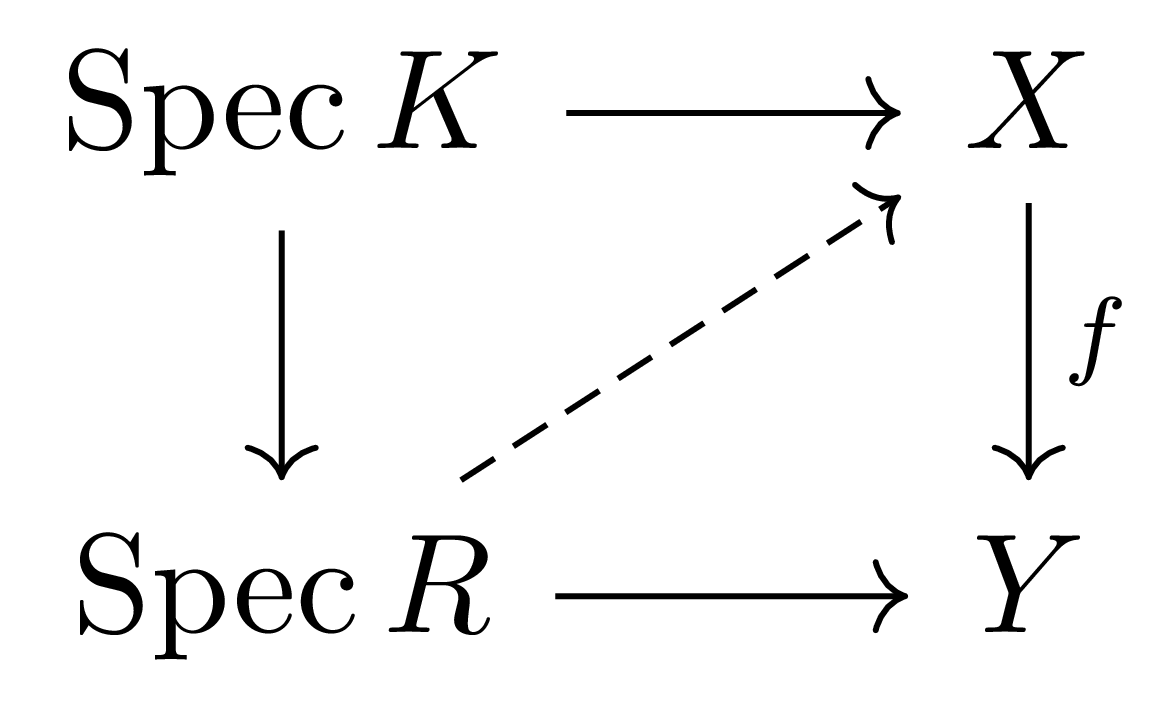
의 바깥쪽 square가 주어질 때마다, 많아야 하나의 $\Spec R \rightarrow X$가 존재하여 전체 diagram이 commute하는 것이 동치이다.