K

Grad. student in mathematics

범주론 카테고리의 글은 기본적으로 [집합론] 카테고리의 글만 읽으면 이해할 수 있도록 되어있고, 이번 글에서 다루는 모노이드 카테고리 또한 그런 방식으로 글을 쓸 수도 있지만 특별히 이번 글의 첫 번째 부분은 이해를 돕기 위해 [대수적 구조] 카테고리의 글을 가져오게 되었다.

이번 글과 다음 글에서는 monoidal category와 그 안에서 정의된 monoidal object에 대해 살펴본다. 대략적으로 이야기해서 monoid object란 대수적으로 정의했던 monoid와 비슷한 성질을 갖는 어떤 category의 대상인데, 이 때 monoid와 비슷한 성질을 갖는다는 이야기를 하기 위해서는 이 category가 monoidal category여야 한다. 따라서 우리는 우선 대수적으로 monoid가 어떤 것이었는지를 가볍게 복습한 후, 어떻게 하면 이 이야기를 category의 언어로 바꾸어 쓸 수 있는지를 생각해본다.

모노이드

우리는 associative unital magma를 monoid모노이드라 부르기로 하였다. ([대수적 구조] §반군, 모노이드, 군, ⁋정의 3) 이를 풀어 써보자면 $M$이 monoid라는 것은 다음과 같은 뜻이다.

$M$ 위에서 정의된 이항연산 $\mu:M\times M \rightarrow M$과, $M$의 원소 $e\in M$이 존재하여,

  1. (Associativity) 임의의 $a,b,c\in M$에 대하여 $\mu(\mu(a,b),c)=\mu(a,\mu(b, c))$가 성립한다.
  2. (Unit element) $e\in M$은 임의의 $a\in M$에 대하여, $a\cdot e=e\cdot a=a$를 만족한다.

그런데, 이들 조건들은 각각 commutative diagram으로 나타낼 수 있다. 우선 associativity의 경우, 다음 diagram이 commute한다는 것과 같은 뜻이다.

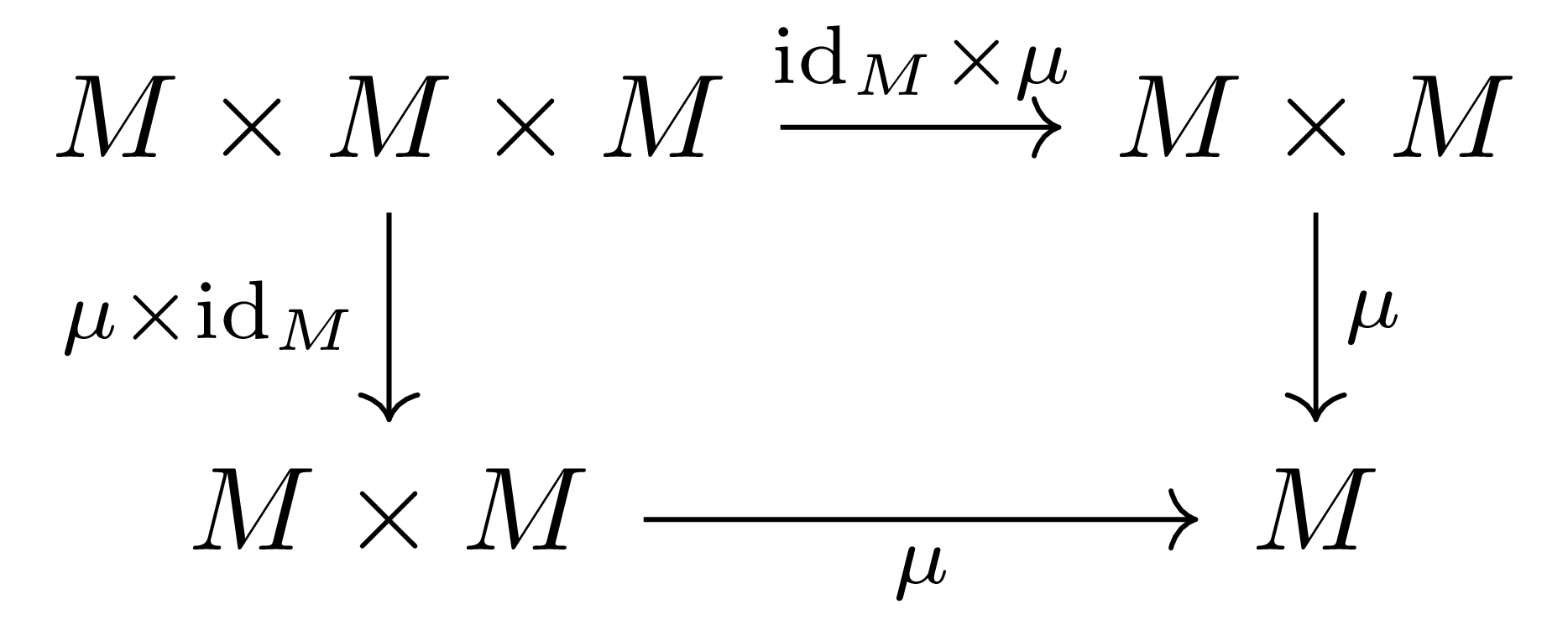
Associativity

이는 당연한 것이, 왼쪽 위에 있는 집합의 임의의 원소 $(a,b,c)$를 뽑아오면, $\urcorner$ 방향으로 진행할 경우에는

\[\mu(\mu(a,b),c)=\mu(a\cdot b,c)=(a\cdot b)\cdot c\]

를 얻고, 비슷하게 $\llcorner$ 방향으로 진행할 경우에는

\[\mu(a,\mu(b,c))=\mu(a,b\cdot c)=a\cdot(b\cdot c)\]

를 얻는데, 이 diagram이 commute한다는 것이 정확히 이 두 $M$의 원소가 서로 같다는 뜻이기 때문이다.

비슷하게 항등원 $e$의 경우는, 집합 $I=\{e\}$와 inclusion $i:I\hookrightarrow M$을 이용하면 다음 diagram

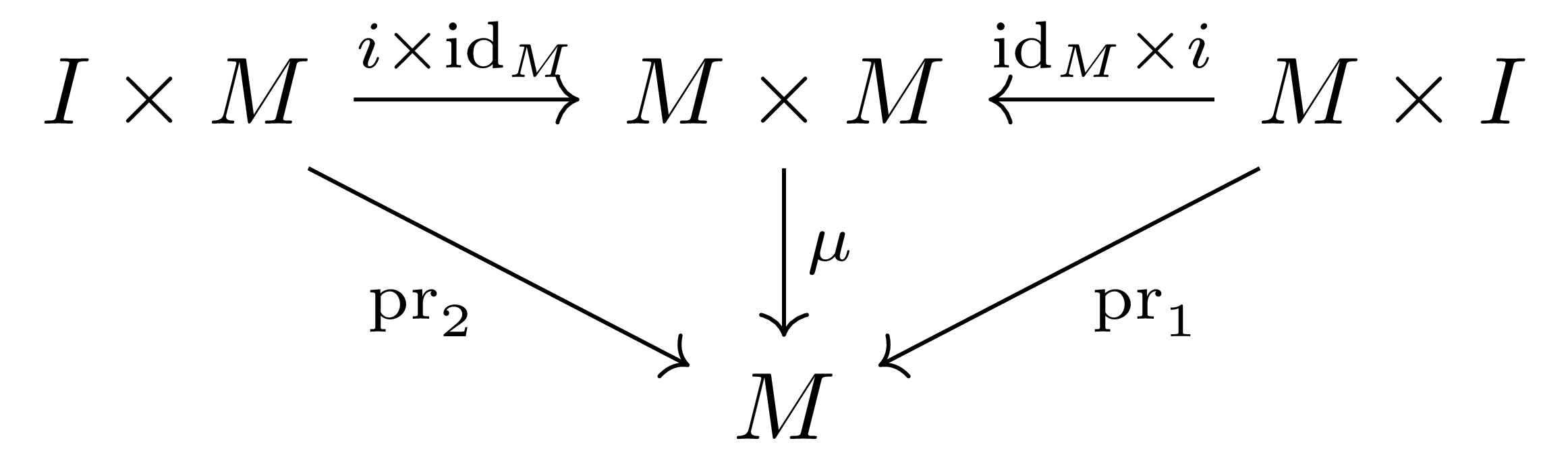
Unit_element

이 commute한다는 것으로 쓸 수 있다.

범주론에서는 어떤 대상에서 원소를 뽑아오거나 하는 것이 불가능하다. 따라서 맨 처음 살펴본 monoid의 정의는 범주론을 이용하여 설명하기 부적절하다. 그러나 위와 같이 모든 것을 diagram으로 나타내게 되면, 이를 적당히 범주론의 언어로 올려줄 수 있다. 이를 위해서는 우선 우리가 자연스럽게 사용했던 $M\times M$이 무엇인지부터 정의해야 할 것이다.1

모노이드 카테고리

간단히 말해서, monoidal category란 대상들 사이의 monoid operation, 즉 associative하고 항등원을 가지는 연산이 주어지는 category이다. 얘컨대 우리가 맨 앞에서 monoid를 정의할 때 사용했던 $\times$는 $\Set$을 monoidal category로 만든다는 것을 곧 살펴볼 것이다.

정의를 하기에 앞서, monoid를 정의하는 두 diagram에서 $M\times(M\times M)$과 $(M\times M)\times M$은 서로 다른 집합이고, $M$, $I\times M$, $M\times I$도 서로 다른 집합이라는 것을 기억하자. 이들은 분명 서로 다른 집합들이며, 다만 이들 사이에 자연스러운 isomorphism들이 존재할 뿐이다.

정의 5 (Monoidal category) Monoidal category모노이드 범주는 데이터 $(\mathcal{A},\otimes, I)$로 이루어진다. 여기서 $\mathcal{A}$는 category이고, $I\in\obj(\mathcal{A})$이며, $\otimes:\mathcal{A}\times \mathcal{A}\rightarrow \mathcal{A}$가 bifunctor이다. 이들은 다음 조건을 만족한다.

  1. $\mathcal{A}\times \mathcal{A}\times \mathcal{A}$에서 $\mathcal{A}$로의 두 functor $-\otimes(-\otimes-)$와 $(-\otimes-)\otimes-$사이의 natural isomorphism

    \[\alpha_{A,B,C}:A\otimes(B\otimes C)\rightarrow (A\otimes B)\otimes C\]

    이 존재한다. 이를 associator라 부른다.

  2. $\mathcal{A}$에서 $\mathcal{A}$로의 세 functor $I\otimes-$, $-\otimes I$, $\id_\mathcal{A}$들 간의 natural isomorphism들

    \[\lambda_A:I\otimes A\rightarrow A,\qquad \rho_A:A\otimes I\rightarrow A\]

    이 존재한다. $\lambda$와 $\rho$를 각각 left unitor와 right unitor라 부른다.

  3. (Coherence condition) 다음 두 diagram이 모두 commute한다.

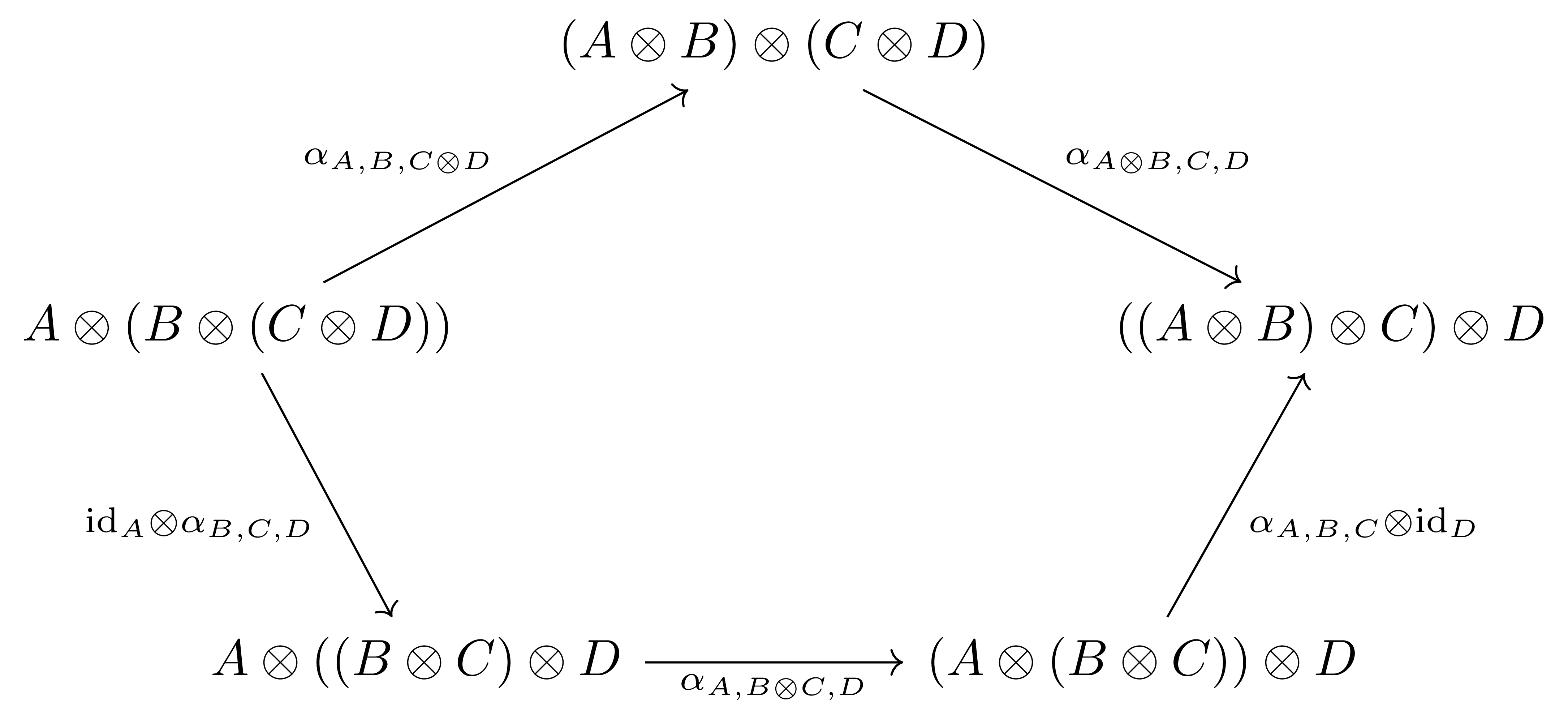
  • (Associator) Pentagon_identity
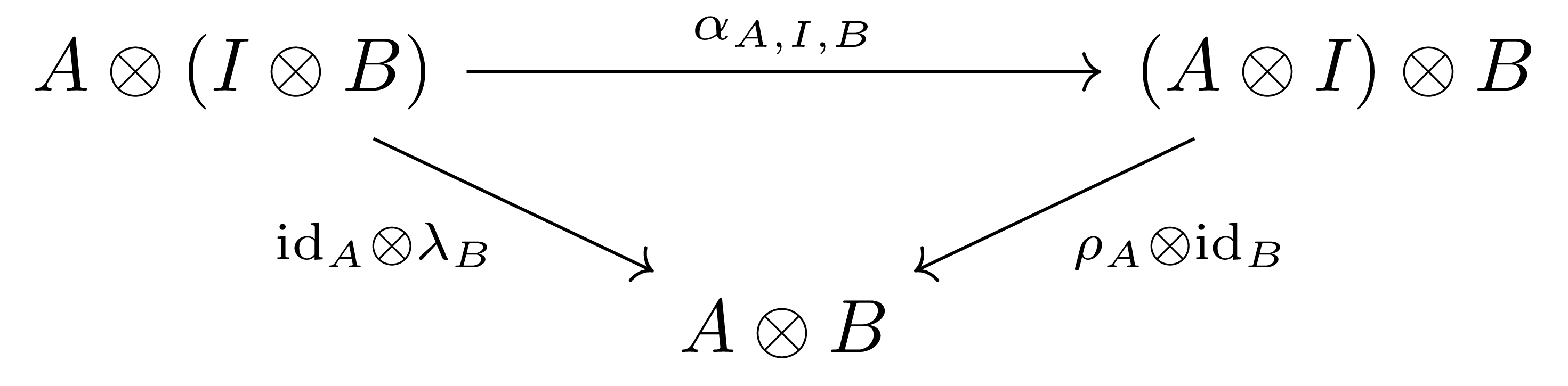
  • (Unitor) unitor_diagram

만일 monoidal category $(\mathcal{A},\otimes,I)$에 추가적으로 $\otimes$의 symmetric 조건이 추가되면 이를 symmetric monoidal category대칭 모노이드 범주라 부른다. 이는 natural isomorphism (symmetor) $\gamma_{AB}:A\otimes B \rightarrow B\otimes A$과, 다음의 추가적인 coherence condition들

  • (Associativity coherence) associativity_coherence
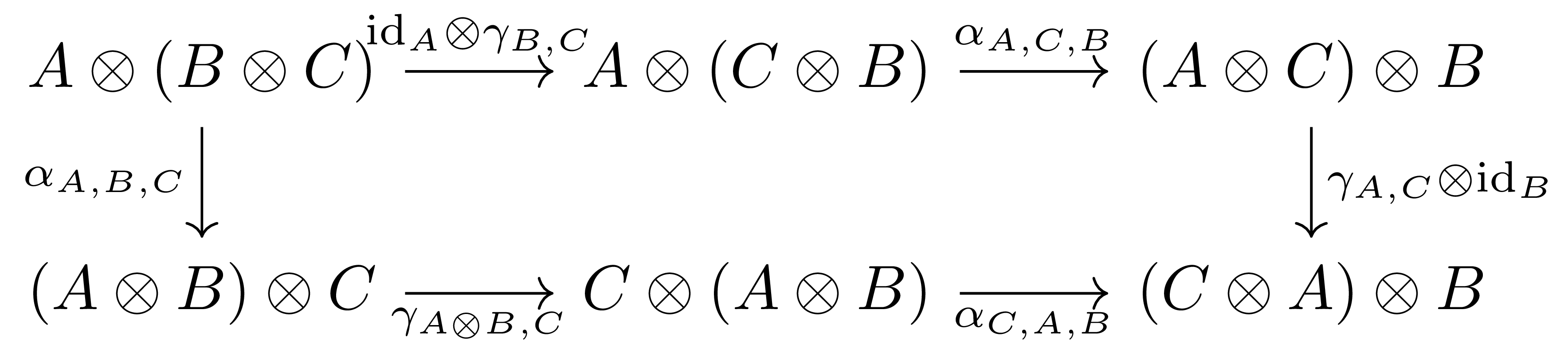
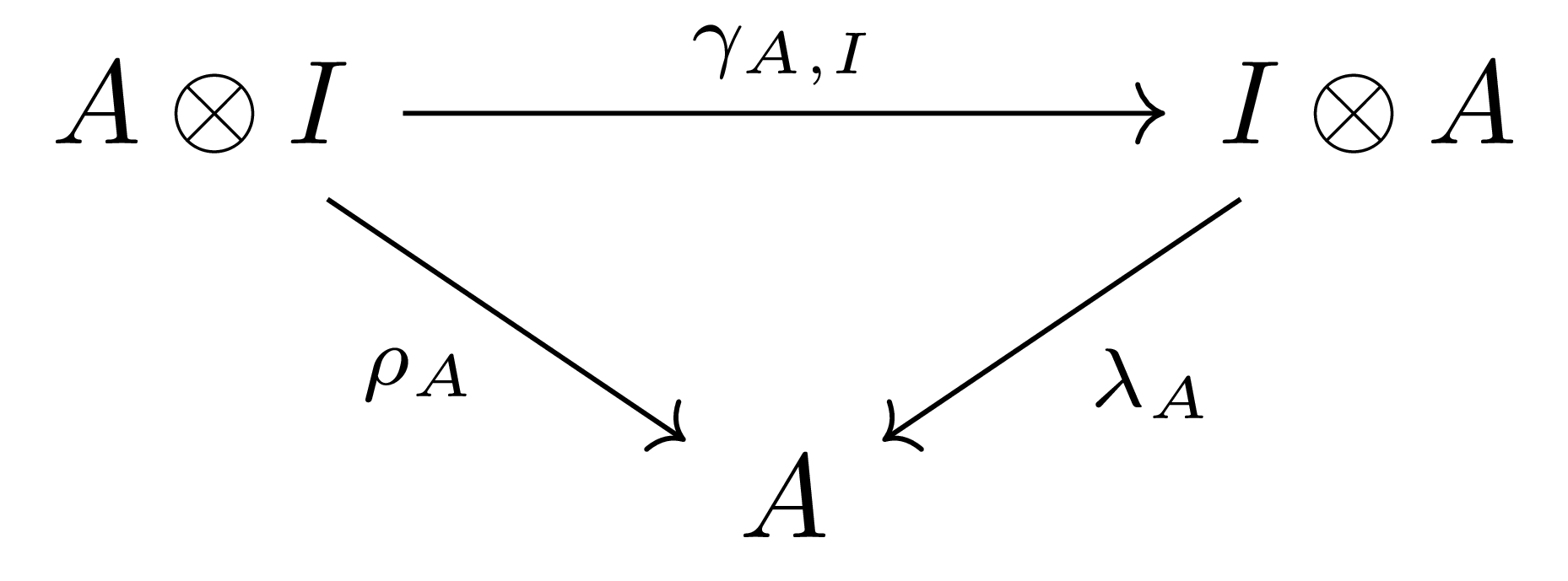
  • (Unit coherence) symmetor
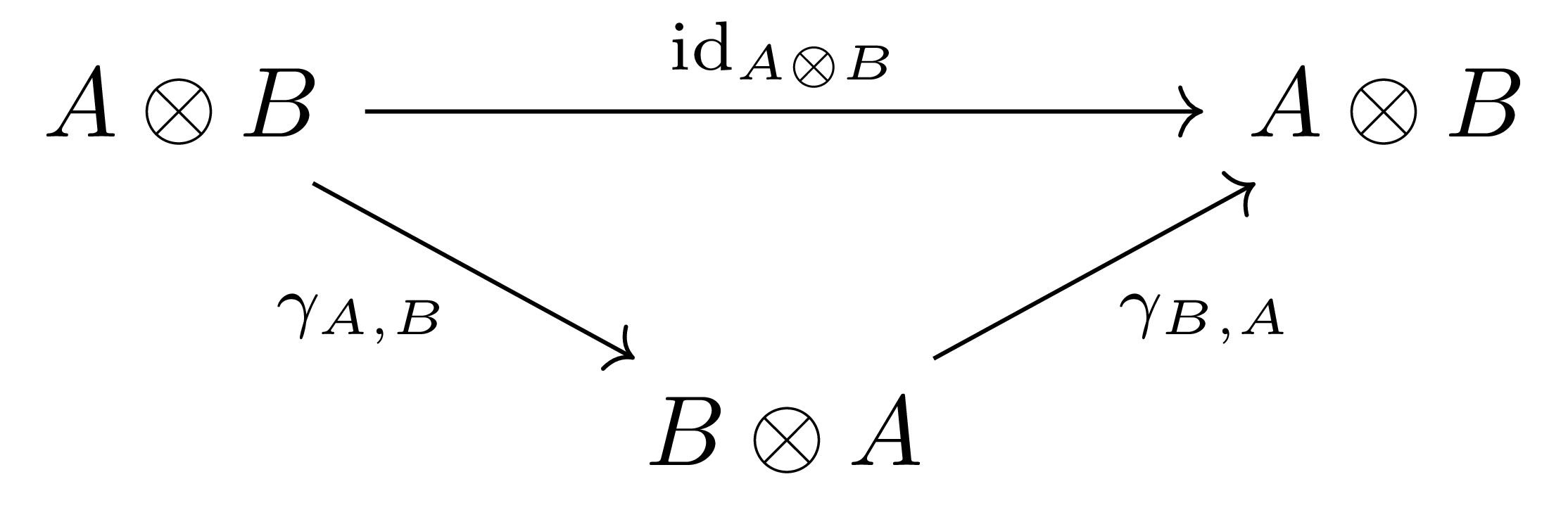
  • (Inverse law) inverse

으로 나타난다.

만일 symmetric monoidal category에서, $\gamma_{A,B}:A\otimes B\rightarrow B\otimes A$와 $\gamma_{B,A}:B\otimes A \rightarrow A\otimes B$가 서로의 inverse가 아니라면, 이를 braided monoidal category매듭 모노이드 범주라 부른다.

Associator와 unitor들의 coherence condition은 Mac Lane의 coherence theorem을 증명할 때 사용된다. 대략적으로 말해서, 이는 $n$개의 대상들의 곱 $A_1\otimes\cdots\otimes A_n$이 주어졌을 때, 이를 어떤 것부터 계산하거나 (symmetric monoidal category의 경우) 배열된 순서를 바꾸어 계산하더라도 그 결과들이 naturally isomorphic하며, 이것이 associator, unitor, (symmetric monoidal category인 경우) symmetor들의 합성으로 유일하게 나타난다는 것이다.

어쨌든 coherence theorem 덕분에 우리는 monoidal product가 계산순서 혹은 이들이 나열된 순서에 의존하지 않는다는 것을 알고 있으므로 이제 이들 natural isomorphism은 상대적으로 덜 신경써도 된다.

예시 6 다음은 모두 monoidal category의 예시들이다.

  • $\Set$에 일반적인 product (§극한, ⁋예시 6)를 장착하고, $I$는 아무 singleton으로 가져오면 $\Set$은 symmetric monoidal category가 된다.
  • $\Grp$에 일반적인 product를 장착하고, $I$는 trivial group $\{e\}$으로 가져오면 $\Grp$이 symmetric monoidal category가 된다.
  • $\Top$에 product 구조를 product topology로 주고, $I$는 아무 singleton으로 가져오면 $\Top$은 symmetric monoidal category가 된다.
  • 임의의 commutative ring $R$에 대하여, $R$-module들의 카테고리 $\lMod{R}$은 tensor product $\otimes$에 대해 symmetric monoidal category이다.
  • 특히 $R=k$인 경우 위의 예시는 $\Vect_k$가 symmetric monoidal category임을 보여주고, $R=\mathbb{Z}$인 경우 우리는 $\Ab$이 symmetric monoidal category임을 알 수 있다.

예시 6의 앞의 두 예시는 일반화가 가능하다. 우선 다음을 정의하자.

정의 7 Category $\mathcal{A}$의 대상들의 유한한 family가 항상 categorical product를 갖는다면, 이 category를 cartesian category라 부른다.

그럼 앞선 예시에서, $\Set$과 $\Grp$은 cartesian category가 된다. 마찬가지로 $\Top$이나 $\Man^\infty$ 등도 모두 cartesian category이다.

명제 8 임의의 cartesian category는 monoidal category의 구조를 갖는다.

이 명제의 증명을 위해서는 많은 말을 덧붙여야 하긴 하지만, 본질적으로 이는 $(A\times B)\times C\cong A\times(B\times C)$와 $I\times M\cong M\cong M\times I$들이 어떻게 나왔는지를 떠올린 후, 계산들을 반복하면 된다. 이와 같이, monoidal product가 product로 주어진 monoidal category를 cartesian monoidal category라 부른다.

Cartesian monoidal category가 일반적인 monoidal category와 다른 점 중 하나는 몇 가지 자연스러운 morphism들이 잘 정의가 된다는 것이다. 가령 일반적인 monoidal category에서는 잘 정의되지 않는 diagonal morphism $\Delta_X:X \rightarrow X\times X$이나 augmentation morphism $\epsilon_X:X \rightarrow I$가 잘 정의된다. $\epsilon_X$는 $I$가 terminal object이므로 자연스럽게 정의되고, $\Delta_X$는 다음 diagram을 통해 얻어진다.

diagonal_morphism

이는 다음 글에서 group object를 다룰 때 사용된다.

참고문헌

[nLab] nLab. Monoidal category. (Link)
[Rie] Emily Riehl. Category Theory in Context. Dover Publications, 2016.

  1. 앞에서 두 category 사이의 곱을 정의한 적은 있어도, 한 category 안에서 두 대상들의 곱은 정의한 적이 없다. ↩

댓글남기기