K

Grad. student in mathematics

함자의 정의와 기본 성질

수학에서 다루는 모든 대상들과 이들 사이의 morphism들의 모임을 category로 보겠다는 범주론의 철학을 받아들이기로 한다면, 자연스럽게 우리가 정의한 수학적인 대상, 즉 category들을 대상으로 갖는 category를 생각할 수도 있다. 이를 위해서는 우선 category들 사이의 morphism이 무엇인지부터 정의해야 한다.

정의 1 두 category \(\mathcal{A},\mathcal{B}\) 사이의 functor함자 \(F:\mathcal{A}\rightarrow\mathcal{B}\)는 다음과 같은 정보로 구성된다.

  • 각각의 \(A\in\obj(\mathcal{A})\)마다 대응되는 object \(F(A)\in\obj(\mathcal{B})\),
  • 각각의 \(f\in\Hom_\mathcal{A}(A_1,A_2)\)마다 대응되는 morphism \(F(f)\in\Hom_\mathcal{B}(F(A_1),F(A_2))\)

이들은 다음 조건들을 만족한다.

  • 두 morphism의 합성을 \(F\)로 보낸 것은 각각의 morphism을 \(F\)로 보낸 후 합성한 것과 같다. 즉 \(F(g\circ f)=F(g)\circ F(f)\)가 성립한다.
  • 임의의 object \(A\in\obj(\mathcal{A})\)에 대하여, \(F(\id_A)=\id_{F(A)}\)가 성립한다.

어렵지 않게 functor들의 합성이 functor인 것을 보일 수 있다.

보조정리 2 임의의 category들 \(\mathcal{A},\mathcal{B},\mathcal{C}\)와 두 functor \(F:\mathcal{A}\rightarrow \mathcal{B}, G:\mathcal{B}\rightarrow \mathcal{C}\)에 대하여, \(G\circ F:\mathcal{A} \rightarrow \mathcal{C}\)를

  • 임의의 \(A\in \mathcal{A}\)에 대하여, \((G\circ F)(A)=G(F(A))\),
  • 임의의 \(f\in\Hom_\mathcal{A}(A_1,A_2)\)에 대하여, \((G\circ F)(f)=G(F(f))\)

으로 정의하면 \(G\circ F\)는 functor가 된다.

증명

Functor가 만족해야 하는 두 조건만 보이면 충분하며, 이는

\[(G\circ F)(g\circ f)=G(F(g\circ f))=G(F(g)\circ F(f))=G(F(g))\circ G(F(f))=(G\circ F)(g)\circ(G\circ F)(f)\]

그리고

\[(G\circ F)(\id_A)=G(F(\id_A))=G(\id_{F(A)})=\id_{G(F(A))}=\id_{(G\circ F)(A)}\]

으로부터 자명하다.

함자의 예시들

우리는 임의의 preordered set을 category로 볼 수 있다는 것을 살펴보았다. (§카테고리, ⁋예시 3) 다음 예시는 여기에 새로운 관점을 부여한다. 고정된 category \(\mathcal{I}\)와 임의의 category \(\mathcal{A}\)에 대하여, functor \(F:\mathcal{I}\rightarrow \mathcal{A}\)를 \(\mathcal{I}\)-shaped diagram in \(\mathcal{A}\)라 부르자.

예시 3 집합 \(I_1=\{a,b,c\}\)와, 다음 관계 \(a\leq b\leq c\)로 주어진 preorder relation을 생각하자. 그럼 \((I_1,\leq)\)로부터 만들어지는 category \(\mathcal{I}_1\)은 다음 그림

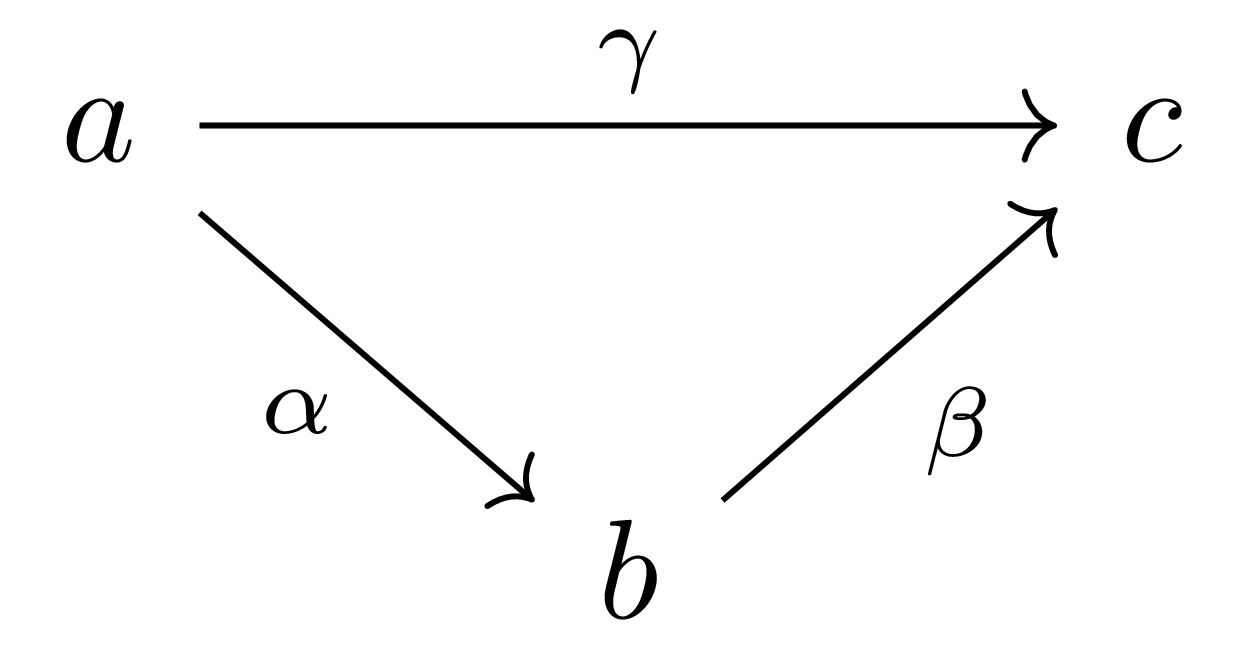
commuting_triangle

으로 표현할 수 있다. 이제 functor \(F:\mathcal{I}_1 \rightarrow \mathcal{A}\)는 다음 조건

\[F(\beta)\circ F(\alpha)=F(\beta\circ\alpha)=F(\gamma)\]

을 만족한다. 즉, \(\mathcal{A}\)의 대상 \(F(a),F(b),F(c)\)와 이들 사이의 morphism \(F(\alpha):F(a) \rightarrow F(b)\), \(F(\beta):F(b) \rightarrow F(c)\), \(F(\gamma): F(a) \rightarrow F(c)\)에 대하여 다음 그림

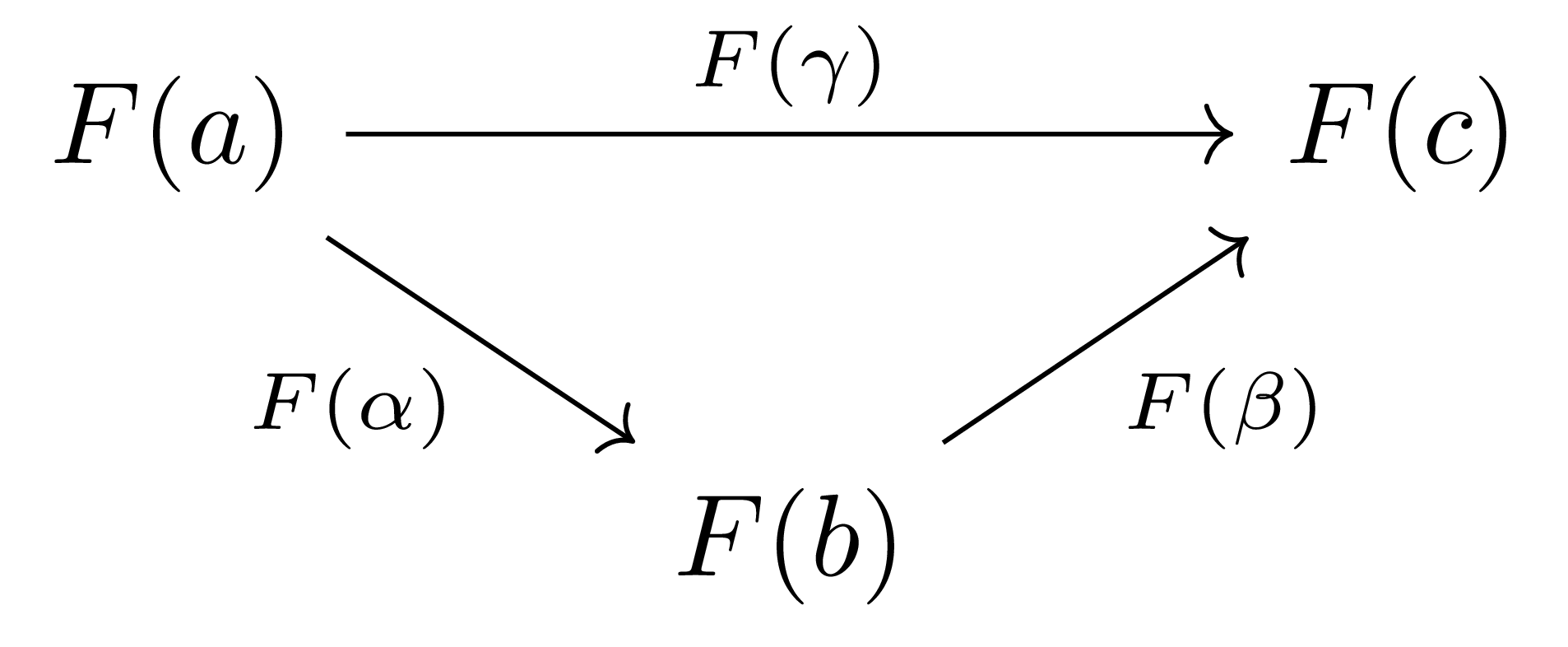
commuting_triangle_F

이 (이전까지 생각해왔던 의미로서) commutative triangle이 된다. 거꾸로 이러한 조건을 만족하는 데이터는 모두 이와 같은 식으로 \(\mathcal{I}_1\)으로부터의 functor로 생각할 수 있다.

비슷하게, 집합 \(I_2=\{a,b,c,d\}\) 위에 다음 관계들 \(a\leq b,c\), 그리고 \(b,c\leq d\)로 preorder relation을 주면 functor \(\mathcal{I}_2 \rightarrow \mathcal{A}\)는 commutative square가 된다.

이와 같은 직관을 살리기 위해 \(\mathcal{I}\rightarrow \mathcal{A}\)를 diagram으로 생각할 때는 \(\mathcal{I}\)의 대상들을 \(i,j,k,...\)으로 표기한다.

예시 4 Locally small category \(\mathcal{A}\)와 대상 \(A\in\obj(\mathcal{A})\)를 고정하자. 그럼 임의의 \(B\in\obj(\mathcal{A})\)가 주어질 때마다 집합 \(\Hom_\mathcal{A}(A,B)\)를 대응시키는 것은 \(\mathcal{A}\)에서 \(\Set\)으로의 functor이다. 이를 확인하기 위해서는 임의의 \(f:B \rightarrow B'\)가 주어질 때마다 morphism \(\Hom_\mathcal{A}(A,B)\rightarrow\Hom_\mathcal{A}(A,B')\)를 대응시켜주면 되는데, 이를

\[\Hom_\mathcal{A}(A, f):\Hom_\mathcal{A}(A,B)\rightarrow\Hom_\mathcal{A}(A,B');\qquad \phi\mapsto f\circ\phi\]

으로 정의하자.

covariant hom

그럼 이러한 데이터로 주어지는 대응 \(\Hom_\mathcal{A}(A,-)\)이 functor가 된다는 것을 확인할 수 있다.

반변함자

예시 4와 같은 방식으로 functor \(\Hom_\mathcal{A}(-,A)\)를 정의해볼 수 있다. 그러나 이 경우, 다음의 diagram

contravariant Hom

에서 확인할 수 있듯 \(\Hom_\mathcal{A}(f,A)\)는 \(\Hom_\mathcal{A}(B',A)\)에서 \(\Hom_\mathcal{A}(B,A)\)로의 morphism이 되어버린다.

정의 5 두 category \(\mathcal{A},\mathcal{B}\) 사이의 contravariant functor반변함자는 다음과 같은 정보로 구성된다.

  • 각각의 \(A\in\obj(\mathcal{A})\)마다 대응되는 object \(F(A)\in\obj(\mathcal{B})\),
  • 각각의 \(f\in\Hom_\mathcal{A}(A_1,A_2)\)마다 대응되는 morphism \(F(f)\in\Hom_\mathcal{B}(F(A_2),F(A_1))\)

이들은 다음 조건들을 만족한다.

  • \(\mathcal{A}\)의 두 morphism의 합성을 \(F\)로 보낸 것은 각각의 morphism을 \(F\)로 보낸 후 방향을 바꾸어 합성한 것과 같다. 즉 \(F(g\circ f)=F(f)\circ F(g)\)가 성립한다.
  • 임의의 object \(A\in\obj(\mathcal{A})\)에 대하여, \(F(\id_A)=\id_{F(A)}\)가 성립한다.

이와 같은 정의 때문에, 정의 1의 functor를 더 정확하게는 covariant functor공변함자라 부르기도 한다. 그러나 functor라 하면 보통 covariant functor만을 뜻하는데, 이는 다음 정의에 의해 모든 contravariant functor를 어떤 종류의 covariant functor로 생각할 수 있기 때문이다.

정의 6 Category \(\mathcal{A}\)가 주어졌다 하자. 그럼 \(\mathcal{A}\)의 opposite category반대 카테고리 \(\mathcal{A}^\op\)는 다음의 데이터로 이루어진다.

  • \(\obj(\mathcal{A}^\op)=\obj(\mathcal{A})\)이다.
  • 임의의 \(A,B\in \obj(\mathcal{A}^\op)=\obj(\mathcal{A})\)에 대하여, \(\Hom_{\mathcal{A}^\op}(A,B)=\Hom_{\mathcal{A}}(B,A)\)가 성립한다.
  • 임의의 \(A\in\obj(\mathcal{A})\)에 대하여, \(\mathcal{A}^\op\)에서의 identity \(\id_A\)는 \(\mathcal{A}\)에서의 identity와 동일한 것으로 주어진다.

  • 임의의 \(f\in\Hom_{\mathcal{A}^\op}(A,B),g\in\Hom_{\mathcal{A}^\op}(B,C)\)에 대하여, 이들의 합성 \(g\circ^\op f\)는 \(f,g\)를 \(\mathcal{A}\)의 morphism들로 본 후, 이를 \(\mathcal{A}\)에서 합성한 것으로 정의된다.
    즉, \(f\in \Hom_\mathcal{A}(B,A),g\in\Hom_\mathcal{A}(C,B)\)에 대하여, \(f\)와 \(g\)의 \(\mathcal{A}^\op\)에서의 합성 \(g\circ^\op f\)는

    \[g\circ^\op f= f\circ g\in\Hom_{\mathcal{A}}(C,A)=\Hom_{\mathcal{A}^\op}(A,C)\]

    으로 정의된다.

이 정의 하에서, 정의 5를 다시 쓰자면 \(\mathcal{A}\)에서 \(\mathcal{B}\)로의 contravariant functor란 단순히 (covariant) functor \(\mathcal{A}^\op \rightarrow \mathcal{B}\)에 불과하다.

Bifunctor

다음 정의는 우리가 이미 알고있는 것들로만 이루어져 있긴 하지만, 그래도 이름을 붙여주면 종종 요긴하게 사용할 수 있다.

정의 7 세 category \(\mathcal{A}, \mathcal{B}, \mathcal{C}\)에 대하여, functor \(\mathcal{A}\times \mathcal{B}\rightarrow \mathcal{C}\)를 bifunctor라 부른다.

예시 8 임의의 (locally small) category \(\mathcal{A}\)에 대하여, \(\Hom_\mathcal{A}(-,-): \mathcal{A}^\op\times \mathcal{A}\rightarrow \Set\)는 bifunctor이다.

이를 확인하기 위해서는 functoriality만 확인하면 충분하다. 정의에 의하여, \(\mathcal{A}^\op\times \mathcal{A}\)의 morphism은

\[(g,h):(A_1,A_2) \rightarrow (A_1',A_2');\qquad g\in \Hom_{\mathcal{A}^\op}(A_1,A_1'),\quad h\in \Hom_\mathcal{A}(A_2,A_2')\]

의 꼴이며, bifunctor \(\Hom_\mathcal{A}(-,-)\)를 통해 이 morphism은 다음 morphism

\[\Hom_\mathcal{A}(g,h):\Hom_\mathcal{A}(A_1,A_2) \rightarrow \Hom_\mathcal{A}(A_1',A_2');\qquad f\mapsto h\circ f\circ g\]

으로 보내진다. 여기에서 \(\mathcal{A}'\)에서의 morphism \(g\)를 \(\mathcal{A}\)에서의 morphism \(A_1'\rightarrow A_1\)으로 보았다.

카테고리 \(\Cat\)

이를 통해 category들의 category를 정의할 수 있다. 다만 이전에 언급했던 러셀의 역설과 관련된 문제를 피하기 위해 우리는 보편적으로 모든 category들의 category 대신, 모든 small category들의 category 혹은 모든 locally small category들의 category를 생각한다.

정의 9 Category \(\Cat\)는 다음의 데이터로 이루어진다.

  • \(\Cat\)의 대상들은 small category들이다.
  • 임의의 \(\mathcal{A},\mathcal{B}\in\obj(\Cat)\)에 대하여, \(\Hom_\Cat(\mathcal{A},\mathcal{B})\)는 \(\mathcal{A}\)에서 \(\mathcal{B}\)로의 functor들의 모임이다.

비슷하게, category \(\CAT\)는 다음의 데이터로 이루어진다.

  • \(\CAT\)의 대상들은 locally small category들이다.
  • 임의의 \(\mathcal{A},\mathcal{B}\in\obj(\CAT)\)에 대하여, \(\Hom_\CAT(\mathcal{A},\mathcal{B})\)는 \(\mathcal{A}\)에서 \(\mathcal{B}\)로의 functor들의 모임이다.

이들 데이터가 실제로 category가 된다는 것을 확인할 수 있다.

정의 10 Locally small category들 \(\mathcal{A}, \mathcal{B}\)에 대하여, functor \(F:\mathcal{A}\rightarrow \mathcal{B}\)가 faithful충실하다는 것은 임의의 \(A_1,A_2\in\obj(\mathcal{A})\)에 대하여, 대응

\[\Hom_\mathcal{A}(A_1,A_2)\rightarrow\Hom_{\mathcal{B}}(F(A_1),F(A_2));\qquad f\mapsto F(f)\]

이 injective인 것이다. 만일 이 대응이 surjective라면 \(F\)가 full충만이라 한다.

참고문헌

[Rie] Emily Riehl. Category Theory in Context. Dover Publications, 2016.

댓글남기기