K

Grad. student in mathematics

모노이드 대상

이제 우리는 monoid object를 정의할 수 있다.

정의 1 Monoidal category $(\mathcal{A},\otimes, I)$에서의 monoid object모노이드 대상이란 다음의 데이터

  • 대상 $M$,
  • multiplication $\mu:M\otimes M \rightarrow M$,

  • unit $\eta:I \rightarrow M$ 으로 주어진다. 이들은 다음 조건을 만족한다.

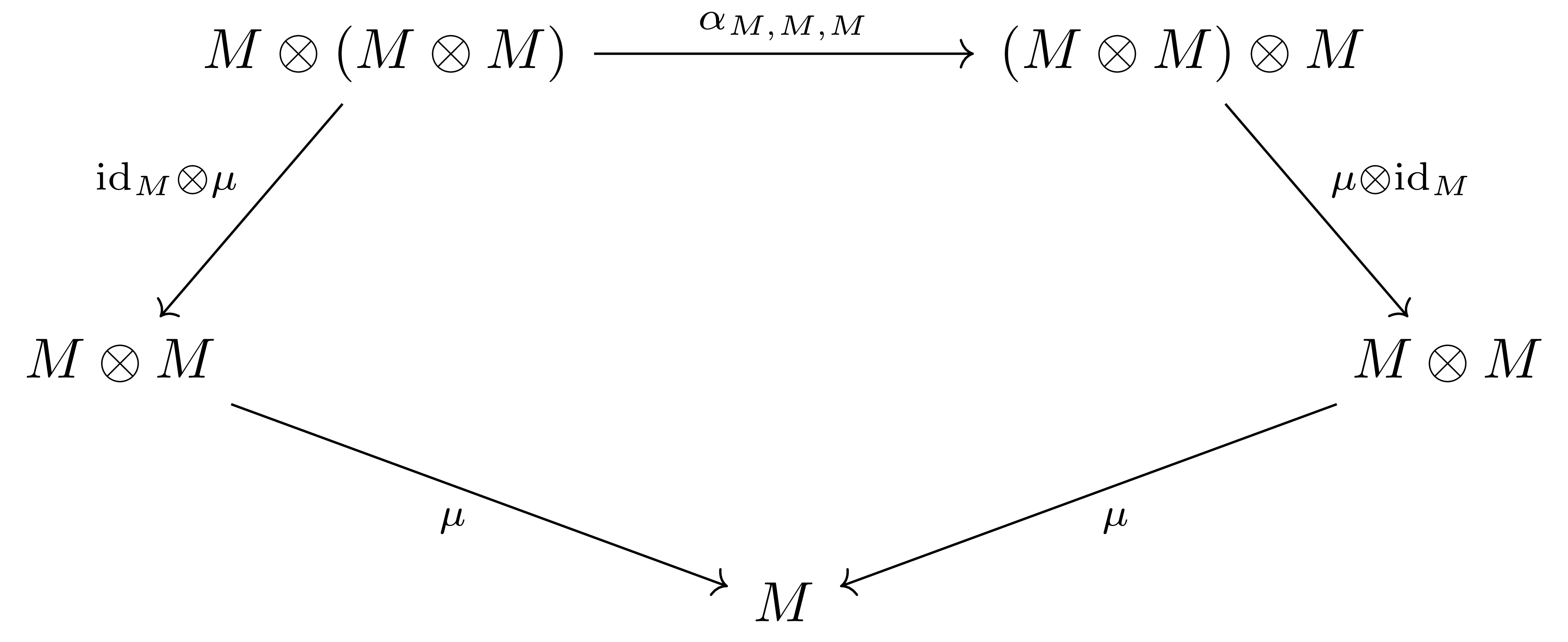
  • (Associativity)1 associativity
  • (Unit) unit

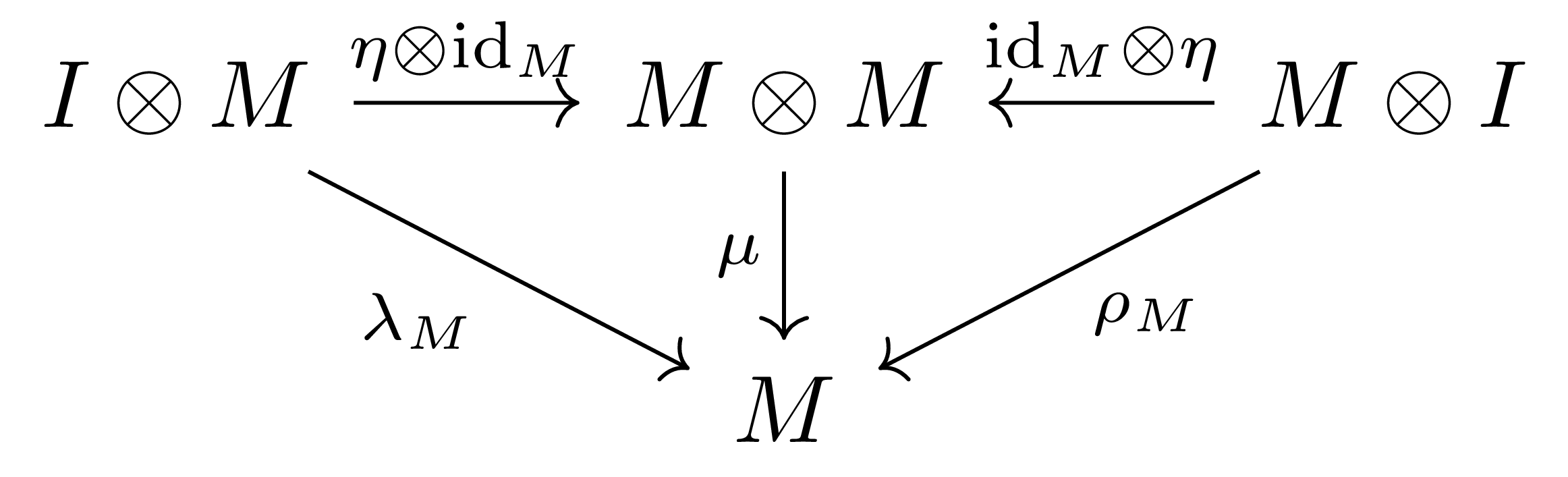
임의의 monoidal category $(\mathcal{A},\otimes, I)$는 항상 monoid object $I$를 갖는다. 또, $M$이 symmetric monoidal category의 monoid object라면 $M\otimes M$ 또한 monoid object가 된다는 것을 쉽게 확인할 수 있다.

예시 2 다음은 모두 monoid object들의 예시이다.

  • Cartesian monoidal category $\Set$에서 monoid object는 일반적인 의미에서의 monoid이다.
  • $\Top$에서의 monoidal object는 topological monoid이다.
  • 임의의 commutative ring $R$에 대하여, $(\lMod{R},\otimes_R, R)$의 monoid object는 associative unital $R$-algebra이다.
  • 임의의 commutative ring $R$에 대하여, $(\Ch(R),\otimes_R, R)$의 monoid object는 differential graded $R$-algebra이다. 여기서 unit $R$은 degree $0$에 $R$이 있고, 나머지 degree는 모두 $0$인 chain complex이다.

위의 예시를 범주론의 관점이 아니라, 우리가 기존에 알고 있던 대수적인 언어로 설명할 필요가 있다.

우선 첫 번째 예시의 경우, $\Set$에서의 monoid object $(M,\mu,\eta)$를 일반적인 monoid로 생각할 수 있다는 것은 다음과 같은 뜻이다. Monoid $M$의 underlying set은 $M$이며, multiplication $\mu:M\times M \rightarrow M$을 통해 $M$ 위에서의 연산이 정의된다. 한편 $\Set$에서의 terminal object는 singleton이므로, unit $\eta$의 $M$에서의 image는 $M$의 어떤 하나의 원소가 될 것인데, 이를 monoid의 unit으로 생각할 수 있다. 비슷하게 두 번째 예시도 설명할 수 있다.

세 번째 예시를 살펴보기 위해서는 $\lMod{R}$의 symmetric monoidal category의 구조를 먼저 살펴보는 것이 좋다. Cartesian monoidal category들과는 다르게, $\lMod{R}$에서의 monoidal product는 categorical product가 아닌 tensor product로 주어져있고, 따라서 unit object 또한 terminal object가 아니라 $R$이다. Unitor들의 경우, $R$-module $M$이 하나 주어질 때마다 $\lambda_M$은

\[\lambda_M: R\otimes M \rightarrow M;\quad r\otimes m\mapsto rm\]

으로 결정되는 isomorphism이고, 비슷하게 $\rho_M$은 $m\otimes r\mapsto rm$을 통해 유일하게 결정되는 $R$-linear map이다.

$\lMod{R}$의 임의의 대상은 이미 덧셈구조가 존재한다. $\lMod{R}$에서의 monoid object $(M,\mu,\eta)$는 $M$이 가지고 있는 덧셈구조에 더하여 이 덧셈구조와 호환되는 곱셈구조가 생기는 것으로 이해할 수 있으며, 이러한 방식으로 $M$이 $R$-algebra가 된다. 이 때, 덧셈구조와 곱셈구조가 호환된다는 것, 즉 분배법칙과 같은 것들이 성립한다는 사실은 $M\otimes M \rightarrow M$의 임의의 원소와, $M\times M$에서 $M$으로의 $R$-bilinear map 사이의 일대일대응이 존재한다는 사실로부터 얻어진다.

$M$에 곱셈구조를 주기 위해 마지막으로 남는 것은 이 곱셈에 대한 항등원인데, 이 정보는 $\eta:R \rightarrow M$로부터 정해줄 수 있다. $R$ 위에 정의된 left $R$-module 구조를 생각해보면, $\eta$가 담고 있는 정보는 정확히 $\eta(1)$과 동등하고, 이 원소 $\eta(1)\in M$이 새로 정의한 곱셈에 대한 항등원 역할을 한다.

\[\mu(\eta(1)\otimes m)=\mu((\eta\otimes\id_M)(1\otimes m))=\lambda_M(1\otimes m)=m\]

그리고 비슷하게 right unitor를 사용하면 $\mu(m\otimes\eta(1))=m$도 보일 수 있기 때문이다.

임의의 monoidal category $\mathcal{A}$에 대하여, 이 위에 정의된 monoid object들 사이의 morphism도 정의할 수 있고, 따라서 monoid object들의 category 또한 생각할 수 있다. 그러나 이 방향으로 monoid category를 정의하거나 하지는 않을 것이다.

군 대상

앞선 정의와 비슷하게, 우리는 group object를 정의할 수 있다. 이를 위해서는 monoid object를 정의할 때 그러했듯 group의 각 성질들을 diagram으로 나타낼 필요가 있다. Group $(G, \mu, e,(-)^{-1})$은 정확히 다음의 조건을 만족한다.

  • $(G,\mu,e)$는 monoid이다.

  • $(-)^{-1}:G \rightarrow G$는 모든 $g\in G$에 대하여, 다음 식

    \[\mu(g^{-1},g)=\mu(g,g^{-1})=e\]

    을 만족한다.

그런데 이를 monoidal category의 언어로 옮겨쓰려면 문제가 있다. 둘째 조건을 diagram으로 써 보면,

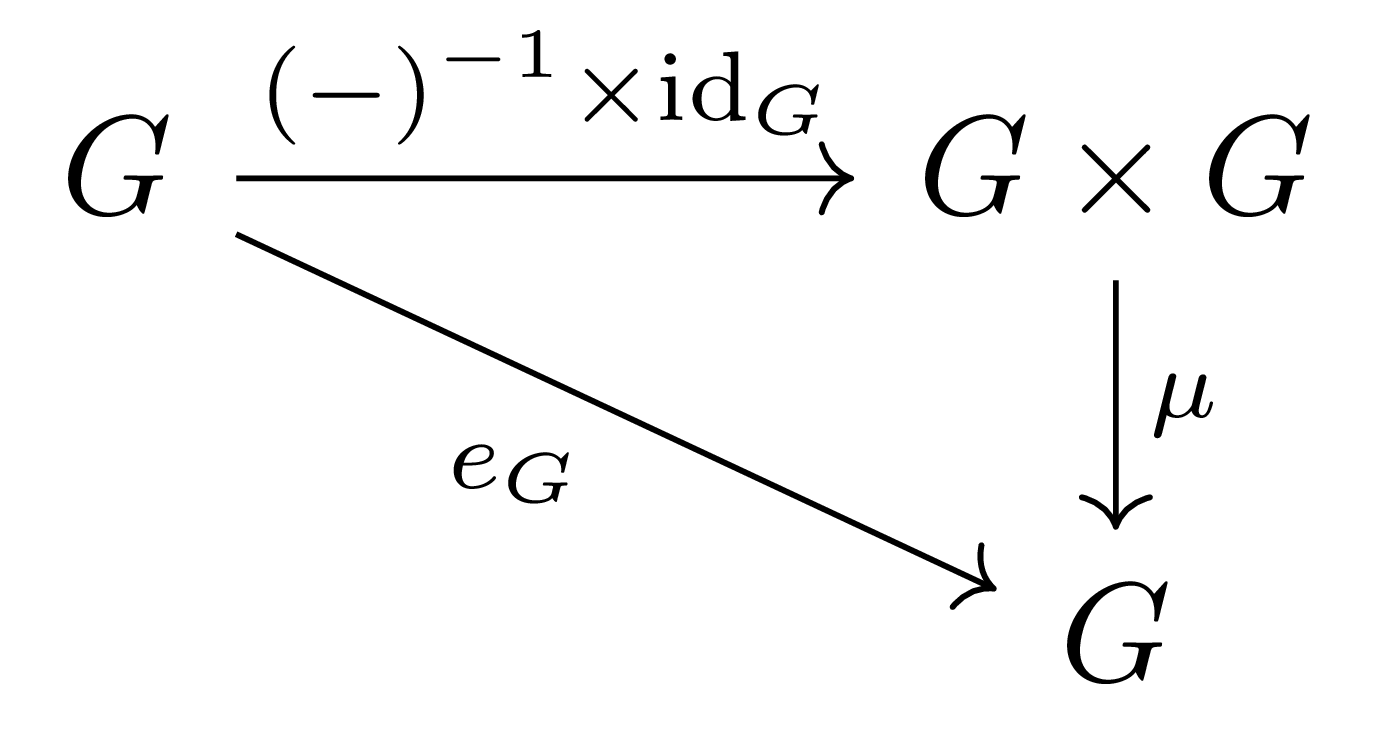
group_axiom

가 되어야 할 것이다. 여기에서 $e_G$는 $G$의 모든 원소를 $G$의 항등원으로 보내는 group homomorphism이고, $(-1)^{-1}\times \id_G$는 두 map $(-)^{-1}:G \rightarrow G$와 $\id_G:G \rightarrow G$의 곱이다. 물론 두 데이터를 전부 추가해서 이를 group object라 할 수도 있겠지만, 그렇게 한다면 예컨대 (monoid object로서의) unit $\eta:I \rightarrow G$와 새로 정의한 morphism $e_G$가 서로 아무런 관련이 없을 것이기 때문에 좋은 해결책이 아니다.

그런데 만일 원래의 category가 monoidal category가 아니라, cartesian monoidal category였다면 이 모든 문제가 깔끔하게 해결된다. 우선 $e_G$의 경우는 다음의 합성

\[G\overset{\epsilon_G}{\longrightarrow}\{e\}\overset{\eta}{\longrightarrow}G\]

으로 주어진다. 여기에서 $\epsilon_G$는 $G$에서 terminal object $\{e\}$로 가는 유일한 morphism이고 $\eta$는 monoid object로서의 $G$의 unit이다. 뿐만 아니라, cartesian monoidal category에서는 monoidal product가 categorical product이므로, 다음 diagram

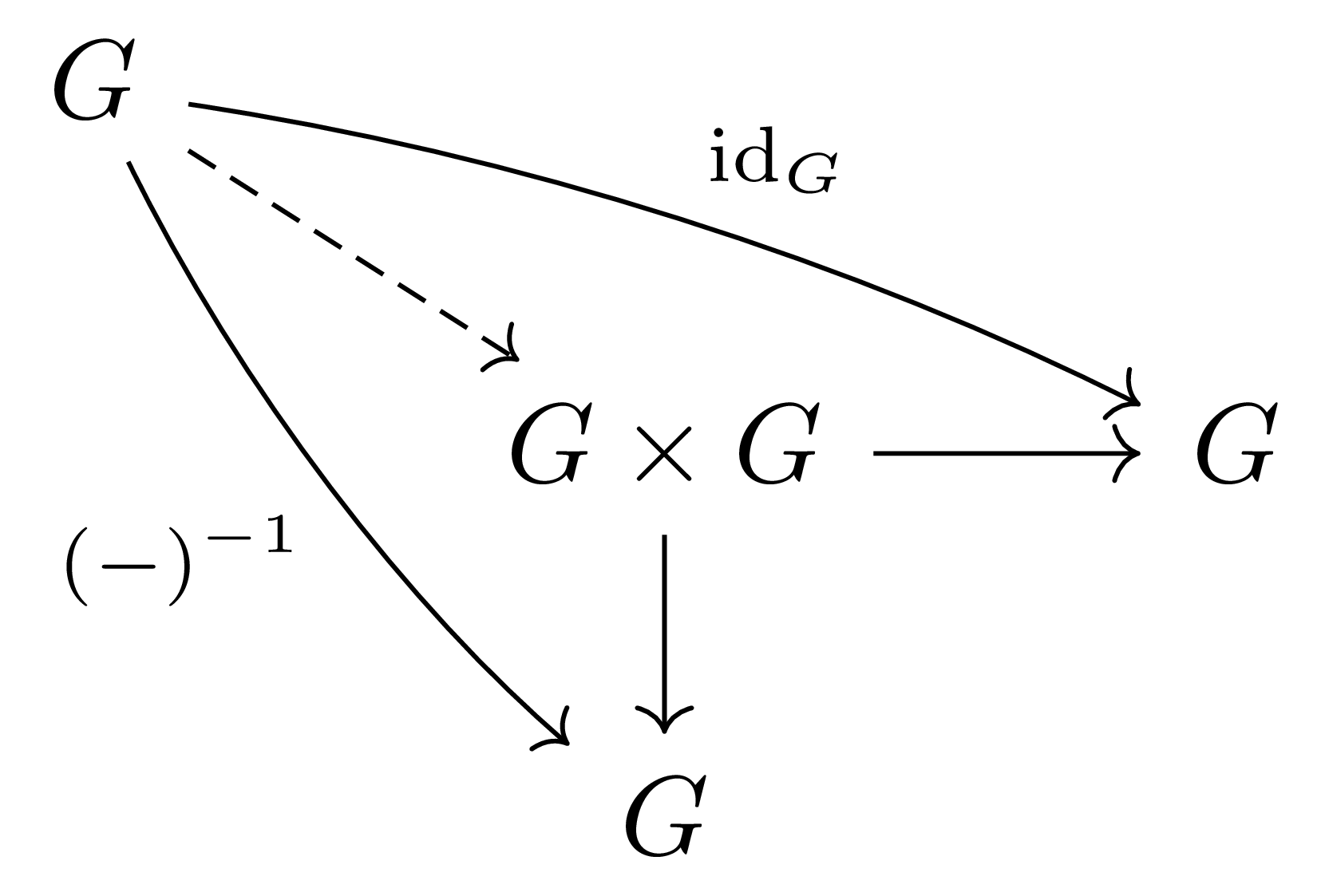
inverse_morphism

을 통해 $(-1)^{-1}\times \id_G$이 잘 정의된다.

정의 3 Cartesian monoidal category $(\mathcal{A},\times, I)$에 대하여, 이 category에서의 group object군 대상은 다음과 같은 데이터

  • 대상 $G$,
  • multiplication $\mu:G\otimes G \rightarrow G$,
  • unit $\eta:I \rightarrow G$,
  • inverse $\iota:G \rightarrow G$

으로 주어진다. $e_G$를 합성 $G\rightarrow I\overset{\eta}{\rightarrow}G$라 하면, 이들은 다음 조건을 만족한다.

  • (Associativity) 다음 diagram 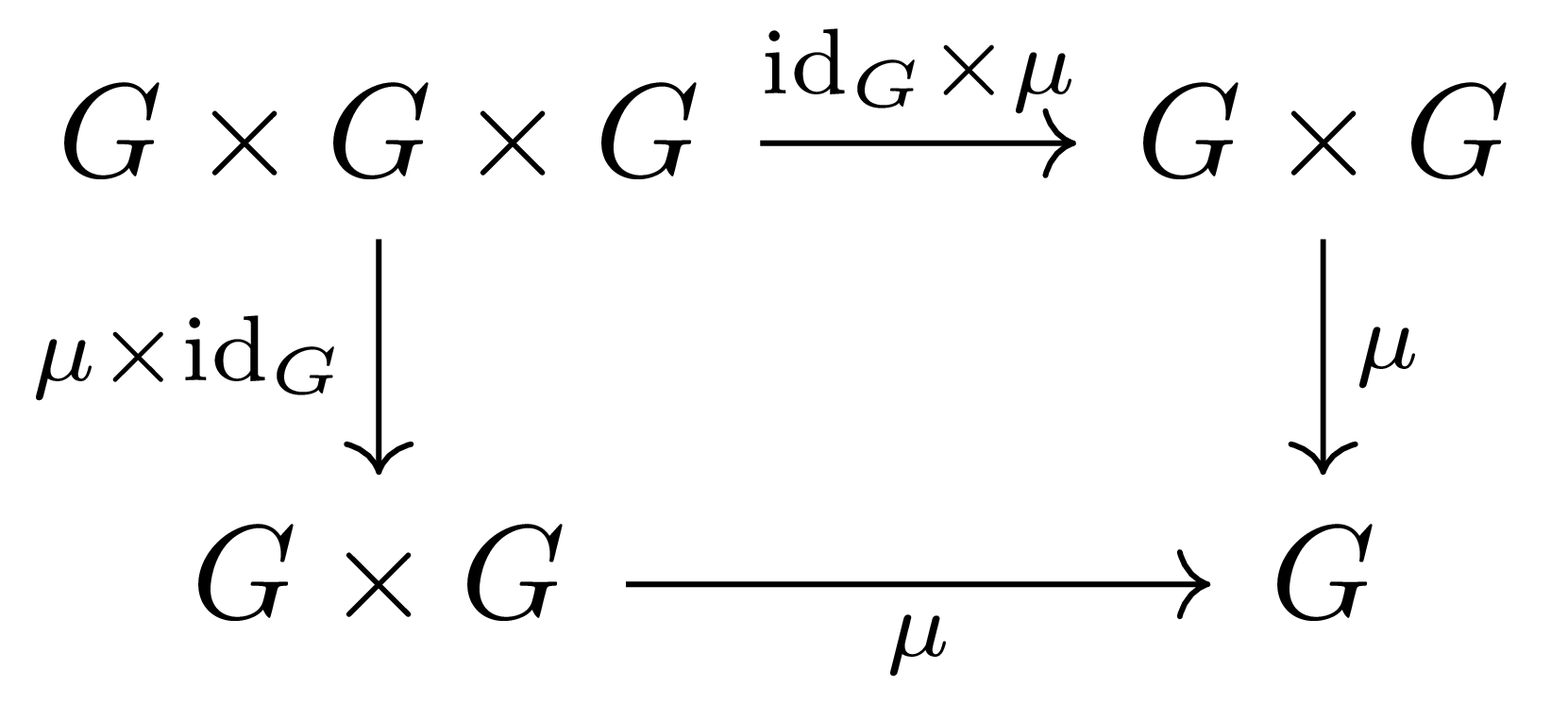associative_group_law 이 commute한다.
  • (Unit element) 다음 diagram identity_element 이 commute한다.
  • (Inverse element) 다음 diagram inverse_element 이 commute한다.

정의 3은 cartesian monoidal category에서부터 시작했기 때문에, categorical product의 universal property를 이용하면 위와 같이 associator와 unitor들을 빼고 diagram을 그릴 수 있었다. 이들을 모두 살려서 적는다면 처음 두 diagram은 정확히 monoid object의 조건이고, 마지막 조건이 새롭게 추가된 것으로 볼 수 있다.

예시 4 다음은 모두 group object이다.

  • $\Set$에서의 group object는 group이다.
  • $\Top$에서의 group object는 topological group이다.
  • $\Man^\infty$에서의 group object는 Lie group이다.
  • $\Var$에서의 group object는 algebraic group이다.
  • $\Sch$에서의 group object는 group scheme이다.
  • $\Grp$에서의 group object는 abelian group이다.

마지막 예시만이 조금 덜 자명해보일 수 있지만, 이는 inverse $\iota$가 group homomorphism이 되어야하기 때문에 이 조건으로부터 commutativity가 나오게 된다는 것을 확인할 수 있다.

Hopf monoid

위의 정의 3을 만들 때 필요했던 것을 살펴보면, 우리가 필요한 것은 정확히 diagonal map $\Delta: G \rightarrow G\otimes G$와 augmentation map $G \rightarrow I$, 그리고 inverse map $I \rightarrow G$이다. 여기에서 필요한 것들을 잘 나눠보면 우선 다음을 정의할 수 있다.

정의 5 Monoidal category $(\mathcal{A},\otimes,I)$가 주어졌다 하자. $\mathcal{A}$의 대상 $M$이 comonoid쌍대모노이드라는 것은 $M$이 $\mathcal{A}^\op$에서 monoid object인 것이다.

이를 풀어 써 보자면, comonoid가 담고 있는 정보는 comultiplication쌍대곱 $\Delta: G \rightarrow G\otimes G$와 counit쌍대단위원 $\epsilon:G \rightarrow I$으로 이루어지며, 이들은 정의 1의 두 조건의 dual 버전을 만족한다.

정의 6 Symmetric monoidal category $(\mathcal{A},\otimes,I)$가 주어졌다 하자. 그럼 $(M,\mu,\eta,\Delta,\epsilon)$이 bimonoid라는 것은 다음과 같은 뜻이다.

  • $(M,\mu,\eta)$이 monoid이다.
  • $(M,\Delta,\epsilon)$이 comonoid이다.
  • Comultiplication과 counit이 모두 monoid morphism이다.

Monoid object $M$이 주어졌을 때, $M\otimes M$에 monoid 구조를 주기 위해서는 symmetor의 역할이 중요하기 때문에, 일반적으로 bimonoid의 개념도 symmetric monoidal category에서만 정의한다. 이제 Hopf monoid를 다음과 같이 정의한다.

정의 7 Symmetric monoidal category $(\mathcal{A},\otimes,I)$에서 $(H,\mu,\eta,\Delta,\epsilon,\iota)$가 Hopf monoid호프 모노이드라는 것은 $(H,\mu,\eta,\Delta,\epsilon)$이 bimonoid이고 $\iota$가 정의 3의 마지막 diagram과 동일한 조건을 만족하는 것이다.

$\iota$에 대한 조건을 명시적으로 쓰기 위해서는 정의 3에서 주어졌던 diagram을 모두 Hopf monoid가 갖고 있는 정보로 옮겨야 하는데, 가령 한쪽 삼각형은 다음의 diagram

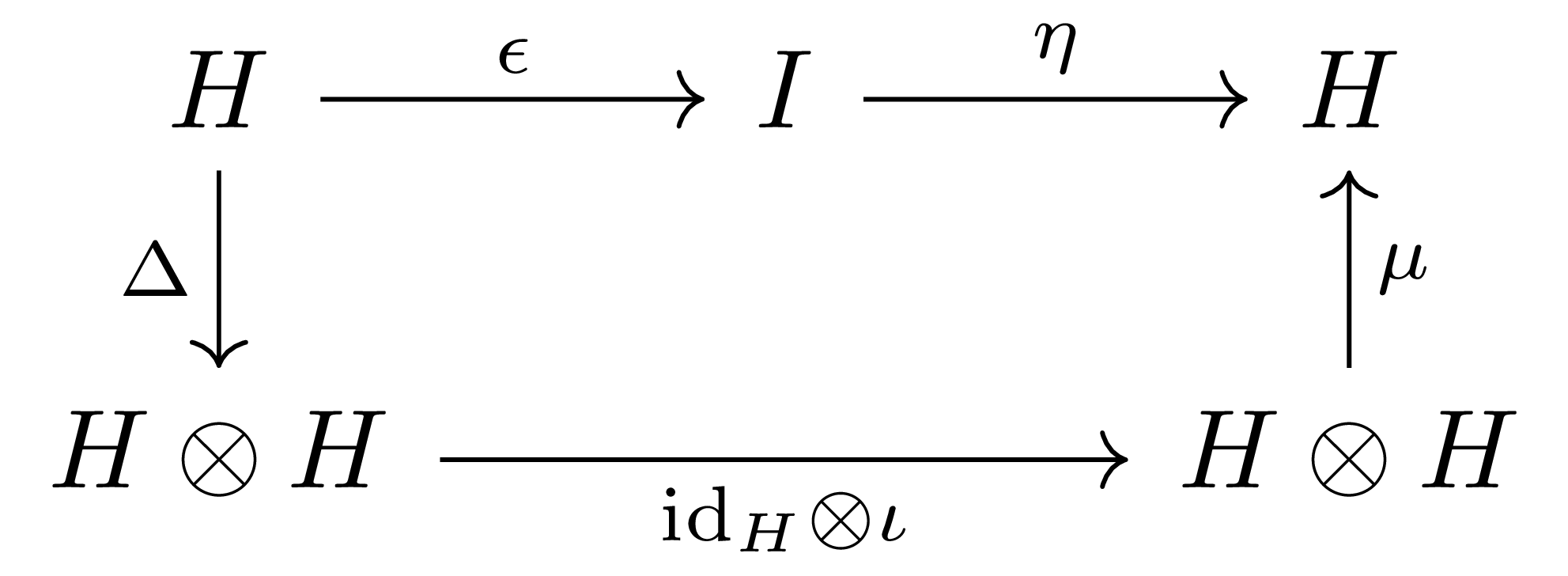
Hopf_inverse

으로 풀어쓸 수 있고, 비슷하게 $\iota\otimes\id_H$을 쓰면 다른 쪽 삼각형을 얻는다.

예시 8 다음은 모두 Hopf monoid의 예시이다.

  • 임의의 cartesian monoidal category에서의 monoid object는 자연스러운 bimonoid 구조를 가지며, 따라서 임의의 cartesian monoidal category에서의 group object는 모두 Hopf monoid이다.
  • $\Vect$에서의 Hopf monoid는 Hopf algebra이다.

참고문헌

[nLab] nLab. Monoidal category. (Link)
[Rie] Emily Riehl. Category Theory in Context. Dover Publications, 2016.

  1. 이전 글에서 motivation을 위해 살펴보았던 monoid의 associativity에 대한 diagram에서는 $(M\times M)\times M$과 $M\times(M\times M)$을 모두 같은 것으로 보아 diagram이 사각형이었지만, 여기에서는 $(M\otimes M)\otimes M$과 $M\otimes(M\otimes M)$이 다른 대상이므로 오각형이 되었다. ↩

댓글남기기