부분공간

부분공간의 정의

대수적인 구조를 다룰 때와 마찬가지로, 집합 $X$ 위에 위상구조를 준 후에는 이 구조가 부분집합 $A\subseteq X$에는 어떠한 방식으로 제한되는지를 살펴보는 것이 자연스럽다. 가장 먼저 드는 생각은 $X$의 열린집합들 가운데, $A$에 포함된 열린집합들만 추려 이들을 위상공간 $A$의 열린집합들로 정의하는 것이다. 그러나 이 시도는 실패할 수밖에 없는데, $A$가 $X$에서 열린집합이 아니라면, 전체집합 $A$부터가 이 모임에 속하지 않기 때문이다.

정의 1 위상공간 $(X,\mathcal{T})$와, $X$의 부분집합 $A$가 주어졌다 하자. 이 때, $\iota:A\hookrightarrow X$에 의해 $A$ 위에 정의되는 initial topology를 $A$ 위에 정의된 부분위상_{subspace topology}이라 부른다.

$X$의 임의의 열린집합 $U$에 대하여, $\iota^{-1}(U)=U\cap A$이고, 임의의 열린집합들의 family $(U_i)_{i\in I}$에 대해

\[\iota^{-1}\left(\bigcup_{i\in I} U_i\right)=\left(\bigcup_{i\in I} U_i\right)\cap A=\bigcup_{i\in I} (U_i\cap A)=\bigcup_{i\in I} \iota^{-1}(U)\]

그리고 열린집합들의 유한한 family $(U_i)_{i\in I}$에 대하여

\[\iota^{-1}\left(\bigcap_{i\in I} U_i\right)=\left(\bigcap_{i\in I} U_i\right)\cap A=\bigcap_{i\in I} (U_i\cap A)=\bigcap_{i\in I} \iota^{-1}(U)\]

이 성립하므로 §Initial topology와 final topology, ⁋명제 2에 의하여 부분위상 $\mathcal{T}_A$는 다음의 식

\[\mathcal{T}_A=\{U\cap A\mid U\in\mathcal{T}\}\]

으로 주어진다는 것을 알 수 있다. [Mun]과 같은 책에서는 아예 이를 부분공간의 정의로 삼기도 한다. 이로부터 만약 $A\subseteq B\subseteq X$라면, $A$를 $X$의 부분공간으로 생각하든, 혹은 부분위상이 주어진 $B\subseteq X$의 부분공간으로 생각하든 동일한 공간이 된다는 것을 알 수 있다.

부분공간을 다룰 때 주의해야 하는 것은 어떤 집합이 $\mathcal{T}_A$에서 열린집합이라 하더라도 $\mathcal{T}$에서는 열린집합이 아닐 수 있다는 것이다.

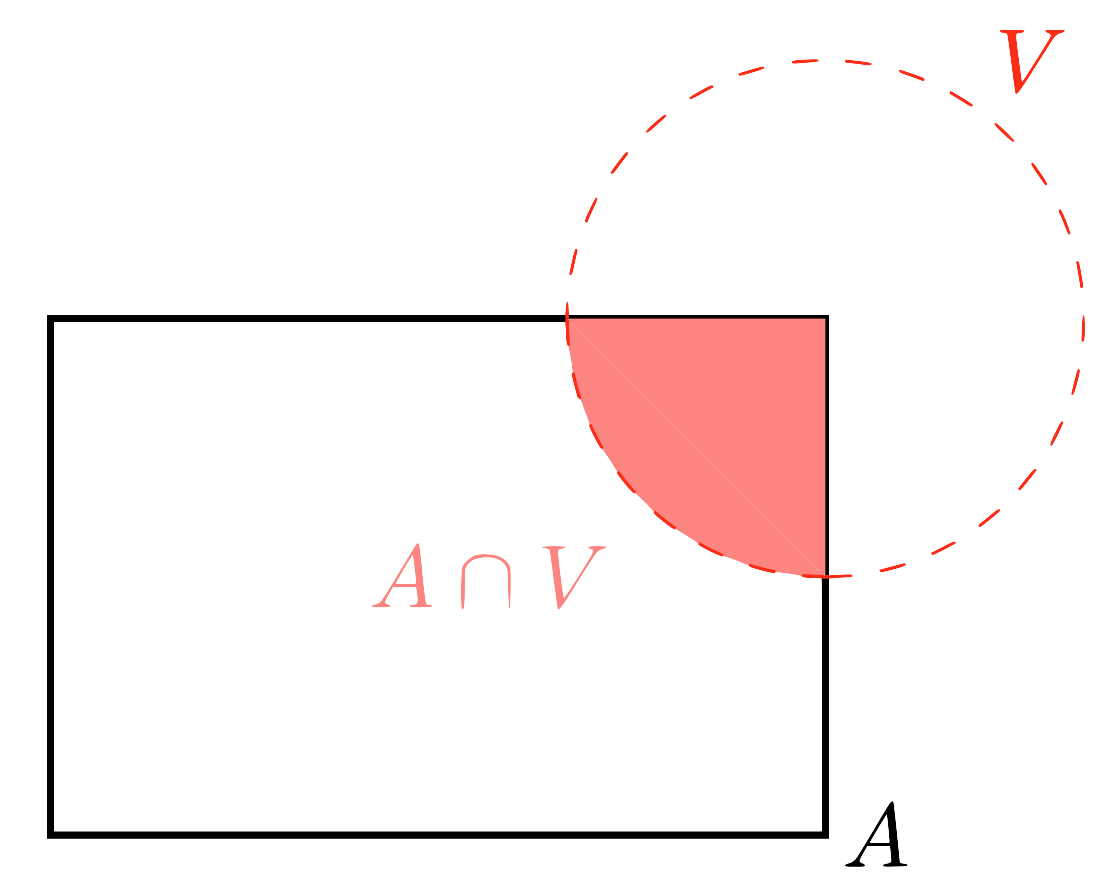
이러한 상황은 $A$가 열린집합이었다면 쉽게 해결된다.

보조정리 2 위상공간 $X$의 부분공간 $A$에 대하여, $A$의 모든 열린집합이 $X$에서도 열린집합일 필요충분조건은 $A$가 $X$의 열린집합인 것이다.

증명

$A$는 $A$에서 열린집합이므로 한쪽 방향은 자명하다.

반대 방향의 경우, $A$의 임의의 열린집합을 택하면 이를 $U\cap A$로 쓸 수 있도록 하는 $X$의 열린집합 $U$가 존재하는데, $A$ 또한 열린집합이므로 $U\cap A$도 열린집합이 된다.

어렵지 않게 부분공간 $A$에서의 닫힌집합은 정확하게 $X$의 닫힌집합 $C$에 대하여, $A\cap C$의 꼴로 나타나는 집합들임을 알 수 있다. 닫힌집합의 경우에도 위의 예시와 같은 상황이 생길 수 있는데, 이를 해결하는 방법 또한 마찬가지로 간단하다.

보조정리 3 위상공간 $X$의 부분공간 $A$에 대하여, $A$의 모든 닫힌집합이 $X$에서도 닫힌집합일 필요충분조건은 $A$가 $X$의 닫힌집합인 것이다.

증명

$A$는 $A$에서 닫힌집합이므로 한쪽 방향은 자명하다.

반대 방향의 경우, $A$의 임의의 닫힌집합을 택하면 이를 $U\cap A$로 쓸 수 있도록 하는 $X$의 닫힌집합 $U$가 존재하는데, $A$ 또한 닫힌집합이므로 $U\cap A$도 닫힌집합이 된다.

우리는 지금까지 모든 위상적 성질을 근방이라는 개념을 통해 정의해왔었는데, 이 또한 위의 보조정리들과 마찬가지로 올바르게 수정해줄 수 있다.

보조정리 4 위상공간 $X$의 부분공간 $A$와 임의의 $x\in A$에 대하여, 모든 $A$에서의 $x$의 근방이 $X$에서도 $x$의 근방일 필요충분조건은 $A$가 $X$에서 $x$의 근방인 것이다.

증명

$A$는 $A$에서 $x$의 근방이므로 한쪽 방향은 자명하다.

반대 방향의 경우, $x$의 $A$에서의 임의의 근방 $U$을 택하자. 그럼 $U$에 포함되는 $x$의 ($A$에서의) 열린근방 $U’$가 존재한다. 한편 $A$가 $X$에서 $x$의 근방이라면, $A$에 포함되는 ($X$에서의) $x$의 열린근방 $V$가 존재한다. 이제 $U’\cap V$는 공집합이 아닌 부분집합이고, $U’\cap V\subseteq V$이고 $U’\cap V$는 $X$에서 $x$의 열린근방이므로 $V$는 $X$에서의 $x$의 근방이다.

이 보조정리들을 통하여 지금까지 살펴본 개념들을 부분공간으로 제한할 수 있다.

명제 5 위상공간 $X$와 부분집합들 $A\subseteq B\subseteq X$를 생각하자. 그럼 $B$에 대한 $A$의 closure $\cl_BA$는

\[\cl_BA=B\cap\cl_XA\]

와 같다.

증명

임의의 $x\in B$에 대하여, $x$의 $B$에서의 근방은 항상 $x$의 $X$에서의 적당한 근방 $V$에 대하여 $V\cap B$의 형태로 쓰여진다. 이제 $V\cap A=(V\cap B)\cap A$와 §집합의 내부, 폐포, 경계, ⁋명제 6을 사용하면 원하는 결과를 얻는다.

따라서 $A\subseteq B\subseteq X$에 대하여, $A$가 $B$의 dense subset인 것은

\[B=\cl_BA=B\cap\cl_XA\]

인 것과 동치이고, 다시 이로부터 $B\subseteq\cl_XA$인 것과 동치임을 알 수 있다.

명제 6 위상공간 $X$와, $X$의 부분집합들 $(A_i)_{i\in I}$가 주어졌다 하고, 다음 두 조건 중 하나가 성립한다 하자.

1. $X=\bigcup_{i\in I}\interior(A_i)$가 성립하거나,
2. $(A_i)_{i\in I}$가 $X$의 locally finite, closed covering이다.

그럼 $X$의 임의의 부분집합 $B$가 $X$에서 열린집합 (resp. 닫힌집합)인 것은 모든 $A_i$에 대하여 $B\cap A_i$가 $A_i$에서 열린집합 (resp. 닫힌집합)인 것과 동치이다.

증명

우선

\[X\setminus B\cap A_i=A_i\setminus (B\cap A_i)\]

으로부터, 이 명제는 열린집합 혹은 닫힌집합 중 하나에 대해서만 보이면 충분하다. 또, $B$가 $X$에서 열린집합이라면 $B\cap A_i$가 $A_i$에서 열린집합인 것은 정의이므로, 이 명제의 핵심은 반대방향이다.

1. $(A_i)$들이 첫 번째 조건을 만족한다 하고, $B\cap A_i$가 $A_i$에서 열린집합임을 가정하자. $A_i$를 전체집합으로 보고, $\interior A_i$를 부분공간으로 본다면 이로부터 $B\cap\interior A_i$가 $\interior A_i$에서 열린집합임을 안다. 이제 $\interior A_i$는 열린집합이므로, 보조정리 2를 적용하면 $B\cap\interior A_i$는 $X$에서 열린집합임을 안다. 따라서

   \[B=B\cap X=B\cap\left(\bigcup_{i\in I} \interior A_i\right)=\bigcup_{i\in I}(B\cap\interior A_i)\]

   으로부터 $B$는 열린집합임을 안다.

2. 이제 $(A_i)$가 두 번째 조건을 만족한다 하자. 이번에는 $B\cap A_i$들이 모두 $A_i$에서 닫힌집합임을 가정한다. 그럼 $B\cap A_i$는 보조정리 3에 의하여 $X$에서 닫힌 집합이다. 이제 $(B\cap A_i)$는 locally finite인 닫힌집합들의 모임이며, $B=\bigcup (B\cap A_i)$이므로 §집합의 내부, 폐포, 경계, ⁋명제 4에 의하여 $B$는 닫힌집합이다.

부분공간과 연속함수

위상공간 $X,Y$와 함수 $f:X\rightarrow Y$가 주어졌다 하자. 그럼 $f(X)\subseteq B\subseteq Y$를 만족하는 집합 $Y$에 대하여, $f$의 공역을 $B$로 제한하여 얻어진 함수는 연속이다. 이는 정의 1과 §Initial topology와 final topology^†, ⁋명제 3에 의하여 자명하다.

이번에는 위와 같은 상황에서, $X$의 부분집합 $A$가 주어졌다 하자. 그럼 $f:X\rightarrow Y$를 $A$로 제한한 함수 $f|_A$는 $\iota:A\hookrightarrow X$에 대하여 $f\circ\iota$와 같다. 이는 연속함수 둘의 합성이므로 자명하게 $f|_A$ 또한 연속임을 확인할 수 있다. 그러나 일반적으로 그 역은 성립하지 않는다.

예시 7 두 위상공간 사이의 함수 $f:X\rightarrow Y$가 연속이 아니라 하자. 임의의 $x\in X$에 대하여, $A=\{x\}$으로 두면 $f|_A$는 연속이다. 이는 $Y$의 임의의 열린집합 $U$에 대하여, $f^{-1}(U)$는 항상 공집합 혹은 $\{x\}$이기 때문이다.

그 대신, 만일 집합 $A$가 $x$의 근방이었다면, $f|_A$가 점 $x\in X$에서 연속이라는 것으로부터 $f$가 $x$에서 연속이라는 것을 유도해낼 수 있다. 보조정리 4에 의하여 $x$의 $A$에서의 근방은 항상 $X$에서의 근방으로 볼 수도 있기 때문이다. 이 논증을 사용하여 함수 $f$가 모든 점에서 연속이라는 것을 보이기 위해서는 임의의 $x\in X$마다 근방 $N(x)$를 잡아 $f|_{N(x)}$가 반드시 연속이라는 것을 증명해야 하지만, 다음 명제에 의하여 이보다 약한 정보만을 갖고서도 $f$가 연속이라는 것을 증명할 수 있다.

명제 8 위상공간 $X$와, 명제 6의 조건 중 하나를 만족하는 부분집합들의 모임 $(A_i)_{i\in I}$가 주어졌다 하자. 그럼 위상공간 $Y$로의 임의의 함수 $f:X\rightarrow Y$가 연속인 것은 $f|_{A_i}$가 모두 연속인 것과 동치이다.

증명

$f|_{A_i}$가 모두 연속이라 가정하고 $f$가 연속이라는 것만 보이면 충분하다. $Y$의 임의의 닫힌집합 $B$를 택하고, $A=f^{-1}(B)$라 하자. $f|_{A_i}$가 모두 연속이므로, $(f|_{A_i})^{-1}(B)=A\cap A_i$는 모두 닫힌집합이다. 이로부터 명제 6을 적용하면 $A$가 닫힌집합임을 알 수 있고, 따라서 $f$는 연속이다.