카테고리 $\Ch(\mathcal{A})$
[범주론] §아벨 카테고리에서 우리는 chain complex들의 카테고리 $\Ch(\mathcal{A})$가 존재하며, abelian category가 된다는 것을 언급하였는데, 이번 절에서 우리는 조금 더 구체적으로 이 주장을 살펴본다. 우선 $\Ch(\mathcal{A})$에서의 morphism은 다음과 같이 주어진다.
정의 1 두 chain complex $C_\bullet, D_\bullet$에 대하여, 이들 사이의 chain map사슬변환 $f_\bullet:C_\bullet\rightarrow D_\bullet$은 다음의 diagram
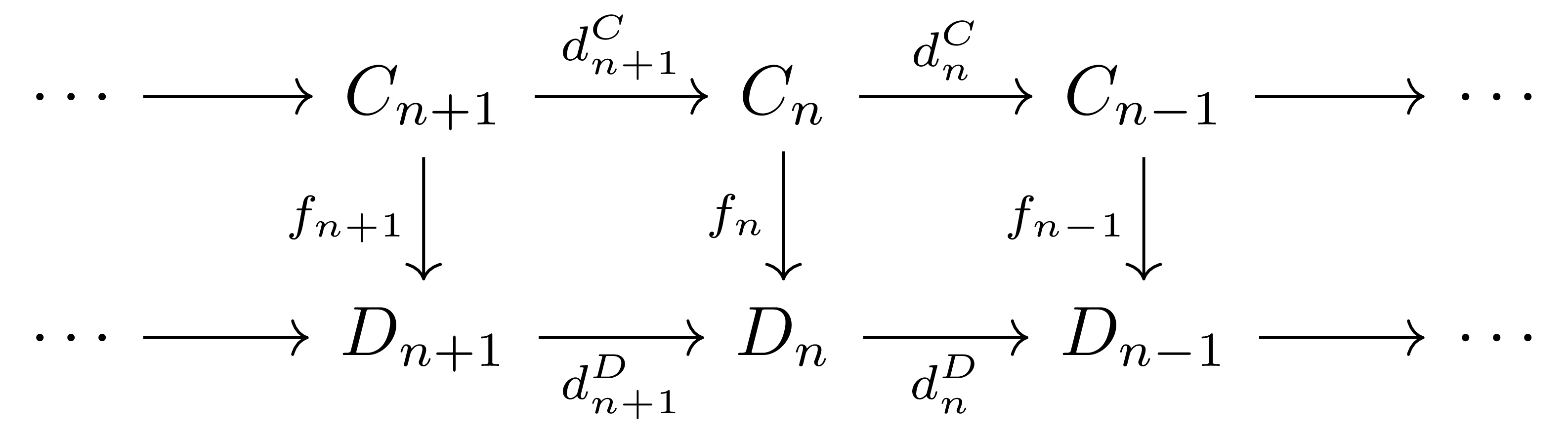
을 commute하도록 하는 $f_n:C_n\rightarrow D_n$들의 모임이다.
즉, $f_\bullet$이 chain map이라는 것은 모든 $n$에 대하여
\[f_{n-1}\circ d_n^C=d_n^D\circ f_n\]이 성립하는 것이다. 혼동의 여지가 없을 때에는 $d^C$와 $d^D$를 모두 $d$로만 적는다. 그럼 category $\Ch(\mathcal{A})$를
- $\mathcal{A}$의 chain complex들의 모임 $\obj(\Ch(\mathcal{A}))$,
- Chain complex $C_\bullet$에서 $D_\bullet$으로의 chain map들의 모임 $\Mor_{\Ch(\mathcal{A})}(C_\bullet,D_\bullet)$
으로 정의하면 $\Ch(\mathcal{A})$가 category가 된다는 것이 자명하다. 이 때, $\id_{C_\bullet}$은 모든 $n$에 대하여 $\id_n:C_n\rightarrow C_n$이 $\id_{C_n}$으로 정의된 $\id_\bullet:C_\bullet\rightarrow C_\bullet$이며, chain map들의 합성은
\[g_\bullet\circ f_\bullet=(g_n\circ f_n)_{n\in\mathbb{Z}}\]으로 주어진다.
뿐만 아니라, category $\Ch(\mathcal{A})$는 $\Ab$-category이다. 두 chain map $f_\bullet,g_\bullet:C_\bullet\rightarrow D_\bullet$이 주어졌다면 이들의 합을
\[f_\bullet+g_\bullet=(f_n+g_n)_{n\in\mathbb{Z}}\]으로 정의하면 $\Mor_{\Ch(\mathcal{A})}(C_\bullet,D_\bullet)$이 abelian group이 되고, 또 두 chain complex $C_\bullet,D_\bullet$이 주어진다면 이들의 곱 $C_\bullet\oplus D_\bullet$은1 다음의 chain complex
\[C_\bullet\oplus D_\bullet:\quad \cdots \longrightarrow C_{n+1}\oplus D_{n+1}\overset{d_{n+1}^C\oplus d_{n+1}^D}{\longrightarrow}C_n\oplus D_n\overset{d_{n}^C\oplus d_{n}^D}{\longrightarrow}C_{n-1}\oplus D_{n-1}\longrightarrow\cdots\]으로 정의하면 되기 때문이다. Zero object는 다음의 chain complex
\[\cdots\rightarrow 0\rightarrow 0\rightarrow 0\rightarrow\cdots\]이다.
이제 $\Ch(\mathcal{A})$가 abelian category라는 것을 보이기 위해서는 임의의 chain map $f_\bullet:C_\bullet \rightarrow D_\bullet$의 kernel과 cokernel을 정의하면 충분하다. 우선 각각의 $n$에 대하여, $f_n:C_n \rightarrow D_n$은 abelian category $\mathcal{A}$에서의 morphism이므로 $i_n:\ker f_n\rightarrow C_n$과 $p_n:D_n\rightarrow \coker f_n$을 갖는다. 다음의 diagram
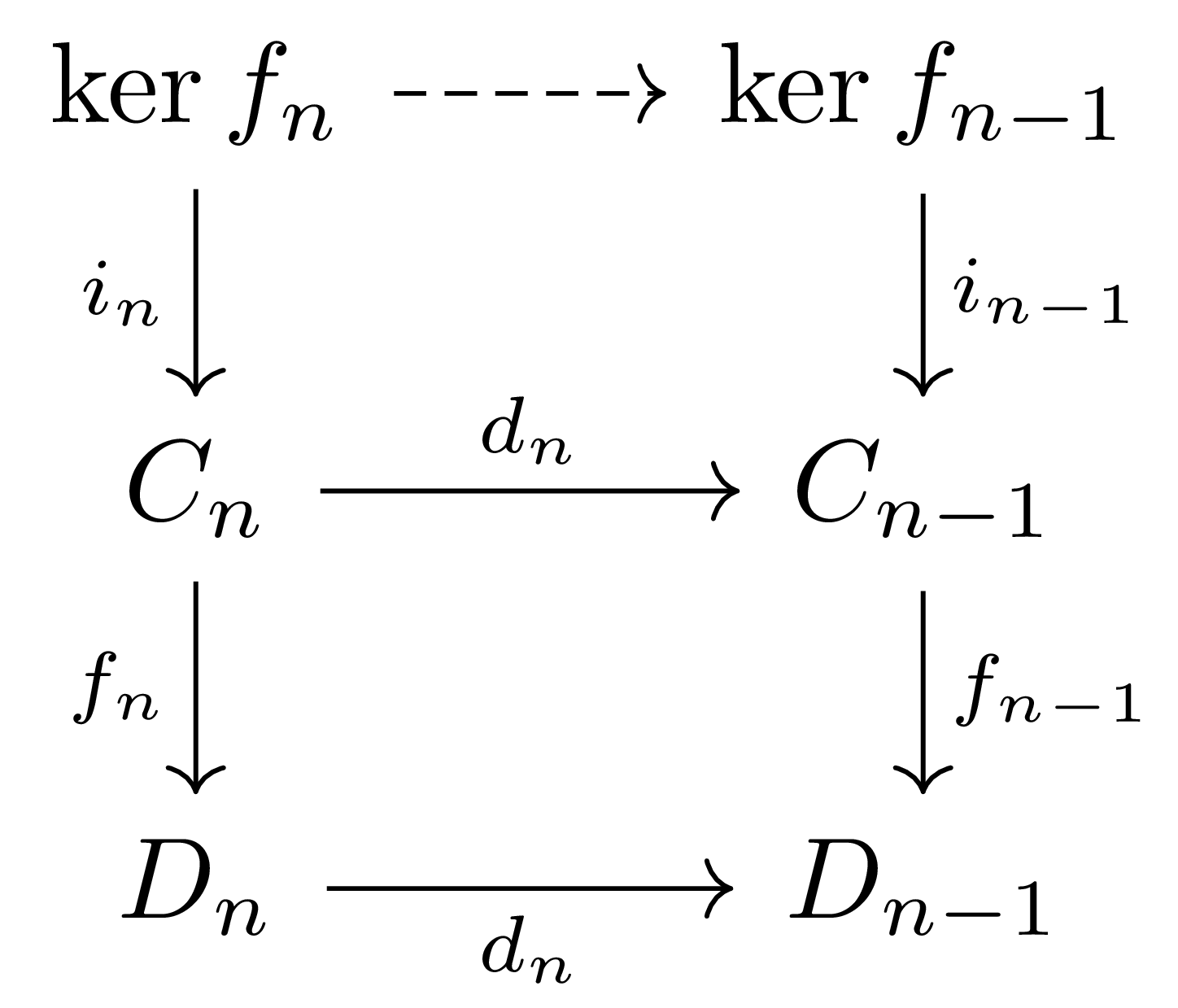
을 생각하자. 그럼
\[f_{n-1}\circ d_n\circ i_n=d_n\circ f_n\circ i_n=0\]이므로, $\ker f_{n-1}$의 universal property로부터 morphism $\ker f_n\rightarrow \ker f_{n-1}$이 자연스럽게 유도된다. 비슷하게 $\coker f_n\rightarrow \coker f_{n-1}$ 또한 정의되며, 이 정보들은 각각 두 chain complex
\[\ker(f_\bullet):\qquad \cdots\longrightarrow \ker f_{n+1}\longrightarrow \ker f_n\longrightarrow \ker f_{n-1}\longrightarrow\cdots\]과
\[\coker(f_\bullet):\qquad \cdots\longrightarrow \coker f_{n+1}\longrightarrow \coker f_n\longrightarrow \coker f_{n-1}\longrightarrow\cdots\]을 각각 구성한다. 이렇게 정의한 $\ker(f_\bullet)$이 $\Ch(\mathcal{A})$에서 $f_\bullet$의 kernel이 된다는 것을 보이기 위해서는 다음의 universal property
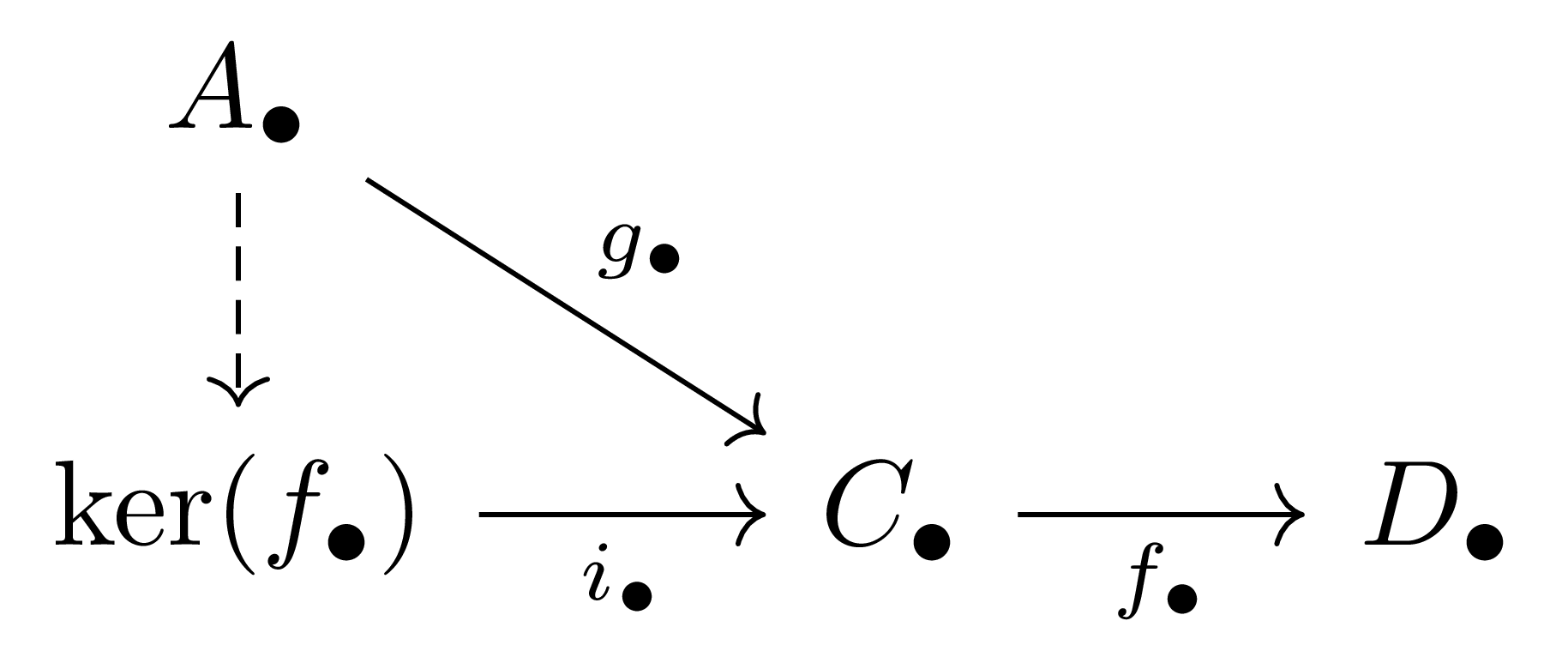
을 보여야 하는데, 다시 이를 위해서는 우선 각각의 $n$에 대하여 다음 diagram
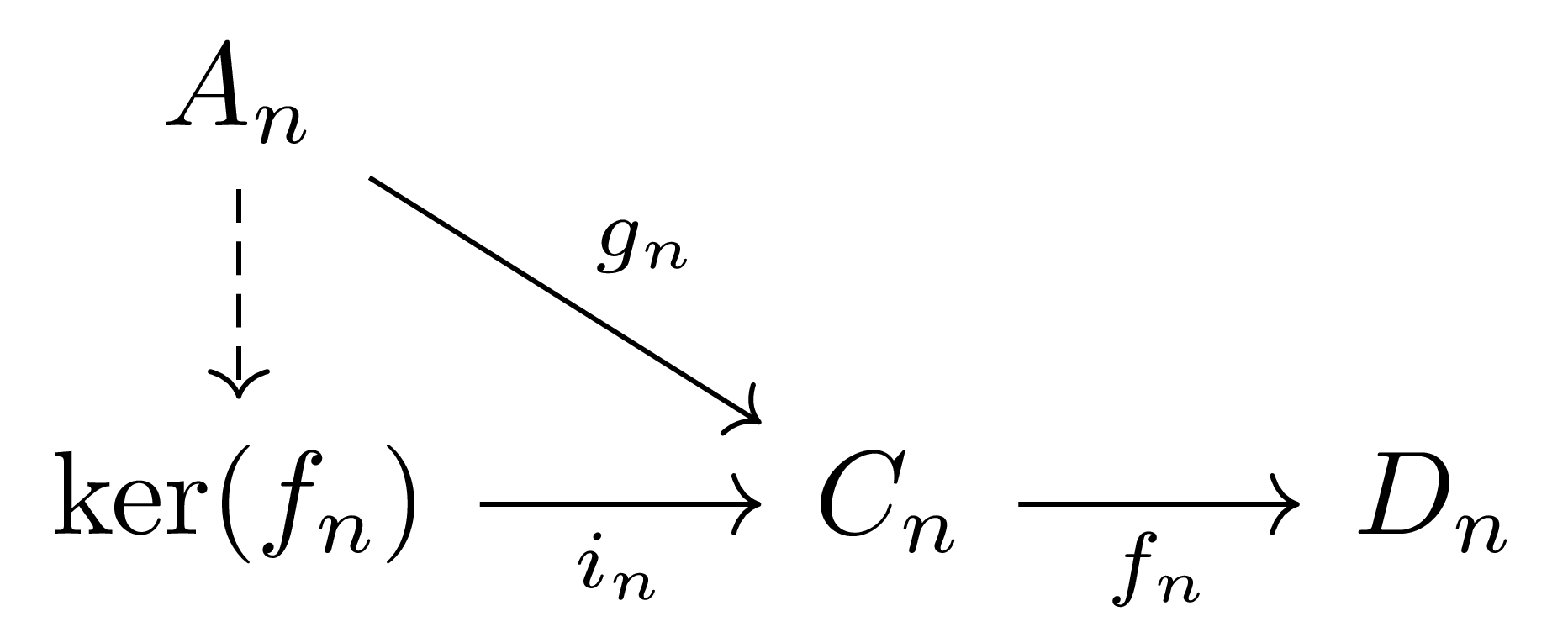
을 통해 $j_n:A_n\rightarrow \ker f_n$을 만든 후, $j_\bullet$이 chain map임을 보이면 충분하다. 즉, 다음 diagram
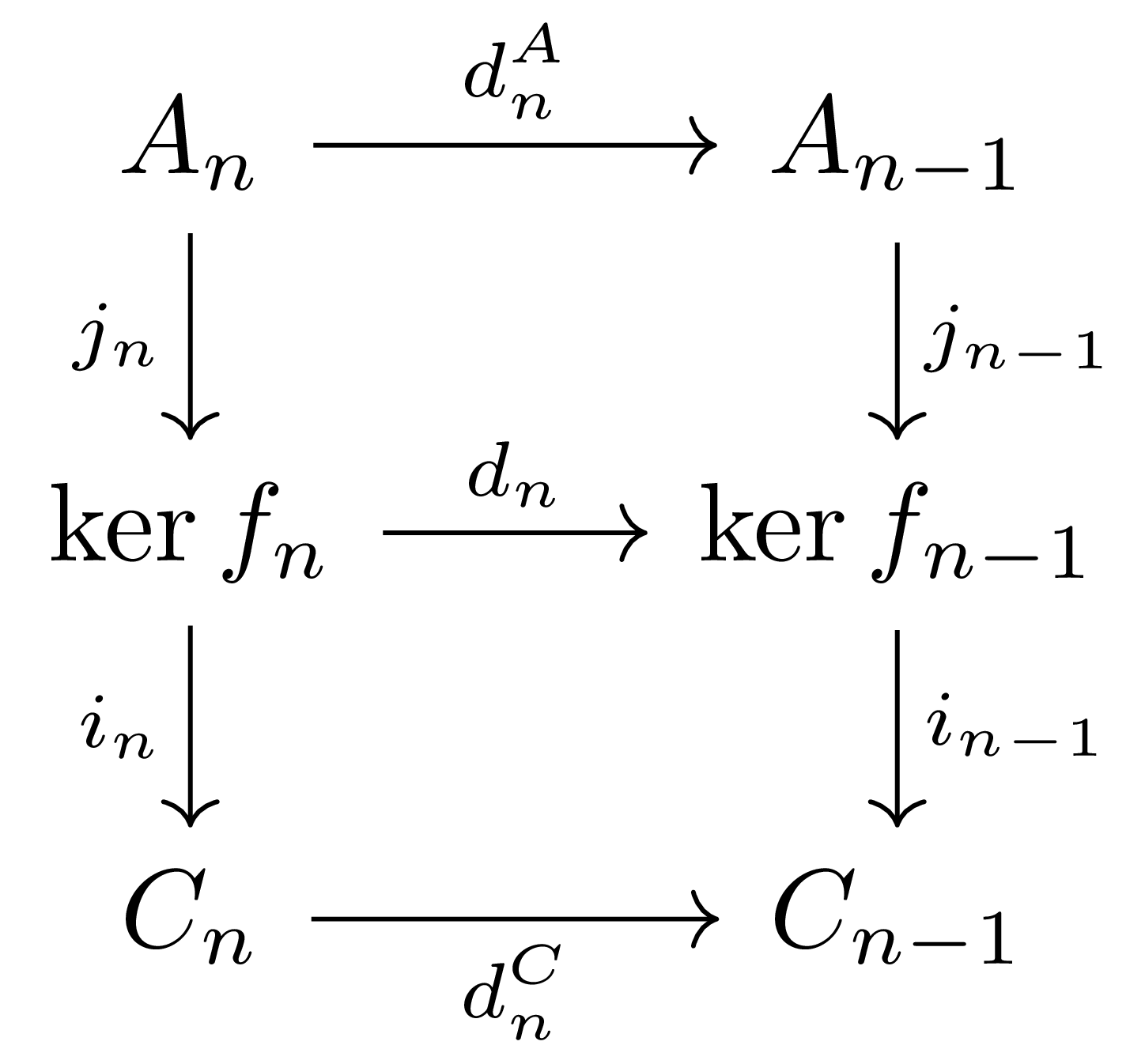
의 위쪽 사각형이 commute한다는 것을 증명하면 된다. 그런데 kernel은 항상 monomorphism이므로, 이를 위해서는
\[i_{n-1}\circ(j_{n-1}\circ d_n^A)=i_{n-1}\circ(d_n\circ j_n)\]이 성립한다는 것만 보이면 충분하고, 이는 정의에 의해 자명하므로 $\ker(f_\bullet)$은 실제로 $f_\bullet$의 kernel이 된다. 비슷하게 $\coker(f_\bullet)$이 $\Ch(\mathcal{A})$에서 $f_\bullet$의 cokernel이 된다는 것을 확인할 수 있다.
마지막으로 임의의 monomorphism $f_\bullet$이 $\ker(\coker f_\bullet)$와 같고, 임의의 epimorphism $f_\bullet$은 $\coker(\ker f_\bullet)$와 같다는 것을 보여야 한다. 이는 우선 $f_\bullet$이 monomorphism (resp. epimorphism)인 것과, 모든 $n$에 대하여 $f_n$이 monomorphism (resp. epimorphism)인 것이 동치임을 증명한 후, 각 차수별로 abelian category의 조건을 사용한 후 합쳐주면 된다. 이 과정은 위와 거의 동일하므로, 자세한 논증은 생략하기로 한다.
호몰로지
Chain complex $C_\bullet$을 고정하고, 새로운 chain complex $C_{\bullet-1}$을
\[C_{\bullet-1}:\qquad\cdots\longrightarrow\underbrace{C_n}_\text{\small degree $n+1$}\overset{d_n}{\longrightarrow}\underbrace{C_{n-1}}_\text{\small degree $n$}\overset{d_{n-1}}{\longrightarrow}\underbrace{C_{n-2}}_\text{\small degree $n-1$}\longrightarrow\cdots\tag{1}\]으로 정의하자. 즉 $C_{\bullet-1}$은 $C_\bullet$을 한 칸씩 옮겨서 얻어지는 chain complex이다. 이제 chain map $d_\bullet:C_\bullet\rightarrow C_{\bullet-1}$을 다음의 diagram

와 같이 정의하자. 그럼 $\ker (d_\bullet)$이 잘 정의되며, 다음의 diagram
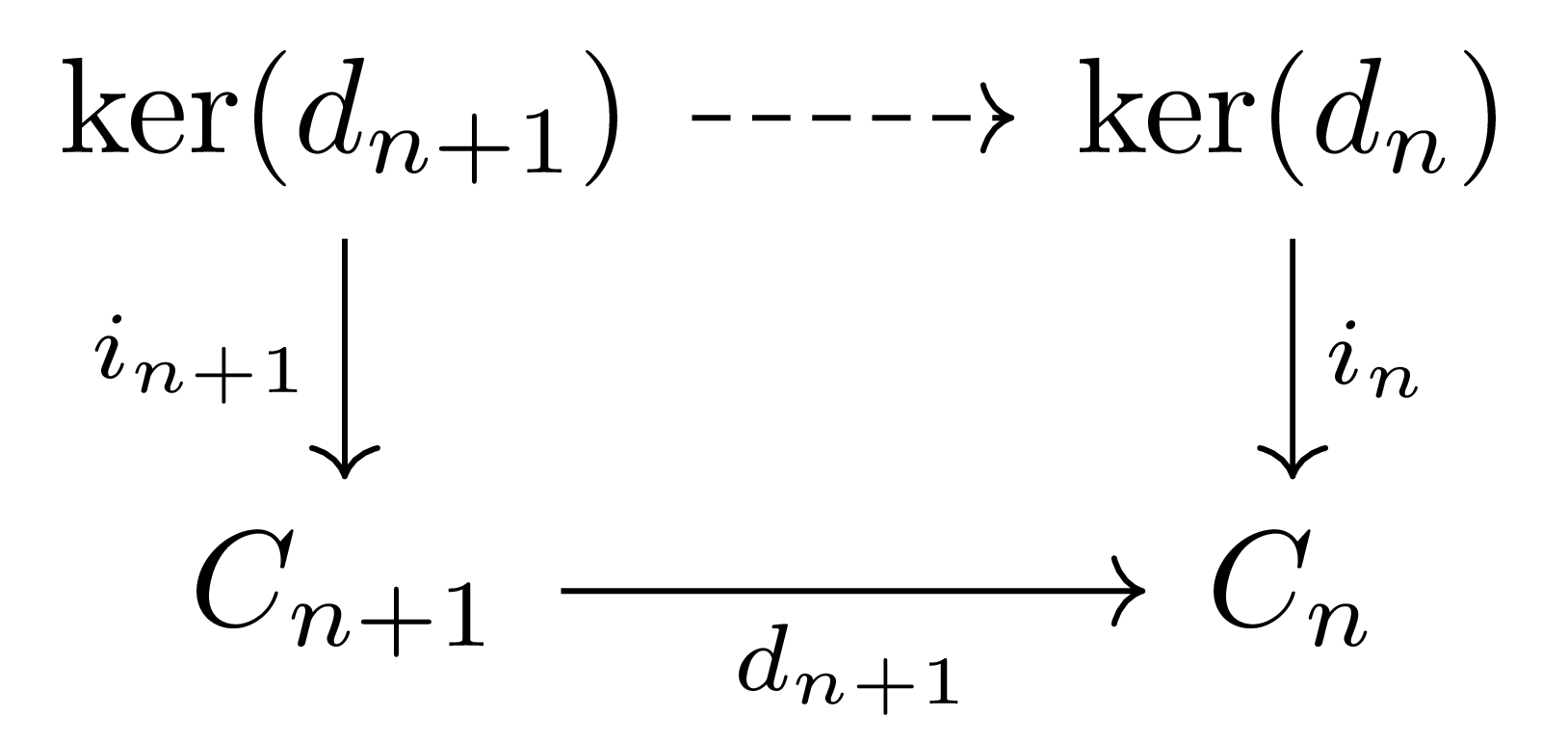
을 고려하면 $d_{n+1}\circ i_{n+1}=0$인 것과 $i_n$이 monomorphism인 것으로부터 $\ker(d_\bullet)$의 differential은 모두 zero map임을 알 수 있다.
마찬가지로 $\coker(d_\bullet)$ 또한 잘 정의되며, 이들 사이의 differential 또한 0이 된다. 위에서 살펴본 $\ker(d_\bullet)$의 $n$번째 성분이 $\ker d_n\rightarrow C_n$인 것과는 달리, $\coker(d_\bullet)$의 $n$번째 성분은 $C_{n-1}\rightarrow \coker(d_n)$이므로 약간의 혼동이 있을 수 있으므로 우리는 다시 차수를 하나씩 옮겨서 chain complex $\coker(d_{\bullet+1})$를 생각한다.
이제
\[\im(d_{\bullet+1})=\ker(C_\bullet\rightarrow \coker(d_{\bullet+1}))\]으로 생각하고, $\ker(d_\bullet)\rightarrow C_\bullet$의 universal property를 사용하면 monomorphism
\[\im(d_{\bullet+1})\rightarrow\ker(d_\bullet)\]을 얻고, 이를 통해 새로운 chain complex
\[H_\bullet(C)=\ker(d_\bullet)/\im(d_{\bullet+1})\]을 얻는다.
명시적으로 $H_n(C)$는 다음의 diagram
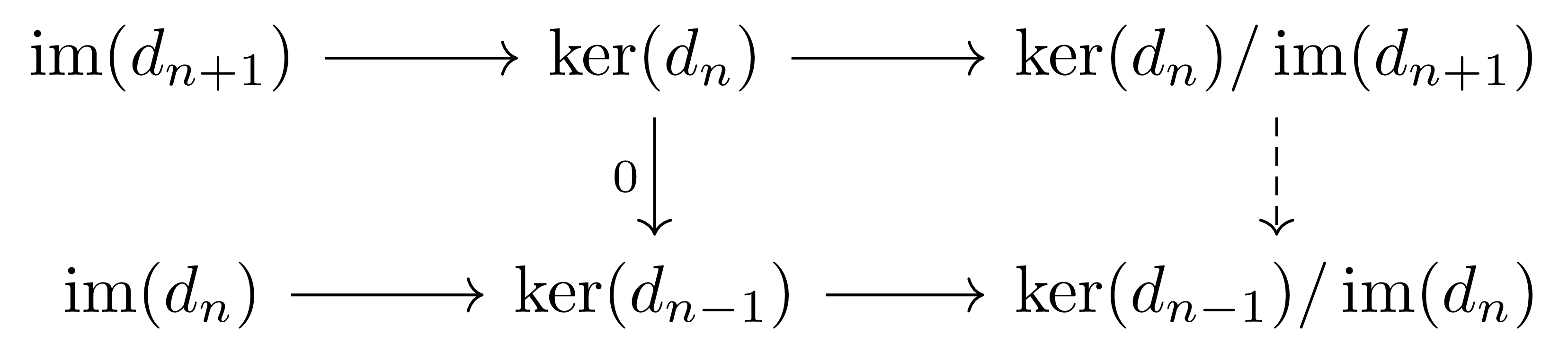
을 통해 유도된다. 그런데 $\ker(d_n)\rightarrow H_n$은 epimorphism이고, $\ker(d_n)\rightarrow\ker(d_{n-1})$이 $0$이므로 $H_n(C)\rightarrow H_{n-1}(C)$ 또한 zero map이다. 이는 ($\ker(d_\bullet)$이나 $\coker(d_\bullet)$과 마찬가지로) $H_\bullet(C)$가 chain complex로서는 크게 의미가 없고, 대신 $H_\bullet(C)$의 각각의 성분인 $H_n(C)\in\obj(\mathcal{A})$들이 흥미로운 대상임을 보여준다.
정의 3 임의의 chain complex
\[C_\bullet:\quad\cdots\overset{d_{n+2}}{\longrightarrow} C_{n+1}\overset{d_{n+1}}{\longrightarrow} C_n\overset{d_n}{\longrightarrow} C_{n-1}\overset{d_{n-1}}{\longrightarrow}\cdots\]에 대하여, $C_\bullet$의 $n$-cycle들의 module은 $Z_n(C)=\ker (d_n)$으로 주어진다. 또, $\im(d_{n+1})$을 $C_\bullet$의 $n$-boundary들의 module이라 부르고, $B_n(C)$으로 적는다. 이 때, $C_\bullet$의 $n$번째 호몰로지$n$-th homology는 $H_n(C)=Z_n(C)/B_n(C)$로 정의된다.
비슷하게 cochain complex에 대해서는 $n$-cocycle과 $n$-coboundary, 그리고 $n$번째 코호몰로지가 정의된다.
$H_\bullet$ 자체는 $\Ch(\mathcal{A})$에서 $\Ch(\mathcal{A})$로의 functor지만, 각각의 성분 $H_n$은 $\Ch(\mathcal{A})$에서 $\mathcal{A}$로의 functor를 정의한다.
명제 4 임의의 $n$에 대하여, $H_n$은 $\Ch(\mathcal{A})$에서 $\mathcal{A}$로의 functor이다.
증명
임의의 chain map $f_\bullet:C_\bullet\rightarrow D_\bullet$에 대하여, §Diagram chasing, ⁋보조정리 4를 적용하면 $f_n$이 $Z_n(C)\rightarrow Z_n(D)$, $B_n(C)\rightarrow B_n(D)$을 각각 유도한다는 것을 안다. 따라서 $f_n$은
\[H_n(f):H_n(C)\rightarrow H_n(D)\]을 유도한다. 이렇게 얻어지는 데이터들이 functor를 구성한다는 것을 확인하면 되는데, 이는 모두 자명하다.
Double complex와 translation
마지막으로 double complex를 정의한다. 직관적으로 이는 abelian category $\Ch(\mathcal{A})$들로 이루어진 chain complex, 즉 $\Ch(\Ch(\mathcal{A}))$의 대상이라 생각할 수 있다. 위에서 살펴본 (1)의 chain complex $C_{\bullet-1}$과 그 밑의 chain map이 그 예시이다.
그러나 나중에 계산을 할 때 각 행의 부호가 바뀌도록 해주면 더 깔끔한 결과를 얻을 때가 있다.2 이러한 sign convention을 받아들여 다음과 같이 정의한다.
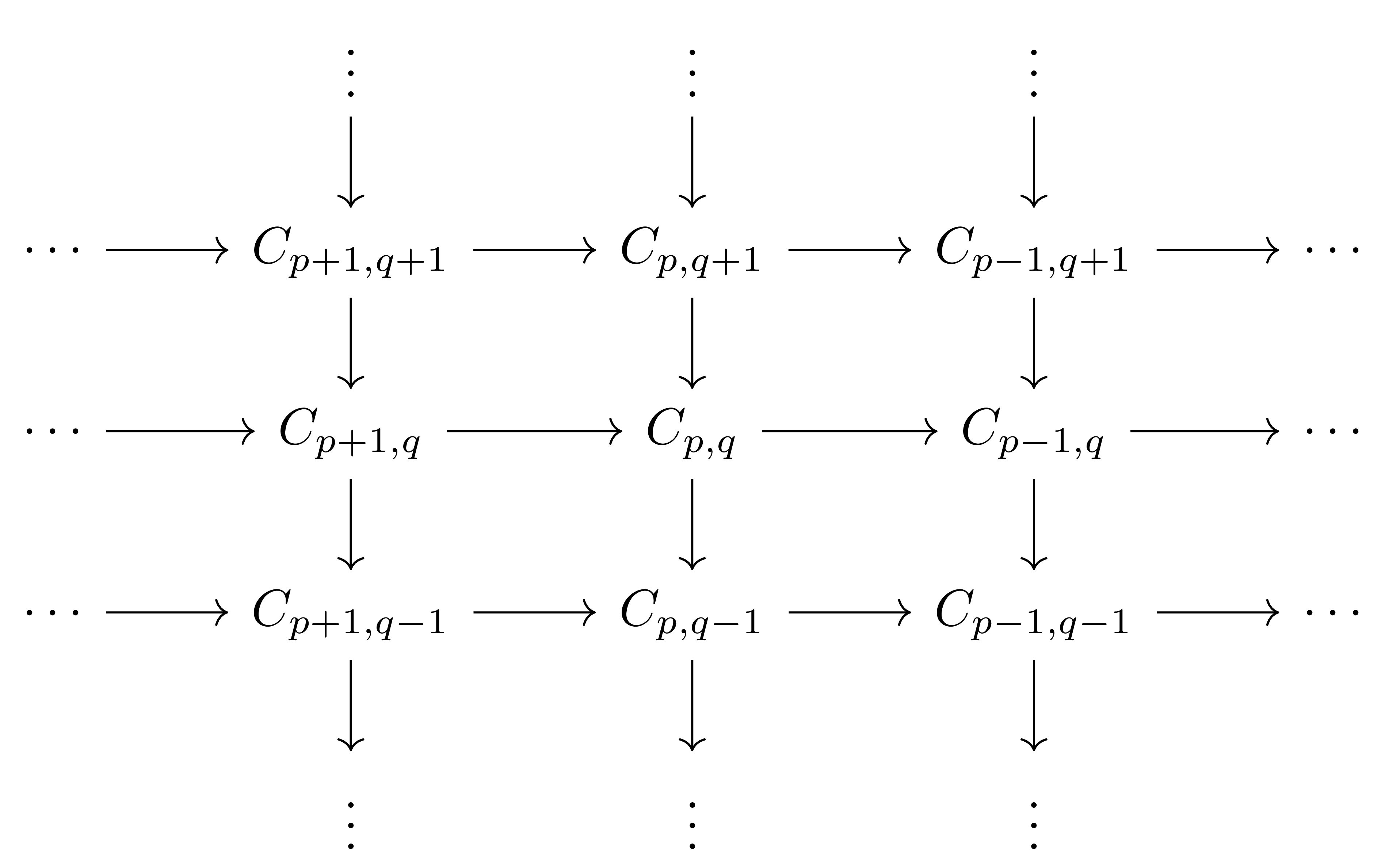
정의 5 Abelian category $\mathcal{A}$의 대상들로 이루어진 double complex는 다음의 두 함수들
\[d^h:C_{p,q}\rightarrow C_{p-1,q},\qquad d^v:C_{p,q}\rightarrow C_{p,q-1}\]이 주어진 대상이며, 이들은
\[(d^h)^2=(d^v)^2=d^vd^h+d^hd^v=0\]을 만족한다.
조건 $d^vd^h+d^hd^v=0$은 $d^vd^h=-d^hd^v$를 의미하므로 double complex들은 $\mathbf{Ch}(\mathbf{Ch}(\mathcal{A}))$의 대상이 아니지만, $d^v$로부터 다음의 식
\[f_{p,q}=(-1)^pd_{p,q}^v:C_{p,q}\rightarrow C_{p,q-1}\]을 정의하면 이를 $\mathbf{Ch}(\mathbf{Ch}(\mathcal{A}))$의 대상으로 취급할 수 있다.
Double complex를 정의할 때 위와 같은 sign convention을 사용했으므로, $C$의 $p$-th translation $C[p]$ 또한 다음의 식
\[C[p]_n=C_{n+p}\]으로 주어진 chain complex이며, 이 때의 differential은 $(-1)^pd$으로 정의해야 한다. 예컨대 $C[-1]$은 위에서 정의한 $C_{\bullet-1}$과 동일하지만, 각 differential들의 부호가 바뀐 chain complex를 의미한다.
어쨌든 이렇게 새로 생겨난 부호와는 관계없이
\[H_n(C[p])=H_{n+p}(C)\]임이 자명하며, 또 만일 $f:C\rightarrow D$가 chain map이라면 $f[p]$를 다음의 식
\[f[p]_n=f_{n+p}\]으로 정의하여 $f[p]:C[p]\rightarrow D[p]$을 만들 수 있다. 즉 translation은 $\mathbf{Ch}(\mathcal{C})$에서 자기 자신으로의 functor이다.
Truncation
마지막으로 임의의 chain complex $C_\bullet$가 주어졌다 하자. 임의의 정수 $n$에 대하여, 다음의 식
\[(\tau_{\geq n}C)_i=\begin{cases}0&\text{if $i < n$}\\ Z_n&\text{if $i=n$}\\ C_i&\text{if $i > n$}\end{cases}\]그리고 $C_\bullet$와 동일한 differential로 정의된 chain complex $(\tau_{\geq n}C)_\bullet$를 intelligent truncation이라 부른다. 그럼
\[H_i(\tau_{\geq n}C)=\begin{cases}0&\text{if $i < n$}\\ H_i(C)&\text{if $i\geq n$}\end{cases}\]이 된다. 비슷하게 $(\tau_{< n}C)_\bullet$ 또한 정의할 수 있다. 한편 Brutal truncation은 다음의 식
\[(\sigma_{\geq n}C)_i=\begin{cases}0&\text{if $i \leq n$}\\ C_i&\text{otherwise}\end{cases}\]으로 정의된다. 정의 자체는 $(\sigma_{\geq n}C)_\bullet$가 더 자연스러워보일 수 있지만, $n$번째 호몰로지를 살펴보면 intelligent truncation이 더 좋은 연산을 준다는 것을 확인할 수 있다.
참고문헌
[Wei] C.A. Weibel. An Introduction to Homological Algebra. Cambridge Studies in Advanced Mathematics. Cambridge University Press, 1995.
[Hu] S.T. Hu, Introduction to homological algebra. University Microfilms, 1979.
-
여기에서 $\oplus$는 $\mathcal{A}$에서의 coproduct인 것으로 이해한다. Abelian category에서
유한한 대상들의 product와 coproduct는 일치한다는 것을 증명할 수 있으므로, 사실 $A\oplus B\cong A\times B$이다. ↩ -
예를 들어, Dolbeault operator $d=\partial+\bar{\partial}$의 경우 $d^2=0$은 $0=\partial^2+(\partial\bar{\partial}+\bar{\partial}\partial)+\bar{\partial}^2$와 같으며, bidegree를 고려해주면 $\partial\bar{\partial}+\bar{\partial}\partial=0$임을 안다. ↩

댓글남기기