$\delta$-functor
우리는 앞서 $\Ch(\mathcal{A})$의 임의의 short exact sequence
\[0\longrightarrow A_\bullet\longrightarrow B_\bullet\longrightarrow C_\bullet\longrightarrow 0\]이 주어지면, 이를 통해 long exact sequence
\[\cdots\rightarrow H_n(A)\rightarrow H_n(B)\rightarrow H_n(C)\rightarrow H_{n-1}(A)\rightarrow \cdots\]를 만들 수 있다는 것을 증명했었다. 이 증명의 가장 핵심적인 부분은 connecting map $\delta$를 정의하는 부분인데, 이 과정을 일반화하여 다음과 같이 정의한다.
정의 1 두 abelian category $\mathcal{A},\mathcal{B}$가 주어졌다 하자. 그럼 $\mathcal{A}$에서 $\mathcal{B}$로의 homological $\delta$-functor는 additive functor들 $T_n:\mathcal{A}\rightarrow\mathcal{B}$ ($n\geq 0$), 그리고 임의의 short exact sequence
\[0\longrightarrow A\longrightarrow B\longrightarrow C\longrightarrow 0\]마다 정의된 morphism들 $\delta_n:T_n(C)\rightarrow T_{n-1}(A)$을 의미한다. $n<0$인 경우, $T_n$을 모두 $0$인 것으로 생각한다. 이들은 다음 조건을 만족한다.
-
(Long exact sequence) 다음의 sequence
\[\cdots\longrightarrow T_{n+1}(C)\overset{\delta}{\longrightarrow}T_n(A)\longrightarrow T_n(B)\longrightarrow T_n(C)\overset{\delta}{\longrightarrow}T_{n-1}(A)\longrightarrow \cdots\]가 exact이다.
-
(Naturality) Short exact sequence들 사이의 homomorphism
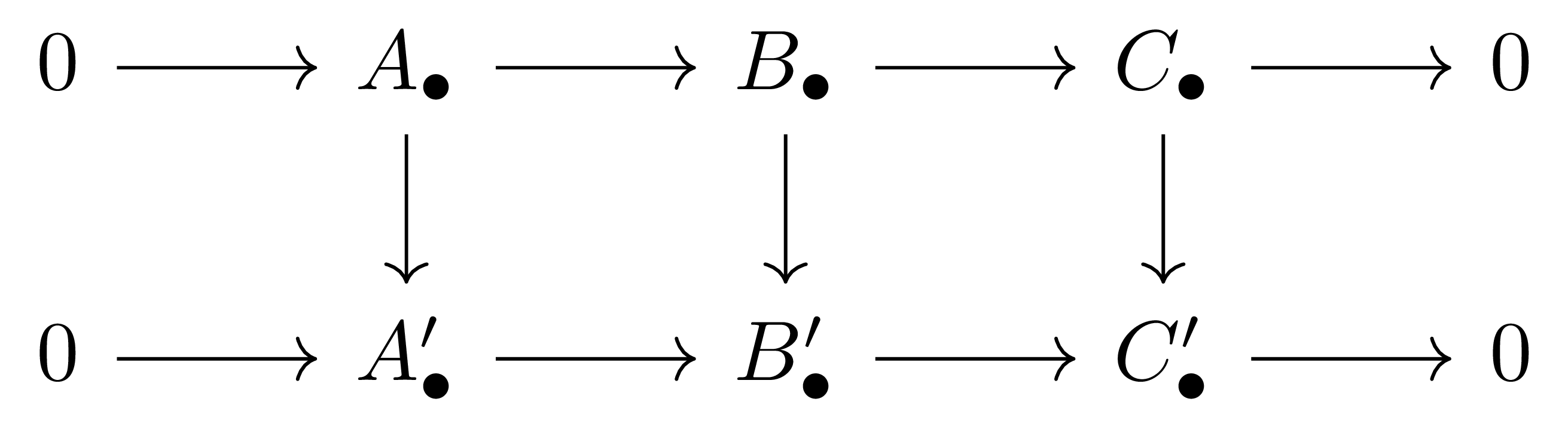
이 주어졌을 때, 다음의 diagram
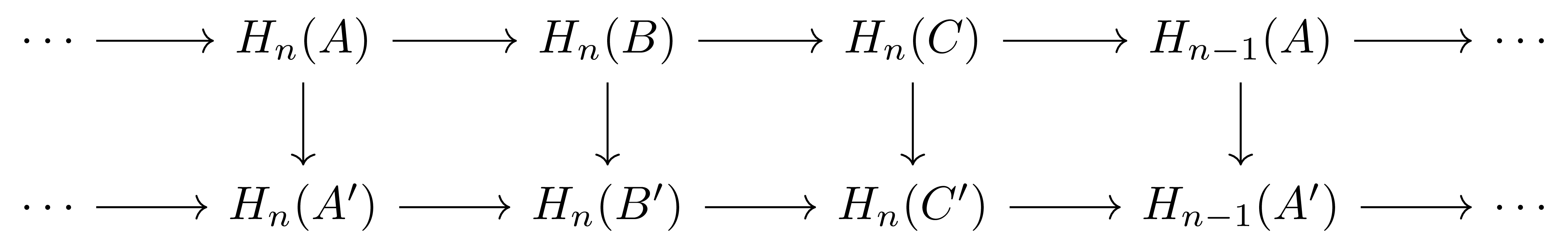
이 commute한다.
위의 정의를 $T^n$들, 그리고 $\delta^n:T^n(C)\rightarrow T^{n+1}(A)$로 바꾸어 쓰면 cohomological $\delta$-functor의 정의를 얻는다. 우리는 $n<0$일 경우, $T_n$과 $T^n$이 모두 $0$인 것으로 생각하기로 하였으므로 homological $\delta$-functor의 첫 번째 조건은 특히
\[\cdots\longrightarrow T_0(A)\longrightarrow T_0(B)\longrightarrow T_0(C)\longrightarrow0\longrightarrow 0\longrightarrow\cdots,\]즉 $T_0$이 right exact functor라는 의미가 된다. 마찬가지로 cohomological $\delta$-functor의 첫 번째 조건은 $T^0$이 left exact functor가 되도록 한다.
또, $\delta$-functor의 두 번째 조건인 naturality는 short exact sequence들의 모임 $\mathbf{S}(\mathcal{A})$에서 $\mathcal{A}$로 가는 두 functor $T_i(C)$와 $T_{i-1}(A)$를 생각할 때, $\delta_i$가 이들 사이의 natural transformation이 된다는 것을 의미한다.
언제나와 같이 cohomological $\delta$-functor의 경우는 homological $\delta$-functor로부터 쉽게 유도할 수 있으므로, 앞으로는 homological $\delta$-functor에 대해서만 생각하기로 한다.
정의 2 두 $\delta$-functor들 $S,T$가 주어졌다 하자. 그럼 $S$에서 $T$로의 morphism $S\rightarrow T$는 $S_n$에서 $T_n$으로의 natural transformation들의 모임들 중, $\delta$와 commute하는 것들을 의미한다.
즉 다음의 diagram이 모든 short exact sequence
\[0\longrightarrow A\longrightarrow B\longrightarrow C\longrightarrow 0\]마다 commute하도록 하는 $\alpha_n:S_n\Rightarrow T_n$들의 모임이다.
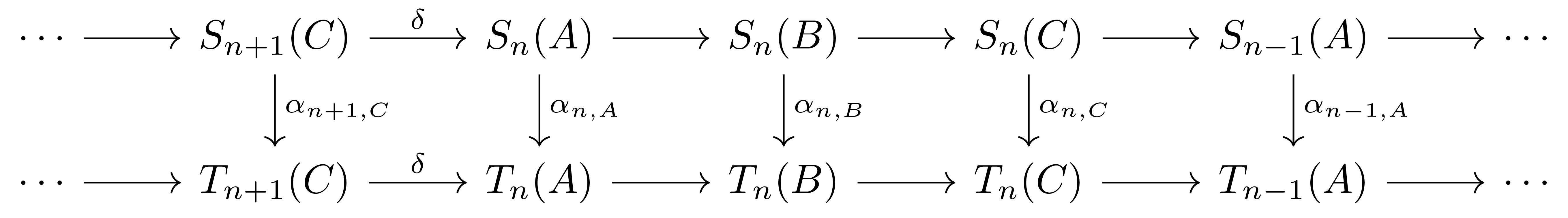
정의 3 임의의 $\delta$-functor $T$가 universal $\delta$-functor라는 것은 임의의 $\delta$-functor $S$와 natural transformation $\alpha_0:S_0\rightarrow T_0$이 주어질 때마다, 이를 확장하는 유일한 $\delta$-functor들 사이의 morphism $(\alpha_n:S_n\Rightarrow T_n)$이 존재하는 것이다.
유도함자
두 abelian category $\mathcal{A},\mathcal{B}$ 사이의 right exact functor $F: \mathcal{A}\rightarrow \mathcal{B}$를 생각하자. 그럼 $\mathcal{A}$는 left exactness를 보존하지 않는다. 가령 $F$가 covariant functor였다 하면, 다음의 short exact sequence
\[0 \rightarrow A_1 \rightarrow A_2 \rightarrow A_3 \rightarrow 0\]이 주어지더라도, 오직 다음의 sequence
\[F(A_1) \rightarrow F(A_2) \rightarrow F(A_3)\rightarrow 0\]의 exactness만이 보존된다. 마찬가지로 left exact functor는 right exactness를 보존하지 않는다.
Derived functor의 철학은 이와 같이 왼쪽 혹은 오른쪽에서 손실되는 정보를 무한히 많은 항들을 이용해 보충하는 것이다. 즉 right exact functor $F$에 대하여, 우리는 $T_0=F$를 만족하는 homological $\delta$-functor들을 찾는 것이 목표이며, 비슷하게 left exact functor에 대해서는 cohomological $\delta$-functor들을 찾는 것이 목표이다.
정의 4 Right exact functor $F:\mathcal{A}\rightarrow \mathcal{B}$가 주어졌다 하고, $\mathcal{A}$가 enough projective를 갖는다 하자. 그럼 $F$의 left derived functor왼쪽 유도함자들 $L_iF$를 다음의 식
\[(L_iF)(A)=H_i(F(P_\bullet)),\qquad\text{$P_\bullet$ a projective resolution of $A$}\]으로 정의한다.
이 정의가 말이 되기 위해서는 $L_iF(A)$가 위에서 선택한 $P_\bullet$의 선택에 의존하지 않아야 한다.
보조정리 5 $L_iF(A)$가 위에서 선택한 $P_\bullet$의 선택에 의존하지 않는다.
증명
두 개의 projective resolution들을 두고, §분해, ⁋정리 6을 identity map에 대해 적용하면 된다.
이제 left derived functor를 조금 더 자세히 살펴보자. 우선 $F$가 right exact인 것으로부터 다음 sequence
\[F(P_1) \overset{Fd_1}{\longrightarrow} F(P_0) \overset{F\epsilon_0}{\longrightarrow} F(A) \longrightarrow 0\]가 exact임을 안다. 따라서
\[L_0F(A)=H_i(F(P))=\frac{F(P_0)}{\im Fd_1}=\frac{F(P_0)}{\ker F\epsilon_0}\cong F(A)\]을 얻는다.
$L_\bullet F$들이 homological $\delta$-functor임을 보이기 위해서는 우선 이들이 additive functor임을 보이고, connecting map $\delta$들을 만들어야 한다. 이를 두 스텝으로 나눈다.
보조정리 6 $L_iF$들은 additive functor이다.
증명
우선 임의의 $f: A’ \rightarrow A$와 $A’$, $A$의 projective resolution들이 각각 주어졌을 때 §분해, ⁋정리 6을 적용하여 $L_nF(f)$를 얻을 수 있다. 이것이 functoriality와 additivity를 만족한다는 것은 universal property로부터 자명하다.
보조정리 7 $L_iF$들은 homological $\delta$-functor이다.
증명
우선 short exact sequence
\[0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0\]이 주어졌다 하자. $A$와 $C$의 projective resolution들 $P_\bullet$, $R_\bullet$이 주어졌다 하면 §분해, ⁋보조정리 7을 이용하여 projective resolution $Q_\bullet \rightarrow B$를 얻는다. 한편, 각각의 $n$에 대해 $R_n$이 projective이므로
\[0 \rightarrow P_n \rightarrow Q_n \rightarrow R_n \rightarrow 0\]은 split exact이다. 이로부터
\[0 \rightarrow F(P_\bullet) \rightarrow F(Q_\bullet) \rightarrow F(R_\bullet) \rightarrow 0\]또한 short exact sequence이며 ([다중선형대수학] §Hom과 텐서곱, ⁋명제 1, 여기에서 homology sequence를 생각하면 원하는 connecting map들과, left derived functor들의 long exact sequence
\[\cdots\overset{\partial}{\longrightarrow}L_iF(A')\longrightarrow L_iF(A)\longrightarrow L_iF(A'')\overset{\partial}{\longrightarrow}L_{i-1}F(A')\longrightarrow L_{i-1}F(A)\longrightarrow L_iF(A'')\overset{\partial}{\longrightarrow}\cdots\]를 얻는다. 이렇게 얻어진 정보가 정의 1의 두 번째 조건을 만족한다는 것은 §분해, ⁋정리 6을 사용하면 된다.
뿐만 아니라, 이들은 정의 3의 센스에서 universal homological $\delta$-functor를 정의한다. 이에 대한 증명은 생략하였다.
명제 8 Enough projective를 갖는 abelian category $\mathcal{A}$와, 임의의 right exact functor $F: \mathcal{A}\rightarrow \mathcal{B}$를 생각하자. 그럼 derived functor들 $L_nF$는 universal $\delta$-functor들이다.

댓글남기기