K

Grad. student in mathematics

앞서 §대수다양체에서 살펴본 것처럼, 우리는 위상공간 위에 정의된 함수들을 다루는 방법을 알아본다.

준층

정의 1 위상공간 $X$가 주어졌다 하자. 그럼 이 위에 정의된 presheaf준층 $\mathcal{F}$는 다음과 같은 데이터로 이루어진다.

  • 각각의 열린집합 $U\subseteq X$마다, 집합 $\mathcal{F}(U)$가 대응된다.
  • 포함관계에 있는 두 열린집합 $U\subseteq V$마다 집합 사이의 함수 $\rho_{VU}:\mathcal{F}(V)\rightarrow\mathcal{F}(U)$가 대응된다.

이들은 다음 조건을 만족해야 한다.

  1. 임의의 열린집합 $U\subseteq X$에 대하여, $\rho_{UU}:\mathcal{F}(U)\rightarrow\mathcal{F}(U)$는 항등함수 $\operatorname{id}_{\mathcal{F}(U)}$이다.
  2. 포함관계에 있는 세 열린집합 $U\subseteq V\subseteq W$에 대하여, $\rho_{WU}=\rho_{VU}\circ\rho_{WV}$이 성립한다.

이 때, $\mathcal{F}(U)$의 원소들을 $U$ 위에서의 section이라 부르고, $\rho$들을 restriction map이라 부른다.

위상공간 $(X,\mathcal{T})$가 주어졌다 하자. 카테고리 $\Top(X)$를

  • $\obj(\Top(X))=\mathcal{T}$,

  • 임의의 $U,V\in\obj(\Top(X))$에 대하여

    \[\Mor_{\Top(X)}(U,V)=\begin{cases}U\hookrightarrow V&\text{if $U\subseteq V$,}\\\emptyset&\text{otherwise.}\end{cases}\]

으로 정의한다. 그럼 $X$ 위에 presheaf를 정의하는 것은 정확하게 contravariant functor $\mathcal{F}:\Top(X)^\op\rightarrow\Set$을 생각하는 것과 같다. 따라서 위의 정의 1에서, $\mathcal{F}(U)$를 집합이 아닌 abelian group이나 ring 등으로 바꿀 경우, $\mathcal{F}$를 $\Top(X)$에서 $\Ab$, $\Ring$으로의 contravariant functor로 취급할 수 있다. 우선은 이러한 차이에 관심을 두지 않지만, 대부분의 경우 우리는 $\mathcal{F}(U)$가 abelian group인 경우를 생각하게 될 것이다.

예시 2 위상공간 $X$가 주어졌다 하고, $\mathcal{F}$를 다음과 같이 정의하자.

  • 임의의 열린집합 $U$에 대하여, $\mathcal{F}(U)$는 $U$에서 $\mathbb{R}$로 가는 연속함수들의 모임이다.
  • 열린집합 $U\subseteq V$가 주어졌을 때, $\rho_{VU}:\mathcal{F}(V) \rightarrow \mathcal{F}(U)$는 $V$에서 정의된 연속함수를 $U$로 제한하는 restriction map이다.

그럼 $\mathcal{F}$는 presheaf가 된다. 이 예시는 $\mathbb{R}$을 임의의 위상공간 $Y$로 바꾸어도 성립하고, 혹은 $X$를 manifold로, $\mathcal{F}$를 $C^\infty$ 함수들의 presheaf로 바꾸는 등의 여러가지 변형을 줘도 성립한다.

Presheaf를 다룰 때에는 항상 위의 예시를 기억하는 것이 도움이 되며, 이러한 관점에서 $U\subseteq V$와, $f\in \mathcal{F}(V)$에 대하여, $\rho_{UV}(f)\in \mathcal{F}(U)$를 간단히 $f\vert_U$로 표기한다.

한편, $\mathcal{F}(U)$들의 모임은 directed system을 이룬다. ([집합론], §극한, ⁋정의 12) 이를 확인하기 위해, $\mathcal{T}$ 위에 순서관계 $\leq$를

\[V\leq U\iff U\subseteq V\]

으로 정의하자.1 그럼 임의의 $U,V\in\mathcal{T}$에 대하여, $U,V\leq U\cap V$이므로 $(\mathcal{T},\leq)$는 right directed set이다. 또, 정의 1에서 restriction map들에 대한 두 조건은 정확히 다음 데이터

\[\bigl((\mathcal{F}(U))_{U\in\mathcal{T}},(\rho_{VU})_{V\leq U}\bigr)\]

가 directed system임을 보여준다. 따라서 이 directed system의 direct limit ([집합론], §극한, ⁋정의 13)이 잘 정의된다.

정의 3 위상공간 $X$ 위에서 정의된 presheaf $\mathcal{F}$를 생각하자. 임의의 점 $p\in X$에 대하여, 점 $p$에서의 stalk줄기 $\mathcal{F}_p$를

\[\mathcal{F}_p=\varinjlim_{p\in U}\mathcal{F}(U)\]

으로 정의한다. $\mathcal{F}_p$의 원소들을 점 $p$에서의 germ싹이라 부른다.

[집합론], §극한, ⁋정의 13 이후에 소개한 $\varinjlim\mathcal{F}(U)$의 construction을 생각하면,

\[\mathcal{F}_p=\{(f,U):p\in U\in\mathcal{T},f\in\mathcal{F}(U)\}/\mathnormal{\sim}\]

임을 알 수 있다. 여기서 $\sim$은

\[(f,U)\sim(g,V)\iff\text{$\exists$ open neighborhood $W\subseteq U\cap V$ of $p$ satisfying $\rho_{UW}(f)=\rho_{VW}(g)$}\]

을 통해 정의되는 동치관계이다. 특별히 예시 2와 같이 $X$를 manifold로 주고, $\mathcal{F}$가 differentiable function들의 presheaf라 생각하면 $\mathcal{F}_p$는 우리가 흔히 알고 있는 differentiable function의 germ들의 모임으로 생각할 수 있다. 그럼 $\mathcal{F}_p$의 원소들은 점 $p$의 무한히 작은 근방에서 일어나는 일을 알고있는 대상들이다.

정의 4 위상공간 $(X,\mathcal{T})$가 주어졌다 하고, 이 위에 두 presheaf $\mathcal{F},\mathcal{G}$가 주어졌다 하자. 그럼 $\mathcal{F}$에서 $\mathcal{G}$로의 presheaf morphism준층 사상 $\phi:\mathcal{F}\rightarrow\mathcal{G}$는 $U\hookrightarrow V$일 때마다 다음 diagram

presheaf_morphism

을 commute하도록 하는 함수들의 모임 $(\phi(U))_{U\in\mathcal{T}}$이다.

우리에게 직관을 주는 예시 2를 생각해보면, 열린집합 $U$에 대하여 정의된 $\phi(U):\mathcal{F}(U) \rightarrow \mathcal{G}(U)$는 $\phi:\mathcal{F}\rightarrow \mathcal{G}$를 열린집합 $U$로 제한하여 얻어지는 함수라 생각할 수 있으므로, 이를 종종 $\phi(U)$ 대신 $\phi\vert_U$로 적는다.

고정된 위상공간 $X$에 대하여, 그 위에서 정의된 presheaf들 $\Top(X)^\op \rightarrow \mathcal{C}$과 presheaf morphism들은 category를 이루며, 이를 $\PSh^\mathcal{C}(X)$로 적는다. Presheaf $\mathcal{F}$를 $\Top(X)$에서 $\mathcal{C}$으로의 contravariant functor로 본다면, presheaf morphism은 별다른 것이 아니라 두 functor $\mathcal{F},\mathcal{G}$ 사이의 natural transformation에 불과하고, 이 관점에서 $\PSh^\mathcal{C}(X)$는 functor category가 된다.

한편, presheaf를 direct system

\[\bigl((\mathcal{F}(U))_{U\in\mathcal{T}},(\rho_{VU})_{V\leq U}\bigr)\]

으로 생각한다면, 위의 정의 4은 presheaf morphism이 directed system 사이의 함수라는 의미가 된다. [집합론], §극한에서는 direct limit에 대한 정리를 거의 소개하지 않았지만, [집합론], §극한, ⁋정의 7과 [집합론], §극한, ⁋명제 8을 direct system에 맞도록 적절히 변형하면 다음 명제를 얻는다.

명제 5 위상공간 $X$ 위에 정의된 presheaf들 사이의 morphism $\phi:\mathcal{F}\rightarrow\mathcal{G}$가 주어졌다 하자. 그럼 임의의 $p\in X$에 대하여, stalk들 사이의 함수 $\phi_p:\mathcal{F}_p\rightarrow\mathcal{G}_p$가 자연스럽게 유도된다.

Abelian presheaf

지금까지 우리는 presheaf가 어떤 카테고리에서 값을 갖는지를 무시해왔는데, 이제 우리는 특별히 카테고리 $\Ab$에서 값을 갖는 presheaf들을 살펴본다. 카테고리 $\mathbf{Ab}$는 특히 diagram chasing을 할 수 있다는 점에서, 즉 abelian category라는 점에서 특별하다. ([범주론] §아벨 카테고리, ⁋정의 7)

정의 6 위상공간 $X$에 대하여, contravariant functor $\Top(X)^\op\rightarrow\Ab$을 abelian presheaf라 부른다.

정의 7 위상공간 $X$ 위에 정의된 abelian presheaf들 사이의 morphism $\phi:\mathcal{F}\rightarrow\mathcal{G}$가 주어졌다 하자. 그럼 $\phi$의 presheaf kernel핵 준층 $\ker\phi$는

  • 각각의 열린집합 $U\subseteq X$마다, $U\mapsto \ker(\phi(U))$

  • 포함관계에 있는 두 열린집합 $U\subseteq V$마다 다음의 diagram

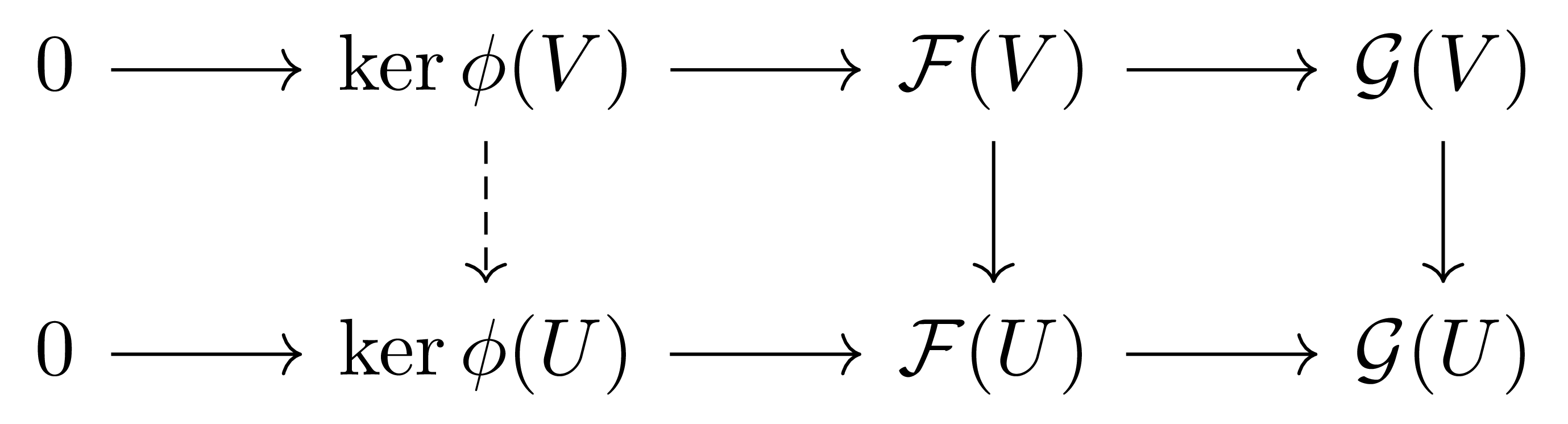
    presheaf_kernel-1

    을 통해 유일하게 결정되는 restriction map $\rho_{VU}:\ker(\phi(V))\rightarrow\ker(\phi(U))$

으로 이루어진 데이터이다.

이 정의에서, $\rho_{VU}$는 $\ker(\phi(U))$의 universal property로부터 유일하게 결정되는 restriction map이다.

보조정리 7 위에서 정의한 $\ker\phi$는 $X$ 위에서의 (abelian) presheaf이다.

증명

다음의 diagram

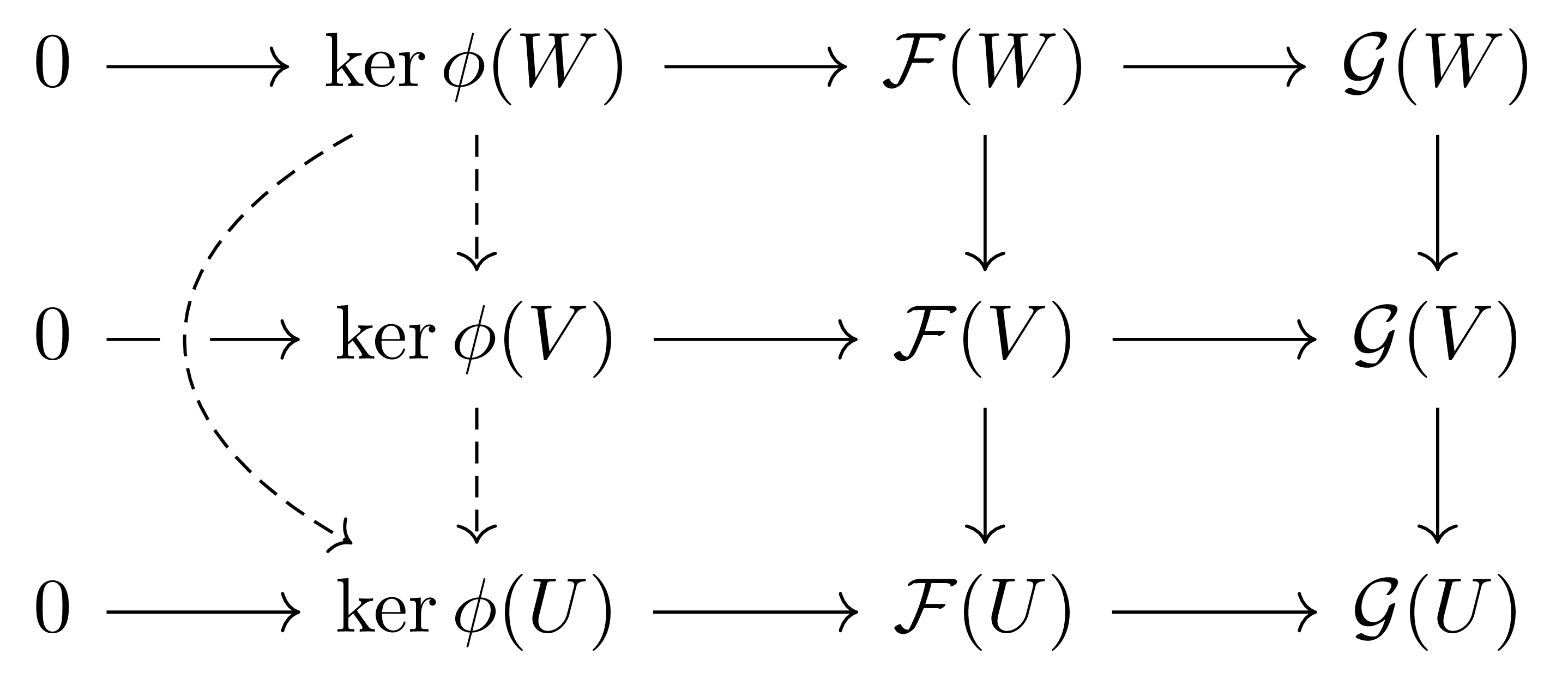
presheaf_kernel-2

와 kernel의 universal property에 의해 자명하다.

이와 마찬가지 방법으로, presheaf cokernel, presheaf image, presheaf coimage 혹은 presheaf quotient 등등을 모두 정의할 수 있다. 두 presheaf $\mathcal{F},\mathcal{G}$의 coproduct $\mathcal{F}\oplus\mathcal{G}$는 $U\mapsto \mathcal{F}(U)\oplus\mathcal{G}(U)$으로 정의된다. 따라서 주어진 위상공간 $X$ 위에서 정의된 abelian presheaf들의 카테고리 $\PSh^\Ab(X)$은 abelian category가 된다.

참고문헌

[Har] R. Hartshorne, Algebraic geometry. Graduate texts in mathematics. Springer, 1977.
[Vak] R. Vakil, The rising sea: Foundation of algebraic geometry. Available online.

  1. Functor $\mathcal{F}$가 contravariant이기 때문에, 어디에선가는 포함관계를 반대로 뒤집어주어야 한다. ↩

댓글남기기