본격적으로 이야기를 시작하기 전에, 우리는 scheme을 정의해야 할 당위성에 대해 먼저 설명한다. 이를 위해서는 scheme이라는 개념이 등장하기 전에 대수기하학에서 어떠한 것들을 공부했고, 어떤 한계가 있었는지를 간략하게 살펴보아야 한다.
고전적인 대수기하학
대수기하에서 생각하는 공간들은 대략적으로 다항식의 해집합으로 나타나는 공간들이고, 대충 이야기하면 이런 공간들을 대수다양체라 부른다. 가령 유클리드 공간 $\mathbb{R}^2$에서 방정식 $y=x^2$이 나타내는 해집합은 포물선이 될텐데, 이러한 해집합들의 성질을 대수적인 방식으로 살펴보는 것이 우리의 목적이라 할 수 있다. 표기의 편의를 위해, 다항함수 $f$에 대하여 $f$의 해집합을 $V(f)$라 하자. 그럼 위에서 정의한 포물선의 경우는 $V(y-x^2)$이라 적을 수 있다.
더 일반적으로, 임의의 field $k$와, 이를 사용해 만든 $n$차원 공간 $k^n$을 생각하자. 그럼 $n$변수 다항함수들의 집합 $I$에 대하여, $V(I)$를 다음 식
\[V(I)=\{(x_1,\ldots, x_n): f(x_1,\ldots, x_n)=0\text{ for all $f\in I$}\}\]으로 정의한다. 즉 $V(I)$는
이다.
예시 1 $\mathbb{R}^2$에서, $V(x,y)$는 두 직선 $x=0$과 $y=0$의 교집합이므로 원점 $(0,0)$을 의미한다. 마찬가지로 $V(y-x^2, y)$를 생각하면, 이는 포물선 $y=x^2$과 직선 $y=0$의 교집합이므로 원점 $(0,0)$을 의미한다.
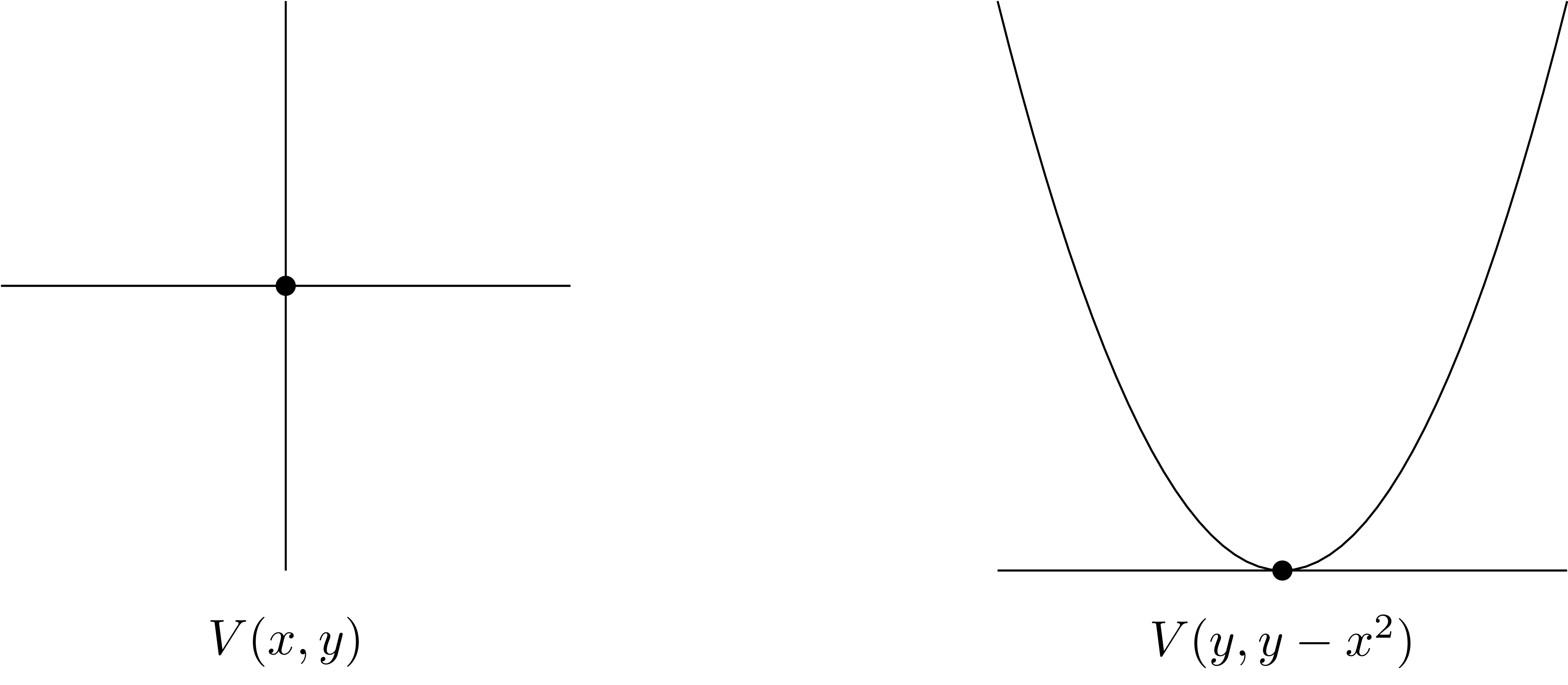
위의 그림에서 첫 번째 경우와 두 번째 경우 사이에는 multiplicity로부터 오는 차이가 있지만, 단순히 $V(I)$만 생각해서는 이 둘을 구별할 수 없다.
예시 1의 두 상황을 구별하기 위해 우리는 공간을 생각할 때, 공간 뿐만 아니라 그 위에 정의된 함수들도 같이 생각하게 된다. 예를 들어 $k^n$을 생각할 때 우리는 이 위에 정의된 다항함수들의 모임, 즉 polynomial ring $k[x_1,\ldots, x_n]$을 함께 생각한다. 이렇게 다항함수들의 모임을 생각했을 때 좋은 점은 $V(I)$ 위에 정의된 함수들의 모임이 이 다항함수들의 모임으로부터 자연스럽게 얻어진다는 것이다.
가령 위의 예시에서 $V(y-x^2)$을 생각해보면, 이 집합 위에서는 두 함수 $g_1(x,y)=x$와 $g_2(x,y)=x-x^2+y$는 같은 함수이다. 어차피 $V(y-x^2)$ 위에서는 $y-x^2=0$이므로 이 두 함수를 구별할 수 없기 때문이다. 즉 $V(y-x^2)$에 정의된 함수들은 다음 ring $\mathbb{R}[x,y]/(y-x^2)$의 원소로 생각할 수 있다. 이를 $V(y-x^2)$의 coordinate ring이라 부르며, 같은 방식으로 임의의 집합 $I$에 대하여 $V(I)$의 coordinate ring를 정의할 수 있다.
예시 2 예시 1에서의 두 집합 $V(x,y)$와 $V(y-x^2,y)$를 생각해보면, $V(x,y)$의 coordinate ring은
\[\mathbb{R}[x,y]/(x,y)\cong \mathbb{R}[x]/(x)\cong\mathbb{R}\]과 같다. 한편 $V(y-x^2,y)$의 coordinate ring은
\[\mathbb{R}[x,y]/(y-x^2,y)\cong\mathbb{R}[x]/(x^2)\]와 같다. 이 두 ring 사이에는 큰 차이가 있는데, 첫 번째 ring에는 $\alpha^2=0$을 만족하는 $\alpha\neq 0$이 존재하지 않지만, 두 번째 ring에서는 $x$가 그러한 원소가 된다는 것이다. 즉 이 상황에서 ring의 nilpotent인 원소가 중근에 해당하는 개념을 나타내고 있는 것을 확인할 수 있다.
이렇게 정의를 하면 약간 미묘한 부분이 있다.
예시 3 $\mathbb{R}^2$에서 정의된 원 $V(x^2+y^2-1)$을 생각하자. 그럼 이 집합 위에서 정의된 두 함수
\[g_1(x,y)=\frac{x^2}{1-y},\quad g_2(x,y)=1+y\]는 본질적으로는 같은 함수여야 한다. 물론 $g_1$은 점 $(0,1)$에서 정의가 되지 않는 함수이긴 하지만, 그 점만 제외하면 식
\[\frac{x^2}{1-y}=1+y\]이 $V(x^2+y^2-1)$에서 항상 성립하며, 뿐만 아니라 $(0,1)$에서의 값을 적당히 잘 정의해서 $g_1$을 확장할 수도 있으므로 이 경우에는 $g_1$의 정의역은 사실 그렇게 큰 문제가 되지 않는다.
이런 차원에서 우리는 $V$ 위에 정의된 함수들의 모임을 생각할 때 regular function들을 생각하게 되고, 이는 각각의 $p\in V$마다 적당한 근방 $U\subseteq V$가 존재하여 여기에서는 $g/h$ 꼴로 쓸 수 있는 함수들을 말한다. (물론, $g,h$는 다항식이고 $h$는 $U$에서는 $0$이 되지 않는다.)
스킴
남은 글에서는 우리가 scheme에게 기대하는 성질과, 이를 대략적으로 어떻게 정의할지를 이야기한다.
우선 scheme은 단순한 위상공간이 아니다. 예시 2에서 우리가 위상적으로는 똑같아보이는
Scheme을 정의하기 위한 우리의 여로는 대강 다음과 같다.
- 우선,
위상공간 위에 정의된 함수들의 정보 라는 말을 잘 설명할 필요가 있다. 가령 복소해석학에서의 Liouville theorem을 생각해보면 $\mathbb{C}$ 위에서 정의되고, bounded인 함수는 상수함수 뿐이므로 $\mathbb{P}^1$ 위에서 정의되는 함수는 상수함수 뿐이어야 한다. 우리는 당연히 이러한 상황을 원하지 않으므로 $\mathbb{P}^1$ 전체에서 정의된 함수 대신,모든 열린집합마다 그 위에 국소적으로 정의된 함수들의 모임을 생각하게 된다.
이를 위해 우리는 §준층과 §층에서 presheaf와 sheaf라는 개념을 정의하게 된다. 직관적으로 presheaf는 그냥 열린집합마다 함수들을 모아놓은 것이고, sheaf는 어떠한 종류의 gluing이 가능한 presheaf라고 생각하면 된다. - 그 후, 임의의 (commutative) ring $A$로부터 특정한 위상공간 $\Spec A$과 그 위에 정의된 함수들의 sheaf $\mathscr{O}_{\Spec A}$를 만들어내는 과정을 §스펙트럼에서 다룬다. 이 단계에서 ring homomorphism이 ringed space 사이의 morphism을 유도하고, 따라서 $\Spec$이 $\cRing$에서 ringed space로의 contravariant functor임을 살펴본다.
- §환 달린 공간에서는 우선 locally ringed space와 이들 사이의 morphism을 정의한다. Locally ringed space들의 category는 ringed space들의 category의 full subcategory는 아니지만, 이것이 옳은 category이다. 그 이유는 $\Spec$의 essential image가 locally ringed space들의 category의 full subcategory가 되기 때문이다. 이러한 꼴의 locally ringed space들을 affine scheme이라 부른다.
- 마지막으로 §스킴에서 우리는 드디어 scheme이 무엇인지 정의한다. Manifold가 국소적으로 유클리드 공간과 닮아있는 위상공간이듯, scheme은 국소적으로 affine scheme과 닮아있는 locally ringed space이다.
Scheme을 다룰 때 우리가 하는 일은 다른 기하학에서 하는 것과 크게 다르지 않다. 즉 다른 기하학에서 chart를 잡아서 여러가지 정의나 계산을 하는 것처럼, scheme에서도 affine scheme들을 잡아서 정의나 계산을 하게 된다. 차이점이 있다면, affine scheme은 철저하게 대수적으로 볼 수 있는 대상이라는 것이다. 이는 위의 3번 단계에서 우리가 한 것이, 본질적으로는 affine scheme을 $\cRing^\op$이라고 정의한 것이기 때문이다.
이렇게 앞으로 나올 몇 개의 글에서 scheme이 무엇인지를 잘 잡아낸다면 그 이후의 글들에서는 크게 어려움이 없을 것이다.

댓글남기기