Abelian group에서와는 다르게, 앞선 글에서 정의한 weak direct product는 일반적인 group에서 universal property를 만족하지 않는다.
예시 1 임의의 nonabelian group $G$를 생각하고, $a,b\in G$에 대해 $ab\neq ba$가 성립한다 하자. Group homomorphism $f_1, f_2: (\mathbb{Z},+)\rightarrow (G,\cdot)$을
\[f_1(1)=a, \qquad f_2(1)=b\]을 통해 정의하자. Index set $I=\{1,2\}$가 유한집합이므로 $(\mathbb{Z},+)$ 두 개의 weak direct product는 $\mathbb{Z}\times\mathbb{Z}$와 같다.
그러나 우리는 다음의 diagram
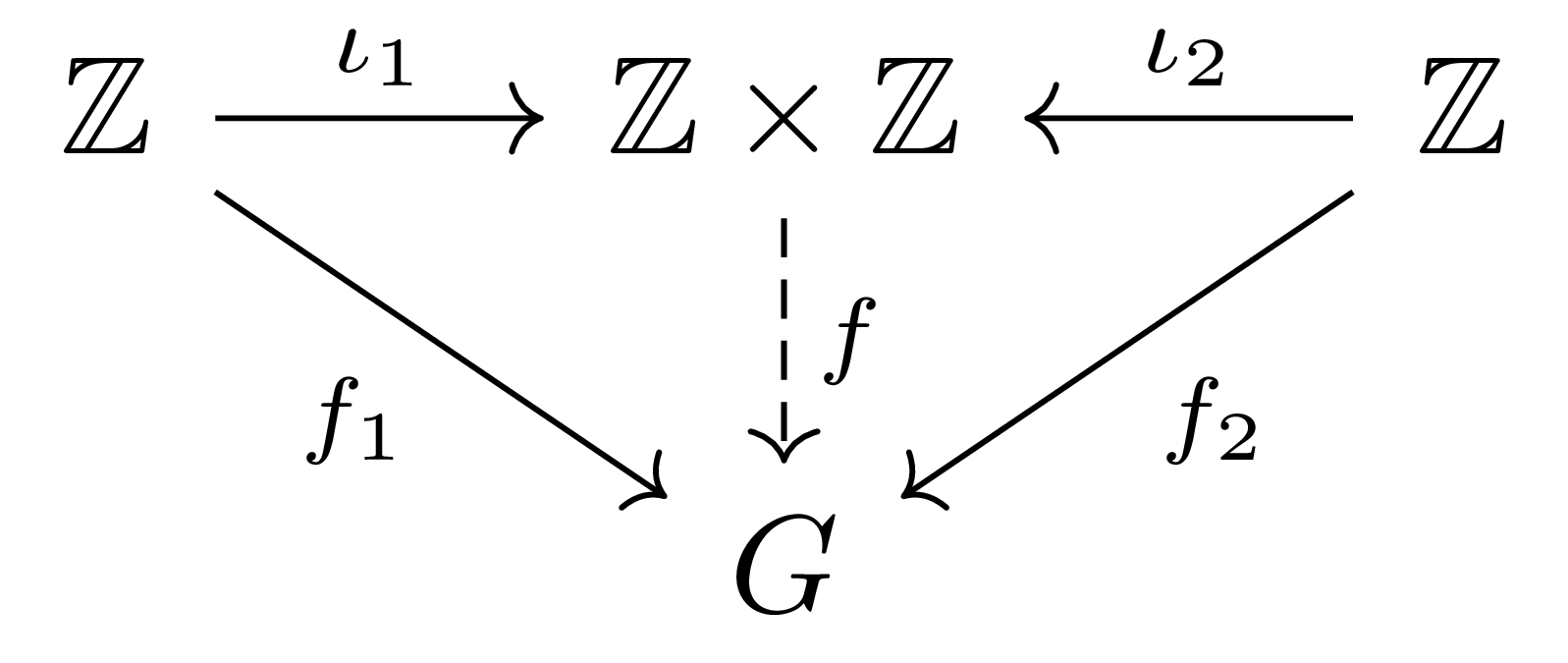
을 commute하게 만드는 $f:\mathbb{Z}\times\mathbb{Z}\rightarrow G$는 존재하지 않음을 알 수 있다. 만일 그러한 $f$가 존재한다면
\[\begin{aligned}ab&=f_1(1)f_2(1)=f(\iota_1(1))f(\iota_2(1))=f(\iota_1(1)+\iota_2(1))\\ &=f(\iota_2(1)+\iota_1(1))=f(\iota_2(1))f(\iota_1(1))=f_2(1)f_1(1)\\ &=ba\end{aligned}\]가 되어 $a,b$의 선택에 모순이기 때문이다.
그러므로 일반적인 group들 사이에서 direct sum과 같이, universal property를 만족하는 대상을 찾기 위해서는 새로운 방법을 도입해야 한다.
Free group
우선 다음 정의를 먼저 살펴보자.
정의 2 공집합이 아닌 집합 $X$에 대하여, $X$에 의해 정의된 free group은 다음과 같은 universal mapping problem의 solution $(F,\iota)$으로 정해진다.
임의의 group $G$에 대하여, 만일 어떤 함수 $f:X\rightarrow G$가 주어졌다면 유일한 group homomorphism $\bar{f}:F\rightarrow G$가 존재하여 $\bar{f}\circ\iota=f$를 만족한다.
위의 정의를 만족하는 쌍들은 모두 전단사함수에 대해 유일함이 분명하다. 문제는 이러한 pair가 적어도 하나는 존재한다는 것을 보이는 부분이다.
대략적인 흐름을 소개한다. 우선 $X$와 disjoint하며 같은 cardinality를 갖는 집합 $X^{-1}$을 생각하자. $X^{-1}$은 어떤 특별한 집합이 될 이유는 없지만, 우리는 bijection $X\rightarrow X^{-1}$ 하나를 골라 $x\in X$의 $X^{-1}$에서의 image를 $x^{-1}$으로 표기할 것이다. 또, $X\cup X^{-1}$과 disjoint한 한원소집합을 하나 골라 이 집합의 원소를 $e$라 하자.
그럼 group $F$의 원소는 집합 $X\cup X^{-1}\cup \{e\}$에 의해 정의되는 reduced word들의 모임이다. 여기서 word라는 것은 그저 집합 $X\cup X^{-1}\cup \{e\}$의 원소들의 나열인데, 만일 $xx$와 같이 같은 원소가 두 번 연달아 나열되거나, $xx^{-1}$과 같이 $x$ 직후에 $x^{-1}$이 나열되거나, $xey$와 같이 두 개의 항 사이에 $e$가 있을 경우 이들을 각각 $x^2$, $e$, $xy$으로 줄여 쓸 수 있다. 하지만, 예를 들어 $y\neq x^{-1}$이라면 $xyx$를 줄여 쓸 방법은 없다. 이렇게 줄여 쓴 word를 reduced word라 부른다.
우리는 모든 word를 reduced word로 줄여 쓸 수 있다.1 이들 사이의 연산과 항등원을 정의하자. 항등원은 당연히 reduced word $e$이다. 연산은 그냥 두 개의 word를 이어쓴 후, 이를 reduced word로 줄여 쓴 것으로 정의된다. 예를 들어 word $x_1x_2$와 $x_3x_4$의 연산은 $x_1x_2x_3x_4$로 주어진다. 그럼 $e$는 이 연산 하에서의 empty word로 볼 수도 있다. 이 연산은 자명하게 associative하다. 역원은 원래 주어진 원소의 각 항들의 역원 취한 후, 이를 거꾸로 나열한 것이다. 예를 들어 다음의 word
\[x_1x_2^{-1}x_3^2\]의 역원은
\[x_3^{-2}x_2x_1^{-1}\]이 되며, 실제로 이들 둘을 연산해보면 $e$가 됨을 확인할 수 있다.
이제 우리는 group $F$를 만들었으며, 여기서 $X$의 원소로 이루어진 길이 1짜리 원소들을 $X$의 원소와 동일시하면 $\iota:X\rightarrow F$ 또한 얻는다. 그럼 이들이 정의 2의 universal property를 만족한다는 것을 쉽게 보일 수 있다. 이를 위해서는 $\bar{f}$를 $F$에 등장하는 원소들 $x\in X$들을 모두 $g(x)$로 바꿔주는 함수로 정의한 후, 이것이 group homomorphism이 된다는 것을 확인하면 된다.
따름정리 3 임의의 group $G$는 free group의 homomorphic image이다.
증명
$G$의 generator들의 모임 $X$를 생각한 후, $X$에 대한 free group $F$를 생각하자. 함수 $X\hookrightarrow G$에 의해 정의되는 $F$에서 $G$로의 group homomorphism이 존재하며, 이 homomorphism의 image는 $G$의 generator들을 모두 포함하므로 surjective하다.
Free product
위의 아이디어를 응용하면 비슷하게 free product 또한 정의할 수 있으며, 이는 우리가 찾아헤매던 [집합론], §집합의 합, ⁋정리 8와 같은 universal property를 갖는 group이 된다. 마찬가지로 construction은 간략하게만 소개한다.
Group들의 family $(G_i)$가 주어졌다 하자. 편의를 위해 이들이 모두 서로 disjoint하다고 하고, $X=\bigcup G_i$라 하자. 즉, 임의의 원소 $x\in X$에 대하여 $x\in G_i$인 $i$를 유일하게 찾을 수 있다. $G_i$들은 이미 역원을 포함하고 있으므로, generator들의 모임으로는 $X\cup\{e\}$만 생각하면 충분하다.
$(G_i)$들의 free product $\prod^\ast G_i$는 이 집합 $X\cup\{e\}$에서 만들어지는 reduced word들의 모임이다. 큰 흐름은 free group을 정의할 때와 같지만, 이번에는 $G_i$의 원소들이 자신들끼리 연산이 가능하므로 reduced word를 정의할 때 조금 더 신경을 써 주어야 한다. Free product를 정의할 때 사용하는 reduced word라는 말은 집합 $X\cup\{e\}$의 원소들로 만들어진 word
\[x_1x_2\cdots x_n\]가 다음의 세 조건을 만족한다는 것을 의미한다.
- 만일 $n>1$이라면 $x_k$들 가운데 어떤 것도 $e$와 같지 않다.
- 만일 $x_k\in X$라면 $x_k$는 이 원소가 포함된 group $G_i$에서 항등원이 아니다.
- 인접한 두 원소 $x_i, x_{i+1}$은 반드시 서로 다른 group에 속한다.
임의의 word가 주어졌을 때, 이를 reduced word로 만드는 법은 간단하다. 인접한 원소들이 서로 같은 group에 속하는 원소인지를 모두 체크해본 후, 같은 group에 속하는 원소들은 이 group에서의 연산을 통해 하나의 원소로 합쳐준다. 이 과정에서 (혹은 원래부터) 어떤 group에서의 항등원이 나왔다면, 그 원소는 지워버리면 된다.
그럼 $\prod^\ast G_i$ 위의 연산은 free group을 정의할 때와 동일하게
예시 4 예시 1과 동일한 상황을 생각하자. 대신 표기상의 편의를 위해 $G_1=\langle a\rangle\cong\mathbb{Z}$, $G_2=\langle b\rangle\cong\mathbb{Z}$이라 하자. 그럼 $G_1\ast G_2$의 원소는 다음과 같은 원소들
\[ab, a^2b, a^{-1}ba^3, bab^2, \cdots\]의 모임이다. 예를 들어, 두 개의 원소 $a^2b$와 $bab^2$를 연산하면 우리는
\[(a^2b)(bab^2)=a^2bbab^2=a^2b^2ab^2\]을 얻는다.
이 때 $\langle a\rangle$과 $\langle b\rangle$은 $G_1\ast G_2$의 cyclic subgroup이고, 따라서 $G_1$과 $G_2$에서 $G_1\ast G_2$으로의 homomorphism을 $a\mapsto a$, $b\mapsto b$로 정의하면 자연스러운 inclusion map $\iota_1$과 $\iota_2$를 얻는다.
물론 예시 1과 같은 문제 또한 일어나지 않는다. $\iota_1(a)\iota_2(b)=ab$이고 $\iota_2(b)\iota_1(a)=ba$인데, 이 두 원소는 $\prod^\ast G_i$의 서로 다른 원소이기 때문이다.
참고문헌
[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.
-
Word들 사이의 연산을 정의해주기 위해 reduced word를 꼭 도입해줘야 하는 것은 아니지만, 표현의 유일성을 위해 reduced word를 도입해주는 것이 좋다. ↩

댓글남기기