군의 직접곱

직접곱의 정의

대수적 구조에 곱을 정의할 때에는 [집합론] §집합의 곱, ⁋정리 3과 마찬가지 방법으로 universal property를 이용해 정의한다. 어차피 universal property를 만족하는 대상이 존재한다는 것을 보이기 위해서 아래 보조정리 2와 같이 직접 대상을 정의해주어야 하는 것은 마찬가지지만, universal property를 사용하는 정의가 조금 더 본질적이기 때문이다.

정의 1 Group들의 family $(G_i)$가 주어졌다고 하자. 그럼 어떤 group $G$와, group homomorphism들 $\pr_i:G\rightarrow G_i$가 이들 family의 direct product_직접곱라는 것은, 다음의 universal property가 성립하는 것이다.

임의의 group $H$와 group homomorphism들 $f_i:H\rightarrow G_i$들이 주어졌을 때, $f_i=\pr_i\circ f$이도록 하는 유일한 group homomorphism $f:H\rightarrow \prod_{i\in I} G_i $가 존재한다.

이 정의가 말이 되기 위해서는 이러한 성질을 만족하는 $(G,(\pr_i)_{i\in I})$가 적어도 하나 존재해야 한다.

보조정리 2 정의 1의 universal property를 만족하는 $(G,(\pr_i)_{i\in I})$이 존재한다.

증명

우선 주어진 성질을 만족하는 곱집합 $\prod_{i\in I} G_i$는 이미 [집합론] §집합의 곱, ⁋정의 1에서 정의했다. 표기상의 편의를 위해 $\prod_{i\in I}G_i$의 원소 $f:I\rightarrow \bigcup G_i$를 순서쌍 $(a_i)_{i\in I}$으로 표기하기로 한다.

이제 집합 $\prod_{i\in I}G_i$의 임의의 두 원소 $x=(x_i)_{i\in I},y=(y_i)_{i\in I}$에 대하여,

\[xy=(x_i)_{i\in I}(y_i)_{i\in I}=(x_iy_i)_{i\in I}\]

으로 정의하자. 그럼 $\prod_{i\in I}G_i$는 이 연산에 대해 group의 구조를 가지며, 항등원은 $(e_i)_{i\in I}$이고 $x=(x_i)_{i\in I}$의 역원은 $(x_i^{-1})_{i\in I}$인 것을 알 수 있다. 또, 임의의 $j\in I$에 대하여

\[\pr_j(xy)=\pr_j(x_iy_i)_{i\in I}=x_jy_j=\pr_j(x)\pr_j(y)\]

이므로 $\pr_j$가 group homomorphism이다.

이제 이렇게 정의한 $(G=\prod_{i\in I}G_i,(\pr_i)_{i\in I})$가 정의 1의 universal property를 만족하는 것을 증명하자. 이를 위해서는 곱집합의 universal property로 얻어지는 함수 $f:H\rightarrow G$가 group homomorphism이라는 것만 보이면 충분하다. 이제 임의의 $x,y\in H$와 임의의 $i\in I$에 대하여,

\[f(xy)=(f_i(xy))_{i\in I}=(f_i(x)f_i(y))_{i\in I}=(f_i(x))_{i\in I}(f_i(y))_{i\in I}=f(x)f(y)\]

이므로 $f$는 group homomorphism이 되고 따라서 위의 $(G=\prod_{i\in I}G_i,(\pr_i)_{i\in I})$가 universal property를 만족한다.

다음 따름정리들은 정의 1로부터 자명하다.

따름정리 3 Group들의 family $(G_i)$에 대하여, 이들 family의 product는 isomorphism에 대해 유일하다.

증명

정의 1의 universal property를 만족하는 두 $(G,(\pr_i)),(G’,(\pr_i’))$이 존재한다 가정하자. 그럼 $G$의 universal property로부터 다음 diagram을 commute하도록 하는 $\psi$가 유일하게 존재한다.

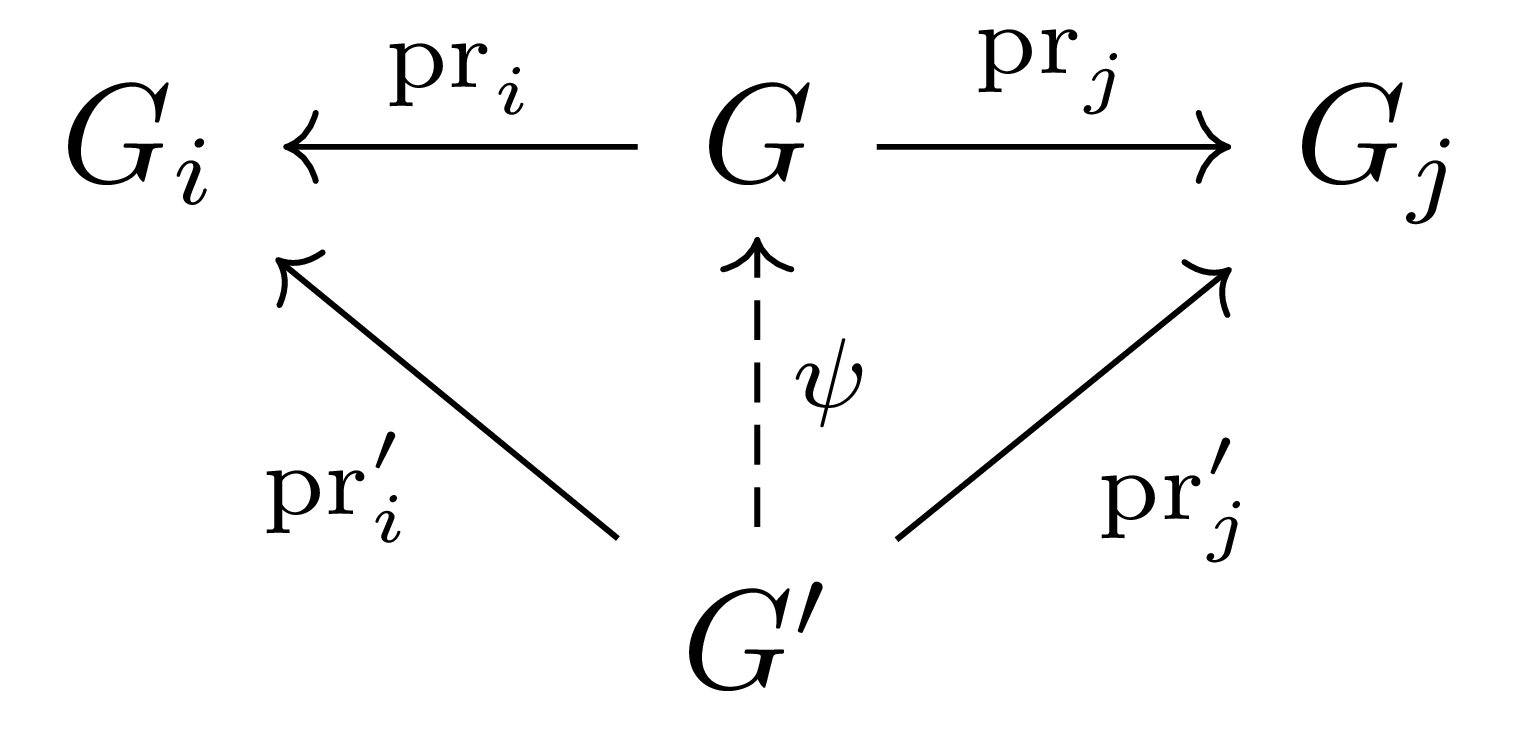
비슷하게 $G’$의 universal property로부터 다음 diagram을 commute하도록 하는 $\phi$가 유일하게 존재한다.

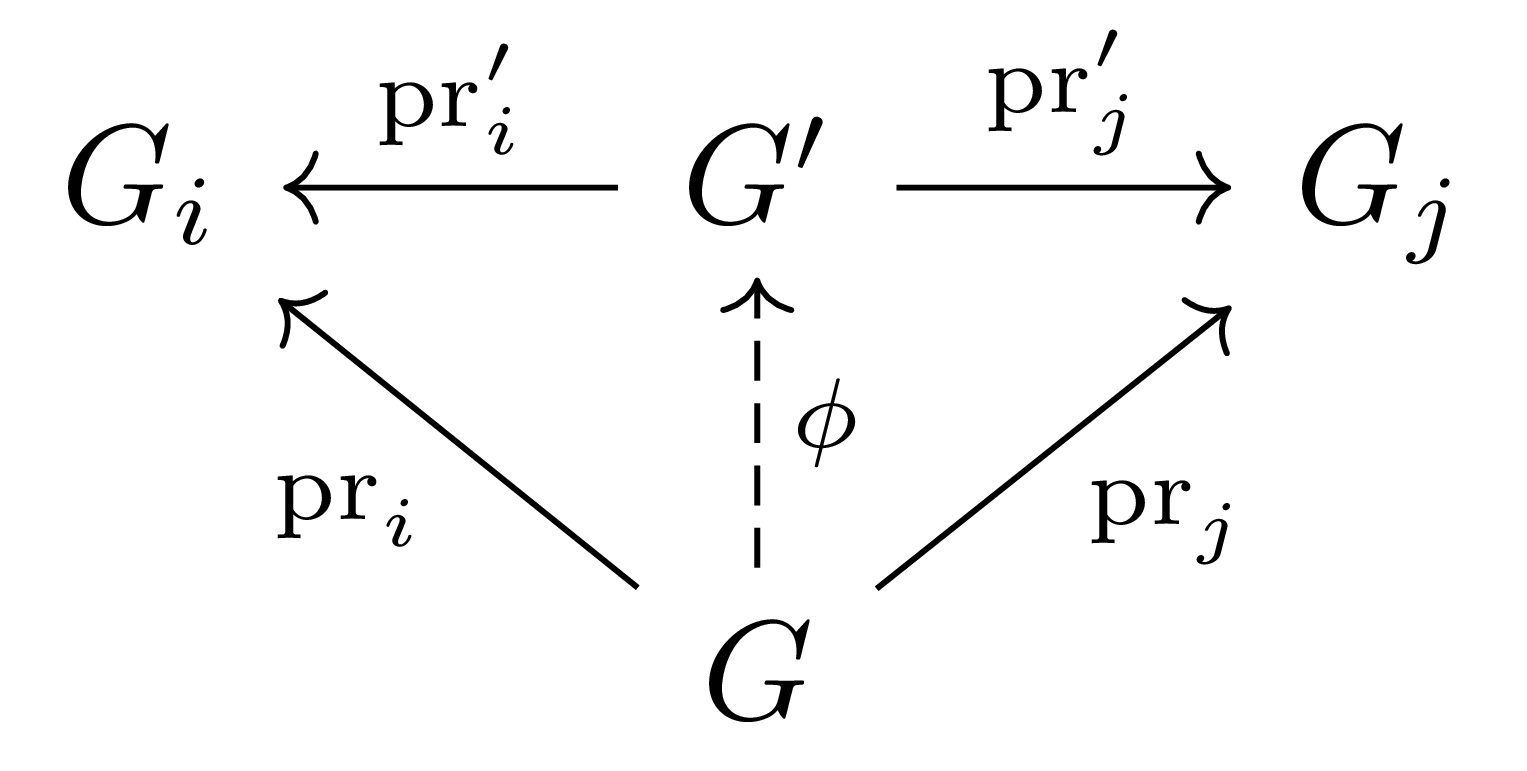
이제 두 group homomorphism $\id_G, \phi\circ\psi$가 모두 다음의 diagram

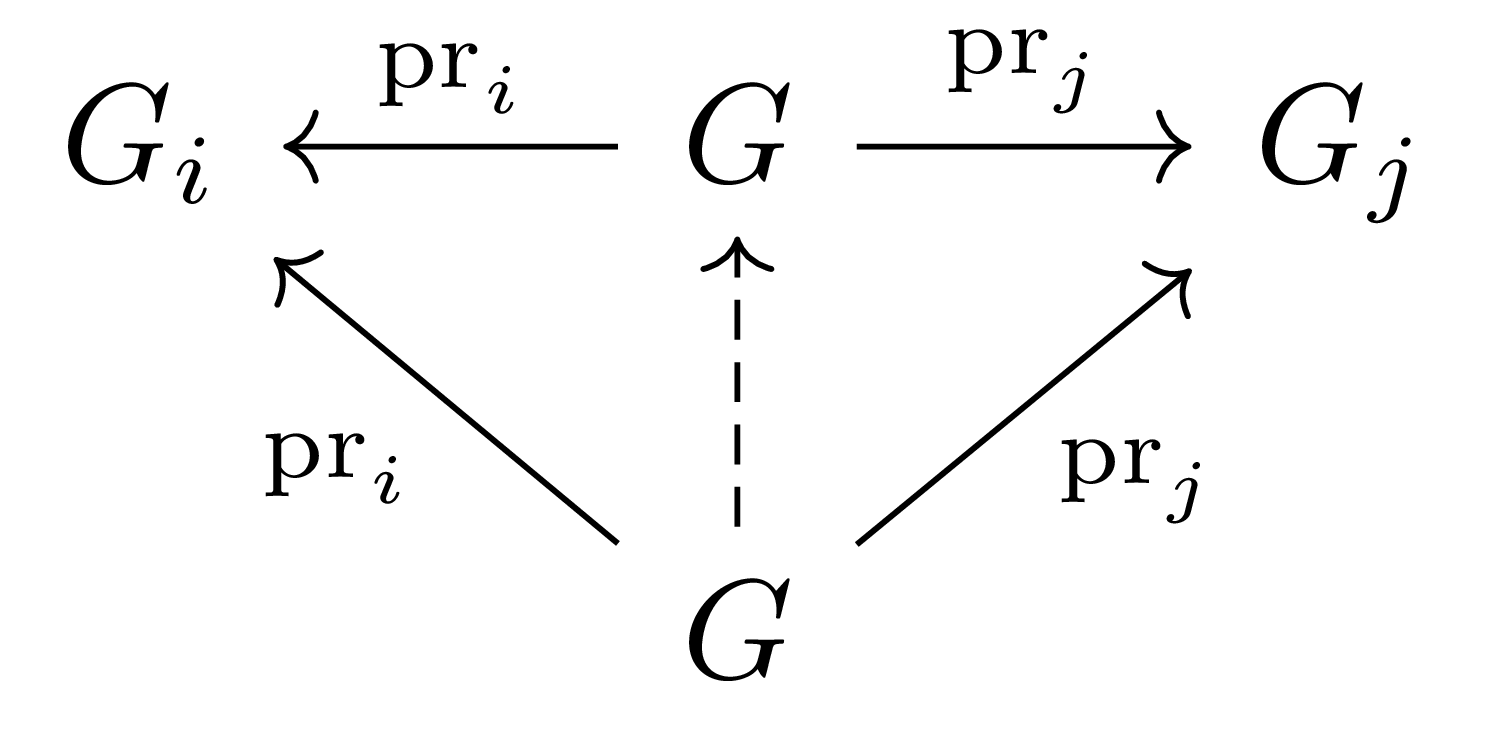
을 commute하도록 하므로, universal property에 의하여 $\id_G=\phi\circ\psi$가 성립한다. 비슷한 논리에 의해 $\id_{G’}=\psi\circ\phi$가 성립하고 따라서 $\phi$와 $\psi$는 isomorphism이다.

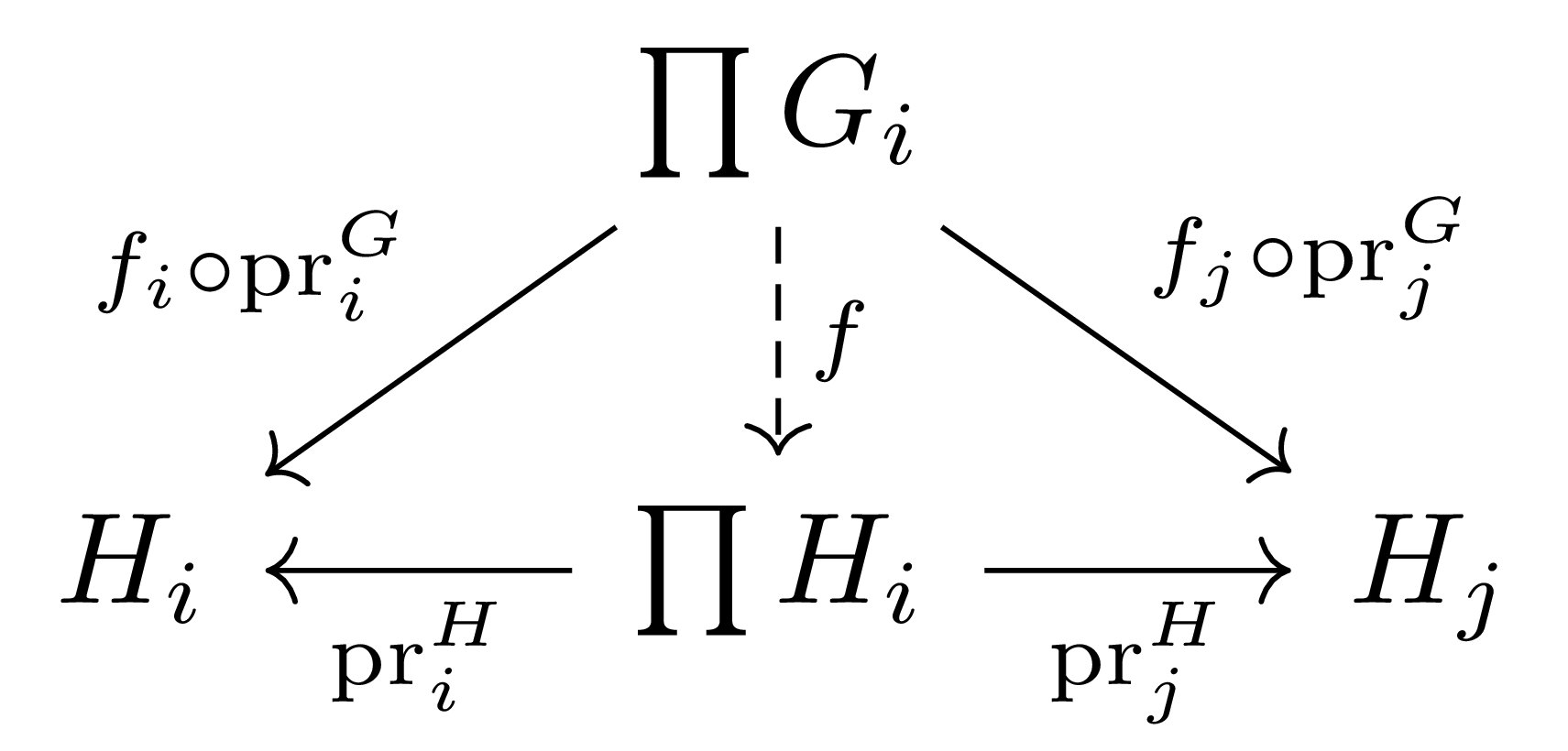
따름정리 4 $(G_i)$, $(H_i)$가 동일한 집합 $I$를 index set으로 갖는 group들의 family이고, 각각의 $i$마다 group homomorphism $f_i:G_i\rightarrow H_i$가 주어졌다 하자. 그럼 다음의 diagram

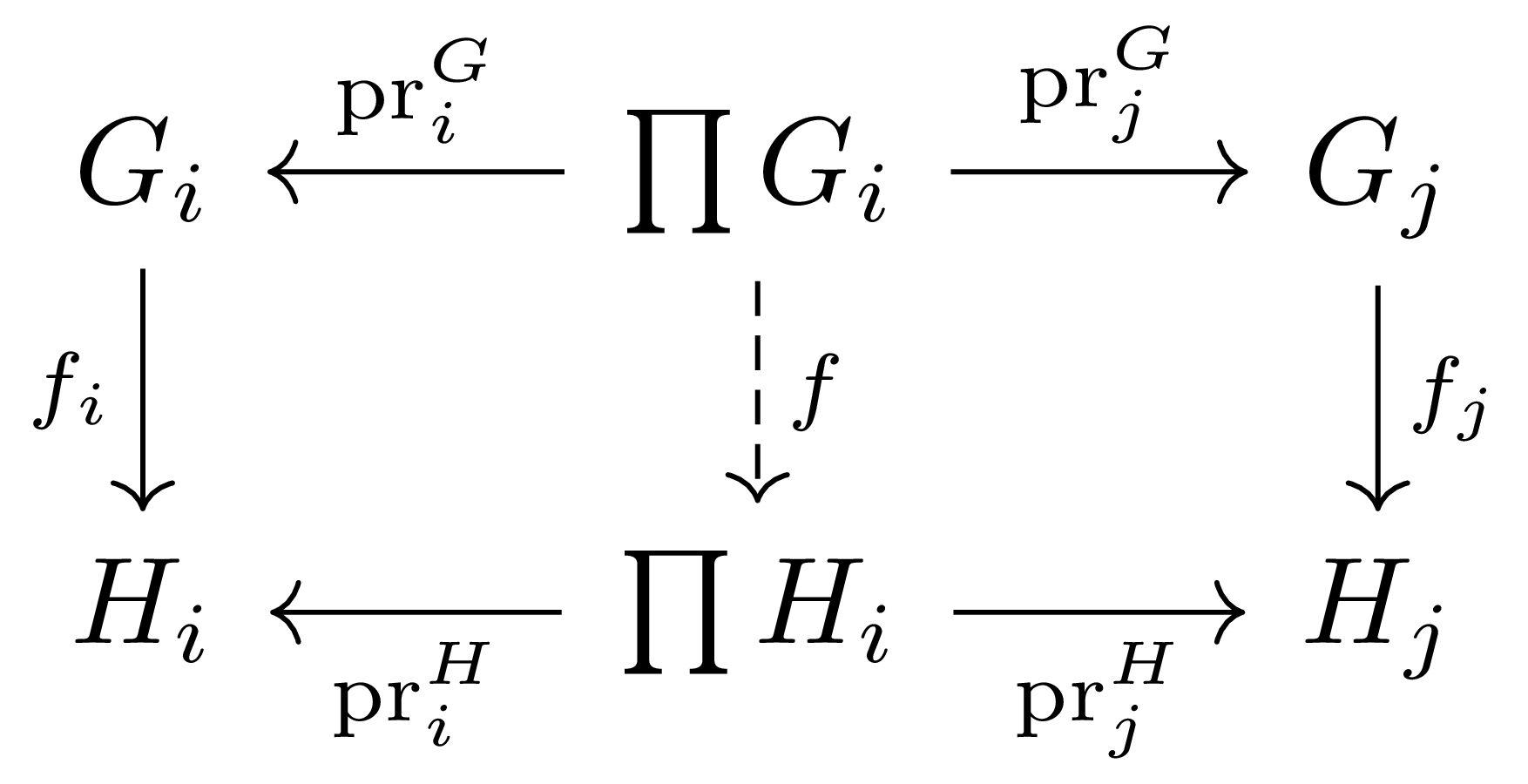
을 commute하도록 하는 유일한 group homomorphism $f:\prod G_i\rightarrow\prod H_i$이 존재한다. 이 때 $\ker f=\prod\ker f_i$이고, $\im f=\prod\im f_i$이다.

증명

$f$를 만들기 위해서는 group homomorphism들 $f_i\circ\pr_i^G$에 $H$의 universal property를 적용하면 된다.

이 때,

\[x\in\ker f\iff f(x)=e\iff \forall i(\pr_i^H(f(x))=e_i)\iff \forall i((f_i\circ \pr_i^G)(x)=e_i)\iff \forall i(\pr_i^G(x)\in\ker f_i)\]

이므로 $\ker f=\prod\ker f_i$가 성립한다.

이와 유사하게, $y\in\prod H_i$에 대해 $y\in\im f$인 것은 $y=f(x)$인 $x\in H_i$가 존재하는 것과 동치이고, 이러한 $x$에 대하여

\[\pr_i^H(y)=\pr_i^H(f(x))=f_i(\pr_i^G(x))\in\im f_i\]

이므로 $\im f=\prod\im f_i$ 또한 성립한다.

따름정리 5 Group들의 family $(G_i)_{i\in I}$가 주어졌다 하자. 각각의 $i\in I$에 대하여 $H_i$들이 $G_i$의 normal subgroup이라면, $\prod H_i$도 $\prod G_i$의 normal subgroup이고 그 quotient group은 $\prod (G_i/H_i)$와 같다.

증명

이번에는 canonical homomorphism들 $p_i:G_i\rightarrow G_i/H_i$들에 따름정리 4를 적용하면 된다.

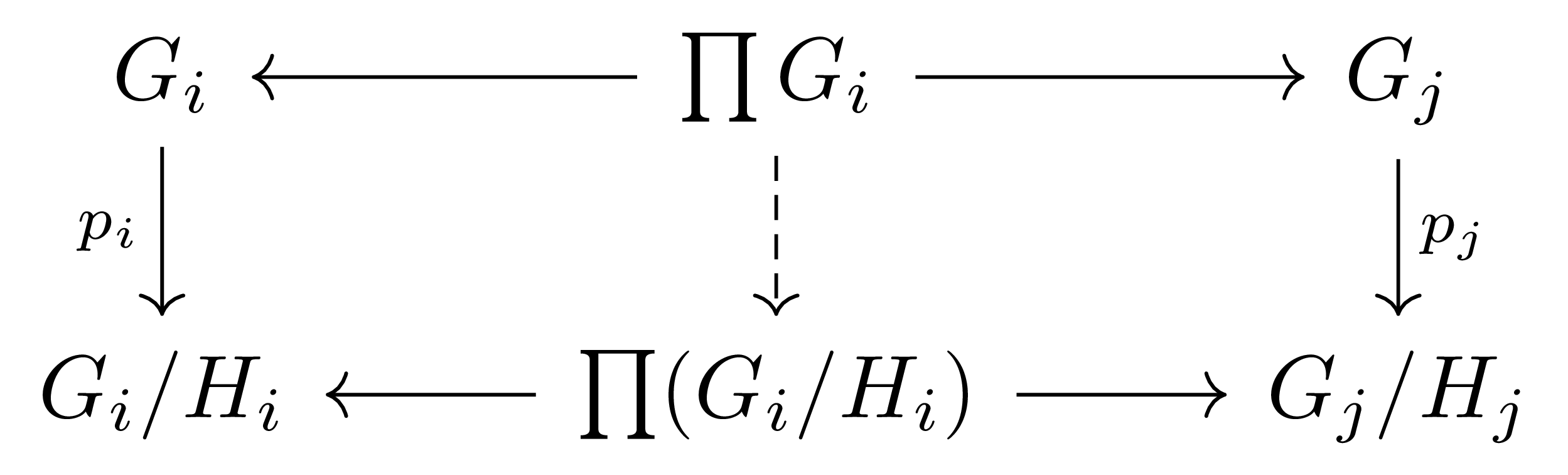
$p_i\circ\pr_i$들 각각은 전사인 homomorphism들의 합성이므로 전사이고 따라서 앞선 따름정리에 의해 $\im p$는 $\prod(G_i/H_i)$와 같다. 또, $p_i$들 각각의 kernel은 $H_i$와 같다. 따라서 first isomorphism theorem에 의하여

\[\biggl(\prod_{i\in I} G_i\biggr)\bigg/\biggl(\prod_{i\in I}H_i\biggr)\cong\prod_{i\in I} (G_i/H_i)\]

가 성립한다.

물론, $H_i$들이 $G_i$들의 normal이 아닌 subgroup이더라도 $\prod H_i$는 $\prod G_i$의 subgroup이 된다.

따름정리 6 Group들의 family $(G_i)_{i\in I}$가 주어졌다 하자. 만일 각각의 $i\in I$에 대하여 $H_i\leq G_i$라면, $\prod H_i$는 $\prod G_i$의 subgroup이다.

증명

Inclusion homomorphism들 $\iota_i:H_i\hookrightarrow G_i$에 따름정리 4를 적용하면, $\iota$는 단사이고 $\prod H_i$는 정확히 $\iota$의 image이므로 $\prod G_i$의 subgroup이다.

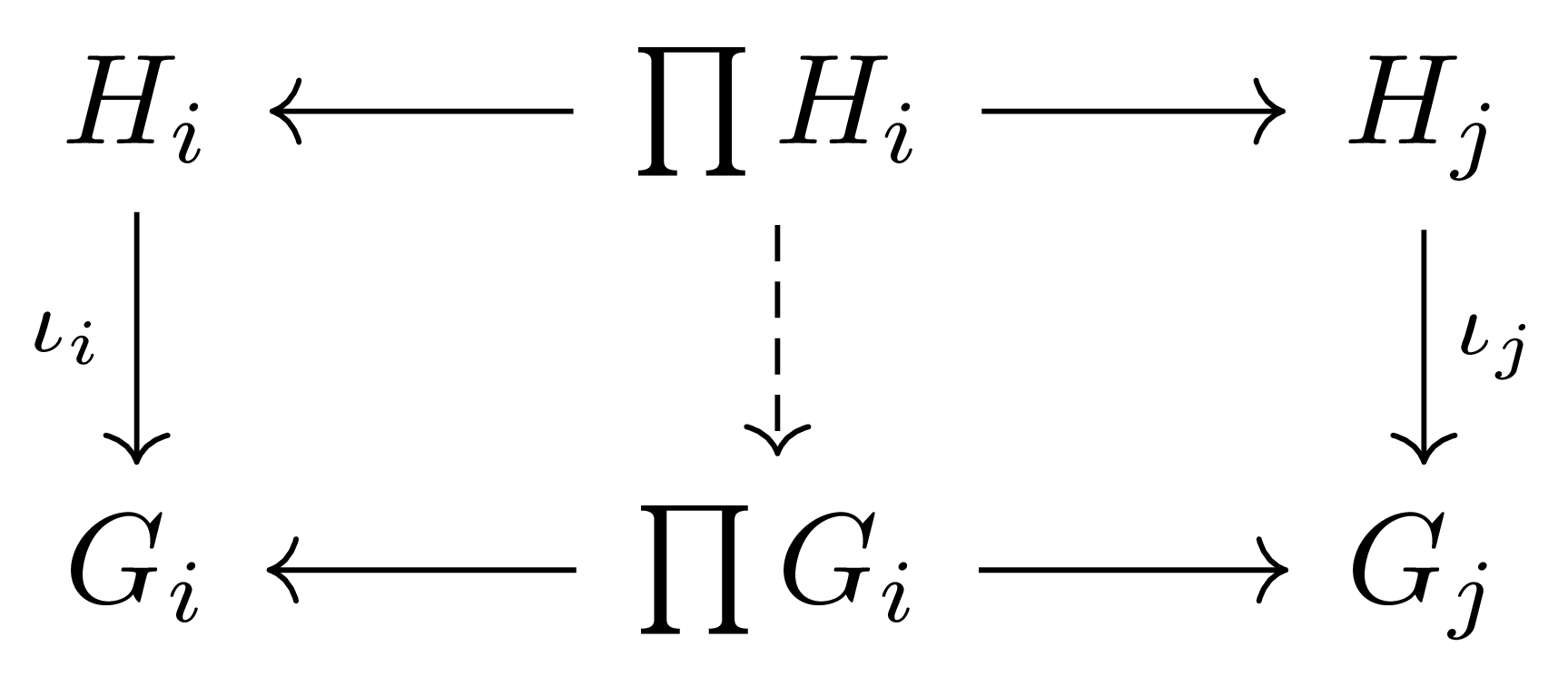
부분곱

위의 따름정리들은 다음의 상황에서 특히 유용하다.

$(G_i)_{i\in I}$가 group들의 family라 하고, $I$의 부분집합 $J$를 생각하자. 그럼 product $\prod_{j\in J}G_j$가 잘 정의된다. 한편, 다음의 식

\[G_i'=\begin{cases} G_i&i\in J\\ \{e\}&i\not\in J\end{cases}\]

으로 정의된 group들의 family $(G_i’)$, 그리고 $G_i’$에서 $G_i$로의 group homomorphism들

\[f_i=\begin{cases} \id_{G_i}&i\in J\\ \iota_i&i\not\in J\end{cases}\]

을 생각하자. 그럼 어렵지 않게 $\prod_{i\in I}G_i’\cong\prod_{j\in J}G_j$임을 보일 수 있으며, 따라서 따름정리 5에 의하여 다음의 식

\[\biggl(\prod_{i\in I}G_i\biggr)\bigg/\biggl(\prod_{j\in J}G_j\biggr)\cong\prod_{i\in I\setminus J} G_i\]

이 성립함을 확인할 수 있다.

---

참고문헌

[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.

---