아이디얼들의 곱
정의 1 Ring $A$의 두 two-sided ideal $\mathfrak{a},\mathfrak{b}$에 대하여, 이들의 곱product $\mathfrak{a}\mathfrak{b}$는 다음 집합
\[\mathfrak{a}\mathfrak{b}=\{x_1y_1+x_2y_2+\cdots+x_ny_n: x_i\in \mathfrak{a}, y_i\in \mathfrak{b}, n\geq 1\}\]을 의미한다.
$\mathfrak{a}\mathfrak{b}$이 $A$의 덧셈에 대한 subgroup임은 자명하다. 한편 $\mathfrak{a}\mathfrak{b}$의 임의의 원소 $x_1y_1+\cdots+x_ny_n$와, $A$의 임의의 원소 $x$에 대하여,
\[x(x_1y_1+\cdots+x_ny_n)=xx_1y_1+\cdots xx_ny_n\]이고 $xx_i\in \mathfrak{a}$이므로 $x(x_1y_1+\cdots+x_ny_n)\in \mathfrak{a}\mathfrak{b}$이다. $x$를 오른쪽에 곱해도 비슷한 논증이 성립하므로, $\mathfrak{a}\mathfrak{b}$는 $A$의 two-sided ideal인 것을 확인할 수 있다.
명제 2 위와 같이 정의된 곱셈에 대하여, $A$의 two-sided ideal들의 모임은 항등원을 $A$로 하는 monoid 구조를 가진다. 뿐만 아니라, 분배법칙
\[\mathfrak{a}(\mathfrak{b}+\mathfrak{c})=\mathfrak{a}\mathfrak{b}+\mathfrak{a}\mathfrak{c},\quad (\mathfrak{a}+\mathfrak{b})\mathfrak{c}=\mathfrak{a}\mathfrak{c}+\mathfrak{b}\mathfrak{c}\]도 성립한다.
증명
세 two-sided ideal $\mathfrak{a},\mathfrak{b},\mathfrak{c}$가 주어졌다 하자. 그럼 $(\mathfrak{a}\mathfrak{b})\mathfrak{c}$의 임의의 원소는
\[\left(\sum_{i=1}^{n_1} x_i^{(1)}y_i^{(1)}\right)z_1+\cdots+\left(\sum_{i=1}^{n_k}x_i^{(k)}y_i^{(k)}\right)z_k\]의 꼴로 쓰일 수 있으며, 분배법칙을 이용하여 이를 모두 풀어준 후 오른쪽 두 개를 묶어주면 이 원소가 $\mathfrak{a}(\mathfrak{b}\mathfrak{c})$에 속하는 것을 알 수 있다. 반대 방향 포함관계도 똑같은 방식으로 증명할 수 있으므로, 곱셈이 결합법칙을 만족한다. 또, 임의의 two-sided ideal $\mathfrak{a}$에 대해 $A \mathfrak{a}=\mathfrak{a}A=\mathfrak{a}$임이 자명하다.
마지막으로 임의의 $b_1+c_1,\ldots, b_n+c_n\in \mathfrak{b}+\mathfrak{c}$에 대하여
\[a_1(b_1+c_1)+\cdots a_n(b_n+c_n)\]을 분배법칙을 사용하여 풀어주면 $\mathfrak{a}(\mathfrak{b}+\mathfrak{c})\subset \mathfrak{a}\mathfrak{b}+\mathfrak{a}\mathfrak{c}$를 쉽게 보일 수 있다. 거꾸로 임의의
\[a_1b_1+\cdots a_nb_n + a_1'c_1+\cdots +a_m'c_m\in \mathfrak{a}\mathfrak{b}+\mathfrak{a}\mathfrak{c}\]에 대하여, $b_i$들과 $c_i$들이 모두 $\mathfrak{b}+\mathfrak{c}$의 원소이므로 위의 원소는 $\mathfrak{a}(\mathfrak{b}+\mathfrak{c})$의 원소이다. 비슷하게 오른쪽 분배법칙도 증명할 수 있다.
즉 $A$의 two-sided ideal들의 모임은 덧셈에 대한 역원만 제외하면 ring과 같은 구조를 갖는다. 이러한 구조를 semiring이라 부르는데, 특별히 사용할 일은 별로 없다.
임의의 두 two-sided ideal $\mathfrak{a},\mathfrak{b}$에 대하여, 다음 두 식
\[\mathfrak{a}\mathfrak{b}\subset \mathfrak{a}A\subset \mathfrak{a},\quad \mathfrak{a}\mathfrak{b}\subset A \mathfrak{b}\subset \mathfrak{b}\]이 모두 성립하므로 $\mathfrak{a}\mathfrak{b}\subset \mathfrak{a}\cap \mathfrak{b}$이 성립한다. 일반적으로 등호가 성립할 필요는 없지만, 특수한 경우에는 이것이 성립할 수도 있다.
명제 3 $A$의 two-sided ideal들 $\mathfrak{a},\mathfrak{b}_1,\ldots, \mathfrak{b}_n$이 주어졌다 하고, $A=\mathfrak{a}+\mathfrak{b}_i$가 모든 $i$에 대해 성립한다 가정하자. 그럼
\[A=\mathfrak{a}+\mathfrak{b}_1\cdots \mathfrak{b}_n=\mathfrak{a}+(\mathfrak{b}_1\cap\cdots\cap \mathfrak{b}_n)\]이 성립한다.
증명
어차피 $\mathfrak{b}_1\cdots \mathfrak{b}_n\subset \mathfrak{b}_1\cap \cdots\cap \mathfrak{b}_n$이므로 등식 $A=\mathfrak{a}+\mathfrak{b}_1\cdots \mathfrak{b}_n$만 보이면 충분하다. 또, 귀납적으로 증명이 가능하므로 $n=2$인 경우만 생각하면 충분하다. 즉 $A=\mathfrak{a}+\mathfrak{b}_1=\mathfrak{a}+\mathfrak{b}_2$라 하고, $A=\mathfrak{a}+\mathfrak{b}_1 \mathfrak{b}_2$임을 보이자.
우선 $A=\mathfrak{a}+\mathfrak{b}_1=\mathfrak{a}+\mathfrak{b}_2$로부터, $1=a+b_1=a’+b_2$를 만족하는 $a,a’\in \mathfrak{a}, b_i\in \mathfrak{b}_i$를 택할 수 있다. 그럼
\[1=a'+b_2=a'+1b_2=a'+(a+b_1)b_2=(a+a'b_2)+b_1b_2\in \mathfrak{a}+\mathfrak{b}_1 \mathfrak{b}_2\]이 성립한다.
이를 이용하면 다음 명제를 보일 수 있으며, 이는
명제 4 $A$의 two-sided ideal들 $\mathfrak{b}_1,\ldots, \mathfrak{b}_n$이 $\mathfrak{b}_i+\mathfrak{b}_j=A$ ($i\neq j$)를 항상 만족한다 하자. 그럼 다음 식
\[\mathfrak{b}_1\cap \cdots\cap \mathfrak{b}_n=\sum_{\sigma\in S_n} \mathfrak{b}_{\sigma(1)}\cdots \mathfrak{b}_{\sigma(n)}\]이 성립하며, 따라서 특히 $A$가 commutative이면
\[\mathfrak{b}_1\cap \cdots\cap \mathfrak{b}_n=\mathfrak{b}_1\cdots \mathfrak{b}_n\]이 성립한다.
증명
마찬가지로 귀납법을 이용해 증명한다. 우선 $n=2$인 경우, $b_1+b_2=1$을 만족하는 $b_i\in \mathfrak{b}_i$를 찾을 수 있다. 이제 임의의 $x\in \mathfrak{b}_1\cap \mathfrak{b}_2$에 대하여,
\[x=x\cdot 1=x(b_1+b_2)=xb_1+xb_2\in \mathfrak{b}_2 \mathfrak{b}_1+\mathfrak{b}_1 \mathfrak{b}_2\]이 성립한다. 이제 $n$보다 작은 모든 정수에 대해 원하는 식이 성립한다 가정하자. 우선 $\mathfrak{b}_n=\mathfrak{a}$와 $\mathfrak{b}_1,\ldots, \mathfrak{b}_{n-1}$에 앞선 명제 3을 적용하면
\[A=\mathfrak{b}_n+(\mathfrak{b}_1\cap\cdots\cap \mathfrak{b}_{n-1})=\mathfrak{b}_n+\mathfrak{b}_1\cdots \mathfrak{b}_{n-1}\]이 성립하므로, 두 아이디얼 $\mathfrak{b}_n$과 $\mathfrak{b}_1\cap\cdots\cap\mathfrak{b}_{n-1}$에 대해
\[\mathfrak{b}_n\cap(\mathfrak{b}_1\cap\cdots\cap\mathfrak{b}_{n-1})=(\mathfrak{b}_1\cap\cdots\cap\mathfrak{b}_{n-1})\mathfrak{b}_n+\mathfrak{b}_n(\mathfrak{b}_1\cap\cdots\cap\mathfrak{b}_{n-1})\]이 성립한다. 귀납적 가정에 의해 $\mathfrak{b}_1\cap\cdots\cap\mathfrak{b}_{n-1}=\sum_{\sigma\in S_{n-1}}\mathfrak{b}_{\sigma(1)}\cdots\mathfrak{b}_{\sigma(n-1)}$이 성립하므로, 이로부터
\[\mathfrak{b}_n\cap(\mathfrak{b}_1\cap\cdots\cap\mathfrak{b}_{n-1})=\left(\sum_{\sigma\in S_{n-1}}\mathfrak{b}_{\sigma(1)}\cdots\mathfrak{b}_{\sigma(n-1)}\right)\mathfrak{b}_n+\mathfrak{b}_n\left(\sum_{\sigma\in S_{n-1}}\mathfrak{b}_{\sigma(1)}\cdots \mathfrak{b}_{\sigma(n-1)}\right)\]이며, 이 때 우변은 합 $\sum_{\sigma\in S_n}\mathfrak{b}_{\sigma(1)}\cdots \mathfrak{b}_{\sigma(n)}$의 부분합이므로 원하는 결론을 얻는다.
환의 직접곱
Ring들의 family $(A_i)_{i\in I}$가 주어졌다 하자. 그럼 이들의 product $\prod A_i$ 위에 덧셈과 곱셈을 성분별로 정의하여 $\prod A_i$에 ring 구조를 줄 수 있다. 이는 §군의 직접곱, ⁋정의 1과 마찬가지 universal property를 만족한다. 즉,
임의의 ring $B$와 ring homomorphism들 $f_i:B \rightarrow A_i$들이 주어졌을 때, $f_i=\pr_i\circ f$이도록 하는 유일한 ring homomorphism $f:B \rightarrow \prod A_i$이 존재한다.
중국인의 나머지 정리
Ring $A$와, $A$의 two-sided ideal들 $\mathfrak{a}_i$가 주어졌다 하자. 그럼 projection들 $\pi_i:A \rightarrow A/\mathfrak{a}_i$이 존재하며, 이들로부터 ring homomorphism $\pi:A \rightarrow\prod A/\mathfrak{a}_i$가 정의된다.
명제 5 Ring $A$와, $A$의 two-sided ideal들 $\mathfrak{a}_1,\ldots, \mathfrak{a}_n$이 주어졌다 하자. 만일 $i\neq j$에 대하여 $\mathfrak{a}_i+\mathfrak{a}_j=A$가 항상 성립한다면 위에서 정의한 $\pi:A \rightarrow \prod_1^n A/\mathfrak{a}_i$는 surjective이고, 이 map의 kernel은 $\bigcap \mathfrak{a}_i$와 같다.
증명
우선 $\ker\pi=\bigcap \mathfrak{a}_i$인 것은 자명하므로, $\pi$가 surjective임을 보이면 충분하다. 이는 다음과 같이 귀납법으로 보일 수 있다.
우선 $n=1$인 경우는 quotient ring의 성질로부터 자명하다. 이제 적당한 $y\in A$가 존재하여, 모든 $i=1,\ldots, n-1$에 대해 $\pi_i(y)=x_i+\mathfrak{a}_i$가 성립한다 하자. 만일 모든 $i=1,\ldots, n$에 대해 $\pi_i(x)=x_i+\mathfrak{a}_i$를 만족하는 $x\in A$가 존재한다면, 적당한 $z\in A$에 대해 $x=y+z$라 쓸 수 있고, 이 때 $x$와 $y$의 조건으로부터 $z\in\bigcap_{i=1}^{n-1} \mathfrak{a}_i$가 성립하여야 한다. 또, $z+\mathfrak{a}_n=x_n-y \mathfrak{a}_n$이 성립하여야 하며, 거꾸로 이러한 $z$가 존재한다면 $x=y+z$가 원하는 $x$가 된다. 그런데 명제 3으로부터 $\mathfrak{a}_n+\bigcap_1^{n-1} \mathfrak{a}_i=A$이 성립하므로 이러한 $z$를 반드시 찾을 수 있다.
따라서, first isomorphism theorem에 의하여 다음의 canonical isomorphism
\[\frac{A}{\bigcap_{i=1}^n \mathfrak{a}_i}\cong \prod_{i=1}^n A/\mathfrak{a}_i\]이 존재하며, 만일 $A$가 commutative라면 명제 4에 의하여
\[A/\mathfrak{a}_1\cdots \mathfrak{a}_n\cong\prod_{i=1}^n A/\mathfrak{a}_i\]으로 쓸 수 있다. 특히 $\bigcap \mathfrak{a}_i=0$이라면 isomorphism $A\cong\prod A/\mathfrak{a}_i$를 얻는다.
특별히 $A=\mathbb{Z}$인 경우를 생각하고, 쌍마다 서로소인 $n_1,\ldots, n_r$에 대해 $\mathfrak{a}_i=n_i \mathbb{Z}$라 하자. $n=n_1\cdots n_r$이라 하면, 위의 명제와 first isomorphism theorem에 의하여 isomorphism $\mathbb{Z}/n \mathbb{Z}\cong\prod \mathbb{Z}/n_i \mathbb{Z}$을 얻는다. 즉 위의 명제로부터 원래의 중국인의 나머지 정리를 얻어낼 수 있다.
더 일반적으로 다음이 모두 동치이다.
명제 6 Ring $A$와, $A$의 center $C(A)$, 그리고 two-sided ideal들 $\mathfrak{a}_1,\ldots, \mathfrak{a}_n$이 주어졌다 하자. 다음이 모두 동치이다.
- 위에서 정의한 $A \rightarrow \prod A/\mathfrak{a}_i$가 isomorphism이다.
- 모든 $i\neq j$에 대하여 $\mathfrak{a}_i+\mathfrak{a}_j=A$이고 $\bigcap \mathfrak{a}_i=0$이다.
- 모든 $i\neq j$에 대하여 $\mathfrak{a}_i+\mathfrak{a}_j=A$이고 $\prod \mathfrak{a}_i=0$이다.
- $C(A)$의 원소들 $e_1,\ldots, e_n$이 존재하여 $\sum e_i=1$이며, 모든 $i$에 대하여 $e_i^2=e_i$, 모든 $i\neq j$에 대하여 $e_ie_j=0$이 성립하고, 모든 $i$에 대해 $\mathfrak{a}_i=A(1-e_i)$이다.
증명
마지막 조건의 $e_i$들은 $\prod A/\mathfrak{a}_i$의 각 성분 중, $i$번째 성분만 $1$이고 나머지는 모두 $0$인 원소들을 의미한다. 이를 염두에 두면 네 조건이 모두 동치라는 것을 쉽게 보일 수 있다.

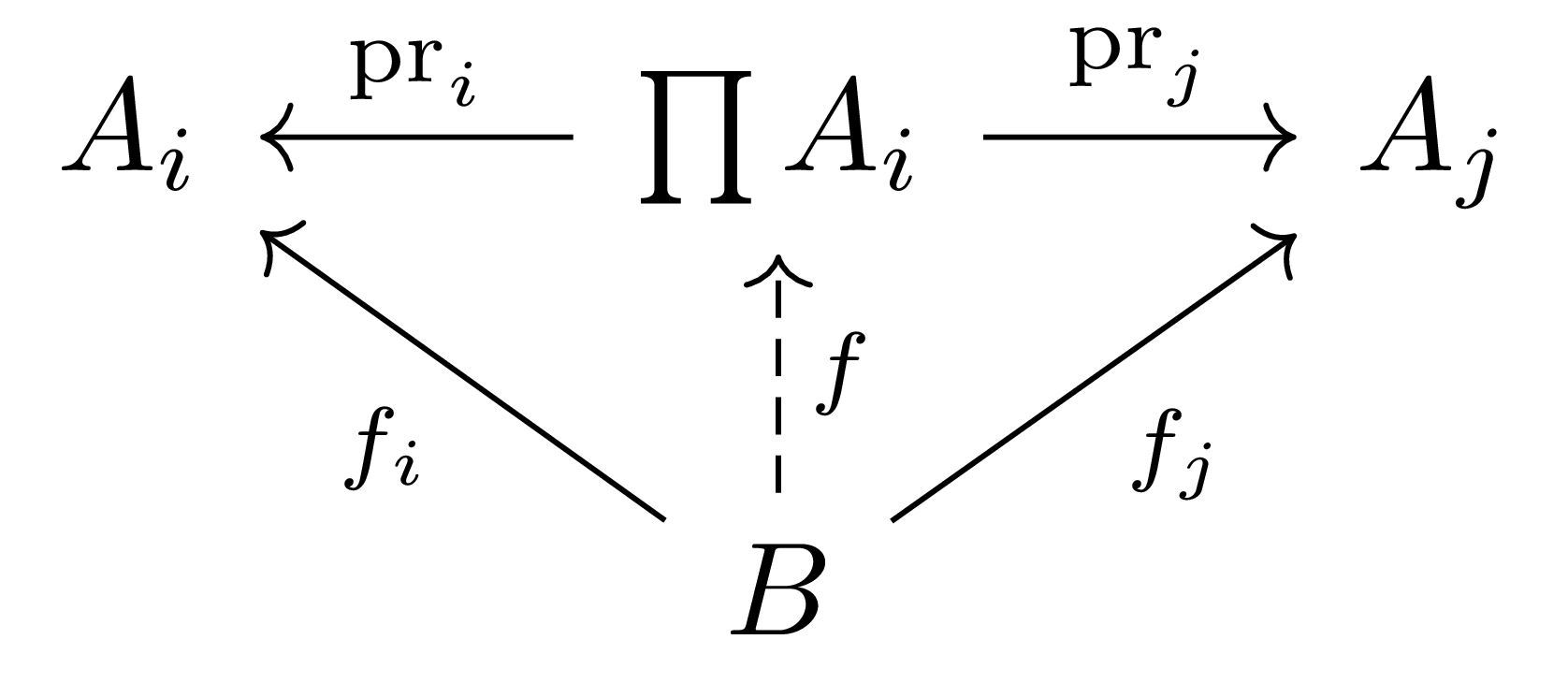
댓글남기기