이번 글에서 우리는 행렬과 이들 사이의 연산을 정의한다.
행렬의 기본 정의
간단하게 이야기해서, $m\times n$ 행렬은 $mn$개의 스칼라들을 $m\times n$ 사각형 모양으로 적은 것이다. 즉, 행렬 $A$에 대하여 $i$번째 행, $j$번째 열에 해당하는 $A$의 성분을 $A_{ij}$로 표기하기로 한다면, 행렬은 다음과 같이 나타낼 수 있다.
\[A=\begin{pmatrix}A_{11}&A_{12}&\cdots&A_{1n}\\A_{21}&A_{22}&\cdots&A_{2n}\\ \vdots&\vdots&\ddots&\vdots\\A_{m1}&A_{m2}&\cdots&A_{mn}\end{pmatrix}\]위의 행렬 $A$에서, $m$개의 벡터들
\[(A_{11},A_{12},\cdots, A_{1n}),\;\ldots,\;(A_{m1},A_{m2},\cdots,A_{mn})\]을 $A$의 행 (row)이라고 하고, $n$개의 벡터들
\[(A_{11},A_{21},\cdots,A_{m1}),\; \ldots,\; (A_{1n}, A_{2n},\cdots, A_{mn})\]을 $A$의 열 (column)들이라고 한다. 여기서 행벡터들은 모두 $n$차원 공간 $F^n$의 원소들이고, 열벡터들은 $m$차원 공간 $F^m$의 원소들이다.
종종 행렬의 특정한 블럭들을 묶어서 다음과 block form으로 쓰는 것이 편할 때가 있다. 예컨대, 다음의 행렬
\[\begin{pmatrix}0&0&1\\ 0&0&3\\ 2&4&0\end{pmatrix}\]은 아래의 모양
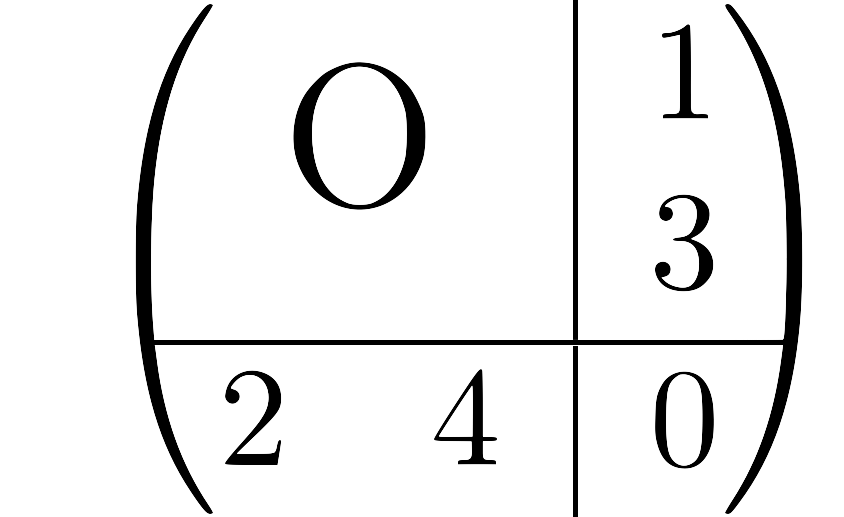
과 같이 편하게 쓸 수 있다. 이와 비슷하게, 우리는 위의 $m\times n$ 행렬 $A$에서 각각의 열벡터들 $A_1$, $A_2$, $\ldots$, $A_n$를 이용하여
\[A=(A_1|A_2|\cdots|A_n)\]과 같이 쓸 수도 있다. 각 성분이 $\mathbb{k}$의 원소인 모든 $m\times n$ 행렬들의 집합은 $\Mat_{m\times n}(F)$로 적는다. 특별히 $\Mat_{m\times m}(F)$은 간략하게 $\Mat_m(F)$로 적는다.
행렬의 연산
행렬들 간에는 덧셈과 곱셈이 정의되지만, 임의의 원소들에 대하여 덧셈과 곱셈이 잘 정의되는 것은 아니다. 예를 들어, 덧셈은 모양이 같은 행렬들에 대해서만 각 성분별 합으로 정의된다. 즉, $\Mat_{m\times n}(F)$는 잘 정의된 덧셈을 가지고 있다. 여기에 더해, 각 행렬에 대한 상수곱을 다음의 식
\[\alpha\begin{pmatrix}A_{11}&A_{12}&\cdots&A_{1n}\\A_{21}&A_{22}&\cdots&A_{2n}\\ \vdots&\vdots&\ddots&\vdots\\A_{m1}&A_{m2}&\cdots&A_{mn}\end{pmatrix}=\begin{pmatrix}\alpha A_{11}&\alpha A_{12}&\cdots&\alpha A_{1n}\\\alpha A_{21}&\alpha A_{22}&\cdots&\alpha A_{2n}\\ \vdots&\vdots&\ddots&\vdots\\\alpha A_{m1}&\alpha A_{m2}&\cdots&\alpha A_{mn}\end{pmatrix}\]으로 정의한다면, 어렵지 않게 $\Mat_{m\times n}(F)$가 $\mathbb{k}$-벡터공간 구조를 갖는다는 것을 확인할 수 있다. 이 벡터공간은 $mn$차원이 된다. Basis는 물론, 다음과 같은 행렬들
\[\begin{pmatrix}1&0&\cdots&0\\0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&0\end{pmatrix},\quad\begin{pmatrix}0&1&\cdots&0\\0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&0\end{pmatrix},\quad\cdots,\quad\begin{pmatrix}0&0&\cdots&0\\0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&1\end{pmatrix}\]로 잡는 것이 가장 단순할 것이다. 행렬의 곱셈은 이보다 조금 더 복잡해서, 우리는 우선 행렬과 벡터의 곱부터 정의해야 한다.
정의 2 $A\in\Mat_{m\times n}(F)$이고 $x\in\mathbb{k}^n$이라 하자. 그럼 행렬 $A$와 벡터 $x$의 곱 $Ax$는 다음의 식
\[Ax=\sum_{j=1}^nx_j A_j\]으로 정의된다. 여기서 $x_j$는 $x$의 $j$번째 성분, $A_j$는 $A$의 $j$번째 열벡터이다.
위 정의에 의해 $Ax$는 임의의 벡터 $x$에 대해서
위의 식을 조금 더 풀어 쓸 수 있다. 열벡터 $A_j$의 $i$번째 성분을 $A_{ij}$라 하자. 그럼 벡터 $Ax$의 첫 번째 성분은 벡터 $x_jA_j$들의 첫 번째 성분의 합으로 나타나므로
\[x_1A_{11}+x_2A_{12}+\cdots+x_nA_{1n}\]이라 쓸 수 있으며, 더 일반적으로 $Ax$의 $i$번째 성분은
\[x_1A_{i1}+x_2A_{i2}+\cdots+x_nA_{in}\]으로 나타난다. 따라서 명시적으로는 다음의 식
\[\begin{pmatrix}A_{11}&A_{12}&\cdots&A_{1n}\\A_{21}&A_{22}&\cdots&A_{2n}\\\vdots&\vdots&\ddots&\vdots\\A_{m1}&A_{m2}&\cdots&A_{mn}\end{pmatrix}\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}=\begin{pmatrix}\sum_{i=1}^nA_{1i}x_i\\\sum_{i=1}^nA_{2i}x_i\\\vdots\\\sum_{i=1}^nA_{mi}x_i\end{pmatrix}\]을 얻는다.
행렬의 곱
행렬과 벡터의 곱을 정의하였으므로, 우리는 이제 행렬과 행렬 사이의 곱을 정의할 수 있다.
정의 3 두 행렬 $A\in \Mat_{m\times n}(F)$, $B\in\Mat_{p\times q}(F)$에 대하여, 행렬의 곱 $BA$가 정의되기 위한 필요충분조건은 $q=m$인 것이다. 이 때, 행렬의 곱 $BA$는 다음의 식
\[BA=(BA_1|BA_2|\cdots|BA_n)\]으로 주어진다. ($A_i$는 $A$의 $i$번째 열, $BA_i$는 열벡터 $A_i$와 행렬 $B$의 곱1)
즉 $A_j$의 $i$번째 성분을 $A_{ij}$라 표현하면
\[BA_j=\sum_{k=1}^m A_{kj}B_k\]이라 쓸 수 있다. 이 때 열벡터 $BA_j$의 $i$번째 성분, 즉 행렬 $BA$의 $(i,j)$번째 성분인 $(BA)_{ij}$는
\[(BA)_{ij}=\sum_{k=1}^n B_{ik}A_{kj}\]로 주어진다.
행렬의 곱은 교환법칙을 만족하지 않는다. 즉, $AB=BA$는 일반적으로 성립하지 않는다. $BA$가 정의된다고 해서 $AB$가 정의된다는 보장도 없을 뿐더러, 이 둘이 모두 정의된다고 해도 $AB$와 $BA$는 다른 모양을 가질 수 있으며, $m=n=p=q$가 성립하여 $AB$, $BA\in\Mat_{m\times m}(F)$라 하더라도 이 값이 다를 수도 있다.
반면 행렬의 곱은 결합법칙을 만족한다. 행렬 $A,B,C$가 $AB$, $BC$가 모두 정의되도록 하는 행렬들이라면, 행렬의 곱 $A(BC)$와 $(AB)C$ 또한 잘 정의되며 이 때
\[A(BC)=(AB)C\]가 성립한다.
정의 4 행렬 $I=(e_1|e_2|\cdots|e_n)$을 $n\times n$ 항등행렬이라 부른다.
즉,
\[I=\begin{pmatrix}1&0&\cdots&0\\0&1&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&1\end{pmatrix}\]이다. 이와 비슷하게, 대각성분을 제외한 모든 성분이 $0$인 행렬을 대각행렬diagonal matrix이라 부른다.
그 이름에 걸맞게, $I$가 $n\times n$ 항등행렬이라면 임의의 $m\times n$ 행렬 $A$에 대하여 $AI=A$, 그리고 임의의 $n\times m$ 행렬 $B$에 대해 $IB=B$가 성립한다.
정의 5 $A\in\Mat_n(F)$인 행렬이라 하자. $A$가 가역invertible이라는 것은, 어떠한 $B\in\Mat_n(F)$가 존재하여 $AB=BA=I$인 것이다. 가역이 아닌 행렬을 singular matrix특이행렬라 부른다.
$\Mat_n(F)$의 임의의 원소는 가역일 필요가 없다. 예로 영행렬 $O$는 가역이 아니다. 따라서 $\Mat_n(F)$는 일반적으로 abelian group이 되지 않는다. 그 대신,
정의 6 $n\times n$ 가역행렬들의 집합에 행렬곱으로 연산이 주어진 group을 $\GL(n,F)$로 적고, general linear group이라 부른다.
위에서 언급한 것과 같이, 행렬의 곱은 결합법칙을 만족한다. 즉 $\GL(n,F)$의 연산은 결합법칙을 만족한다. 또, $\GL(n,F)$의 항등원은 항등행렬 $I$이고, $A\in\GL(n,F)$의 역원은 정의 5의 정의에서 등장하는 행렬 $B$이다. 이제 §가환군과 체, ⁋명제 2의 유일성으로부터 $A$의 역원은 유일하다는 것을 안다. 이를 $A$의 역행렬inverse matrix라 부르고 $A^{-1}$로 표기한다. 다음의 관찰
\[(B^{-1}A^{-1})AB=B^{-1}IB=B^{-1}B=I\]로부터, 두 가역행렬의 곱 $AB$도 가역행렬이며 그 역행렬은 $B^{-1}A^{-1}$임을 알 수 있다.
$A$의 역행렬이 $n\times n$ 가역행렬에 대해서만 정의되는 이유를 생각해보자. 만일 $m\times n$ 행렬 $A$의 역행렬이 존재한다면, $AB$와 $BA$가 모두 존재해야 하므로 $A$의 역행렬은 반드시 $n\times m$ 행렬이어야 하며, 이는
\[AB=I_m,\qquad BA=I_n\]을 만족해야 한다. 이러한 행렬 $B$는 존재하지 않는다. 이는 §선형대수학의 기본정리에 의해 자명하게 따라나오는 결과지만, 오직 행렬의 언어만으로도 증명할 수 있다.
정의 7 $A\in\Mat_n(F)$라 하자. 그럼 $A$의 대각합trace $\tr(A)$는 $A$의 대각성분들의 합, 즉 $\tr(A)=\sum_1^n A_{ii}$으로 정의된다.
이렇게 정의된 $\tr$은 $\Mat_n(F)$에서 $\mathbb{k}$로의 linear map이다. 즉 임의의 $A,B\in\Mat_n(F)$과 $\alpha\in\mathbb{k}$에 대하여
\[\tr(A+B)=\tr(A)+\tr(B),\qquad \tr(\alpha A)=\alpha\tr(A)\]이 성립한다.
이제 두 행렬 $A\in\Mat_{m\times n}(F)$과 $B\in\Mat_{n\times m}(F)$이 주어졌다 하자. 그럼
\[\tr(AB)=\sum_{i=1}^m(AB)_{ii}=\sum_{i=1}^m\sum_{j=1}^nA_{ij}B_{ji}=\sum_{j=1}^n\sum_{i=1}^m B_{ji}A_{ij}=\sum_{j=1}^n(BA)_{jj}=\tr(BA)\]임을 확인할 수 있다. 따라서 만일 $AB=I_m$이고 $BA=I_n$이라면 위의 식에서
\[m=\tr(I_m)=\tr(AB)=\tr(BA)=\tr(I_n)=n\]이어야 하므로, $m\neq n$이라면 이를 만족하는 행렬 $B$는 존재하지 않는다.
정의 8 주어진 행렬 $A\in\Mat_{m\times n}(F)$에 대해서, $A$의 전치행렬transpose $A^t$는 다음의 식
\[(A^t)_{ij}=A_{ji}\]으로 정의된 $n\times m$ 행렬이다.
명제 9 두 행렬 $A\in\Mat_{m\times n}(F),B\in\Mat_{n\times k}(F)$에 대하여, 다음의 식
\[(AB)^t=B^tA^t\]가 성립한다.
이는 단순한 계산을 통해 확인할 수 있다.
참고문헌
[Goc] M.S. Gockenbach, Finite-dimensional linear algebra, Discrete Mathematics and its applications, Taylor&Francis, 2011.
[Lee] 이인석, 선형대수와 군, 서울대학교 출판문화원, 2005.
-
위의 정의에 의하여, 행렬 $BA$의 $j$번째 열은 행렬 $B$와 열벡터 $A_j$의 곱과 같고, 따라서 $BA_j$를
$BA$의 $j$번째 열 로 생각하든 $B$와 $A_j$의 곱으로 생각하든 혼동의 여지가 없다. ↩

댓글남기기