우리는 선형대수학의 기본정리로부터, 두 $\mathbb{k}$-벡터공간 $V,W$에 basis의 선택이 주어진다면 임의의 linear map $L:V\rightarrow W$를 그 행렬표현 $[L]_\mathcal{C}^\mathcal{B}$와 동일하게 취급할 수 있다는 것을 살펴보았다. 이제 우리는 basis가 바뀌었을 때 이 표현들이 어떻게 바뀌는지를 살펴본다.
정의 1 임의의 유한차원 $\mathbb{k}$-벡터공간 $V$와, $V$의 두 basis $\mathcal{B},\mathcal{B}’$에 대하여, $\mathcal{B}$에서 $\mathcal{B}’$로의 기저변환행렬change-of-basis matrix은
\[[\id_V]_{\mathcal{B}'}^\mathcal{B}\]를 의미한다.
벡터공간의 차원이 잘 정의된다는 것으로부터 이러한 행렬은 반드시 정사각행렬이 되어야 한다는 것이 자명하다. 또, 다음의 식
\[I=[\id_V]^{\mathcal{B}}_{\mathcal{B}}=[\id_V]_{\mathcal{B}}^{\mathcal{B}'}[\id_V]^\mathcal{B}_{\mathcal{B}'}\]으로부터 이러한 행렬은 항상 가역이라는 것을 알 수 있다.
Change-of-basis matrix가 어떤 방식으로 작동하는지를 살펴보기 위해, 유한차원 $\mathbb{k}$-벡터공간 $V$를 고정하고, $V$ 위에 정의된 두 basis $\mathcal{B},\mathcal{B}’$가 주어졌다 하자. 선형대수학의 기본정리는 다음의 diagram이 commute한다는 것을 의미한다.
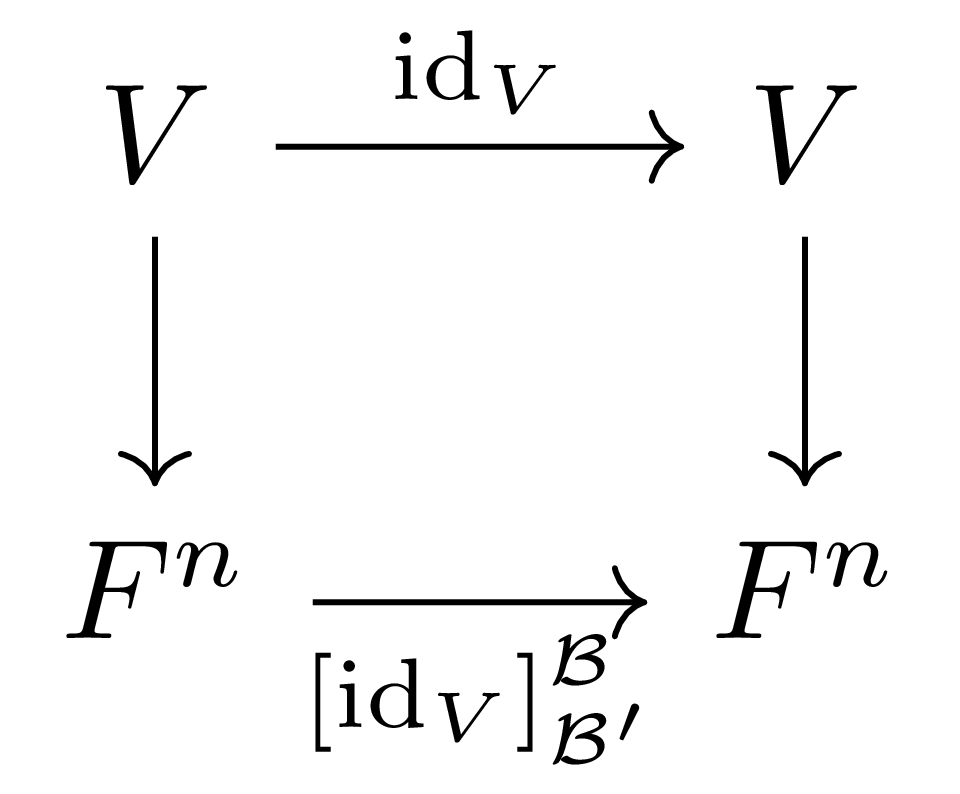
이 때 두 개의 수직방향 함수는 각각 $v\mapsto [v]_\mathcal{B}$와 $v\mapsto[v]_{\mathcal{B}’}$를 의미한다. 따라서 기저변환행렬은 $v\in V$의 $\mathcal{B}$에 대한 좌표표현을 받아, $\mathcal{B}’$에 대한 좌표표현으로 바꾸어주는 행렬이라 생각할 수 있다. 더 일반적으로 임의의 linear map $L:V\rightarrow W$가 주어졌다 하고, $V,W$의 basis $\mathcal{B},\mathcal{C}$, 그리고 또 다른 basis $\mathcal{B}’,\mathcal{C}’$가 주어졌다 하면, 선형대수학의 기본정리로부터 다음의 식
\[[L]_{\mathcal{C}'}^{\mathcal{B}'}=[\id_W]_{\mathcal{C}'}^\mathcal{C}[L]_{\mathcal{C}}^\mathcal{B}[\id_V]^{\mathcal{B}'}_{\mathcal{B}}\]를 얻는다.
두 $m\times n$ 행렬 $A,B$가 주어졌다 하자. 그럼 위의 식에서부터, 만일 적당한 두 가역행렬 $P,Q$가 존재하여 다음의 식
\[B=PAQ\]를 만족한다면 $A$와 $B$를 같은 것으로 취급하고 싶은 유혹이 있다. 이는 고정된 linear map $L$이 주어졌을 때, $L$의 정의역과 공역의 basis를 잘 택하여 얻어지는 행렬표현들을 모두 같은 것으로 생각한다는 것이다.
그러나 이렇게 그럴듯한 동기에 비해 그 결과는 별로 좋지 않다. $L$의 정의역과 공역의 basis를 모두 변화시킬 수 있다면, 정의역의 임의의 basis $\{x_1,\ldots, x_n\}$을 택하고, 이후 공역에서는 $L(x_1),\ldots, L(x_n)$들 중 일차독립인 $L(x_1),\ldots, L(x_k)$를 택한 후 §벡터공간의 차원, ⁋명제 6을 이용하여 공역의 basis를 만들면 이 linear map은 항상 블록행렬
\[\begin{pmatrix}I&O\\O&O\end{pmatrix}\]꼴로 나타낼 수 있기 때문이다. 즉, 이런 식으로 $L$의 행렬표현을 분류한다면 여기에 영향을 미치는 것은 오직 $L$의 rank 뿐이다.
따라서 우리는 이 동치관계보다 세밀한 관계를 정의해야 한다.
정의 2 임의의 $n\times n$ 행렬 $A,B$가 주어졌다 하자. 그럼 $A$와 $B$가 닮은 행렬similar matrix이라는 것은 적당한 가역행렬 $P$가 존재하여 $A=PBP^{-1}$이 성립하는 것이다.
즉 행렬 $A,B$가 닮은 행렬이라는 것은, 고정된 벡터공간 $V$에 대해 $A$를
이 된다.
아직은 행렬들 간의 닮음이 충분히 좋은 동치관계라는 것을 느끼기 어렵지만, 행렬식을 정의한 후에는 이것이 충분히 좋은 동치관계라는 것을 확인할 수 있다.
참고문헌
[Lee] 이인석, 선형대수와 군, 서울대학교 출판문화원, 2005.

댓글남기기