지난 글에서 각각 $n$차원, $m$차원인 두 $\mathbb{k}$-벡터공간 $V,W$에 대하여 $\Hom(V,W)$는 $mn$차원 $\mathbb{k}$-벡터공간이 된다는 것을 살펴보았다. 또 $m\times n$ 행렬들의 공간 $\Mat_{m\times n}(F)$ 또한 $mn$차원의 $\mathbb{k}$-벡터공간이다. 그럼 §동형사상, ⁋따름정리 4로부터 이 두 벡터공간이 isomorphic하다는 것을 안다.
이번 글에서 증명할 선형대수학의 기본정리1는 이들이 단순히 같은 차원을 갖는 벡터공간이기 때문에 isomorphic할 뿐만 아니라, 이들 사이의
기본정리: 유클리드 공간
§선형사상들의 공간에서 우리는 다음의 식
\[\begin{aligned}L(x_1)&=\alpha_{11}y_1+\alpha_{21}y_2+\cdots+\alpha_{m1}y_m\\L(x_2)&=\alpha_{12}y_1+\alpha_{22}y_2+\cdots+\alpha_{m2}y_m\\&\phantom{a}\vdots\\L(x_n)&=\alpha_{1n}y_1+\alpha_{2n}y_2+\cdots+\alpha_{mn}y_m\end{aligned}\]을 만족하는 linear map $L$을 다음의 대응
\[v=\sum_{i=1}^n v_ix_i\quad\mapsto\quad \sum_{j=1}^m\left(\sum_{i=1}^n\alpha_{ji}v_i\right)y_j=L(v)\tag{1}\]으로 이해하기로 하였다. 특히 만일 $V=F^n$, $W=F^m$이고, 이들 각각에 standard basis $\mathcal{E}_n=\{e_1,\ldots, e_n\},\mathcal{E}_m=\{e_1,\ldots,e_m\}$가 주어졌다 하면 위의 대응은
\[\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}\quad\mapsto\quad\begin{pmatrix}\sum_{i=1}^n\alpha_{1i}v_i\\\sum_{i=1}^n\alpha_{2i}v_i\\\vdots\\\sum_{i=1}^n\alpha_{mi}v_i\end{pmatrix}\]으로 쓸 수 있다. 그런데 우변은 정확히 행렬과 벡터의 곱
\[\begin{pmatrix}\alpha_{11}&\alpha_{12}&\cdots&\alpha_{1n}\\\alpha_{21}&\alpha_{22}&\cdots&\alpha_{2n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m1}&\alpha_{m2}&\cdots&\alpha_{mn}\end{pmatrix}\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}\tag{2}\]과 동일한 모양이다. 위의 식에서의 $m\times n$ 행렬을 $\mathcal{E}_n,\mathcal{E}_m$에 대한 $L$의 행렬표현이라 부르고, 이를 $[L]^{\mathcal{E}_n}_{\mathcal{E}_m}$로 적는다.
반대로 $m\times n$ 행렬은 똑같은 방식으로 linear map을 지정해준다는 것을 확인할 수 있다.
예시 1 유클리드 $n$-공간 $F^n$과, 행렬 $A\in\Mat_{m\times n}(F)$를 생각하자. 임의의 $x\in\mathbb{k}^n$에 대하여, $L_A(x)$를 다음의 식
\[L_A(x)=Ax\]으로 정의하면, $L_A$는 $F^n$에서 $F^m$으로의 linear map이 된다.
$F^n$에서 $F^m$으로의 임의의 linear map $L$이 주어졌다 하자. 어렵지 않게 $L=L_{[L]^{\mathcal{E}_n}_{\mathcal{E}_m}}$임을 확인할 수 있다. 따라서 다음의 대응이 존재한다.
\[\{\text{linear maps from $F^n$ to $F^m$}\}\longleftrightarrow\Mat_{m\times n}(F)\]더 정확하게 말하자면 $L\mapsto [L]^{\mathcal{E}_n}_{\mathcal{E}_m}$, 그리고 $A\mapsto L_A$ (예시 1의 정의)이 서로의 역함수가 되는 전단사함수가 된다.
그런데 왼쪽의 집합은 $\Hom(F^n, F^m)$와 같으므로, 이 대응이 전단사인 linear map, 곧 isomorphism이 되는지를 확인해볼 수 있다. 이에 대한 답은 그렇다는 것이며, 이 다음의 정리 3과 함께 이 결과를 선형대수학의 기본정리라 부른다.
정리 2 $\Hom(F^n,F^m)\cong\Mat_{m\times n}(F)$
증명
주어진 함수 $L\mapsto[L]^{\mathcal{E}_n}_{\mathcal{E}_m}$가 linear임을 보여야 한다.
$L_1,L_2$가 모두 $\Hom(F^n,F^m)$의 원소라 하자. 그럼 각각의 $e_i\in\mathcal{E}_n$에 대하여,
\[\begin{aligned}L_1(e_1)&=\alpha_{1,1}e_1+\alpha_{2,1}e_2+\cdots+\alpha_{m,1}e_m\\L_1(e_2)&=\alpha_{1,2}e_1+\alpha_{2,2}e_2+\cdots+\alpha_{m,2}e_m\\&\vdots\\L_1(e_n)&=\alpha_{1,n}e_1+\alpha_{2,n}e_2+\cdots+\alpha_{m,n}e_m\end{aligned}\]그리고
\[\begin{aligned}L_2(e_1)&=\beta_{1,1}e_1+\beta_{2,1}e_2+\cdots+\beta_{m,1}e_m\\L_2(e_2)&=\beta_{1,2}e_1+\beta_{2,2}e_2+\cdots+\beta_{m,2}e_m\\&\vdots\\L_2(e_n)&=\beta_{1,n}e_1+\beta_{2,n}e_2+\cdots+\beta_{m,n}e_m\end{aligned}\]이도록 하는 스칼라들의 family $(\alpha_{i,j})$, $(\beta_{i,j})$들이 존재한다. 이제,
\[\begin{aligned}(L_1+L_2)(e_1)&=(\alpha_{1,1}+\beta_{1,1})e_1+(\alpha_{2,1}+\beta_{2,1})e_2+\cdots+(\alpha_{m,1}+\beta_{m,1})e_m\\(L_1+L_2)(e_2)&=(\alpha_{1,2}+\beta_{1,2})e_1+(\alpha_{2,2}+\beta_{2,2})e_2+\cdots+(\alpha_{m,2}+\beta_{m,2})e_m\\&\vdots\\(L_1+L_2)(e_n)&=(\alpha_{1,n}+\beta_{1,n})e_1+(\alpha_{2,n}+\beta_{2,n})e_2+\cdots+(\alpha_{m,n}+\beta_{m,n})e_m\end{aligned}\]이고, 따라서 $L_1+L_2$의 행렬표현 $[L_1+L_2]^{\mathcal{E}_n}_{\mathcal{E}_m}$은 정확히 $[L_1]^{\mathcal{E}_n}_{\mathcal{E}_m}+[L_2]^{\mathcal{E}_n}_{\mathcal{E}_m}$이 된다. 이와 유사하게 스칼라곱에 대한 것도 성립한다.
뿐만 아니라 행렬들의 곱 또한 $\Hom(F^n,F^m)$에서 특별한 의미를 갖는다.
정리 3 세 유클리드 공간들 $F^n,F^m,F^k$가 주어졌다 하자. 그럼 임의의 $L_1:F^n\rightarrow F^m$, $L_2:F^m\rightarrow F^k$에 대하여 항상
\[[L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}=[L_2]^{\mathcal{E}_m}_{\mathcal{E}_k}[L_1]^{\mathcal{E}_n}_{\mathcal{E}_m}\]이 성립한다. 즉, linear map의 합성은 행렬의 곱과 같다.
증명
좌변의 $[L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}$을 결정하기 위해서는 $L_2\circ L_1$에 의해 $\mathcal{E}_n$의 원소 $e_i$들이 어디로 옮겨지는지만 확인하면 된다. $L_1$, $L_2$가 다음의 식
\[[L_1]^{\mathcal{E}_n}_{\mathcal{E}_m}=\begin{pmatrix}\alpha_{1,1}&\alpha_{1,2}&\cdots&\alpha_{1,n}\\\alpha_{2,1}&\alpha_{2,2}&\cdots&\alpha_{2,n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m,1}&\alpha_{m,2}&\cdots&\alpha_{m,n}\end{pmatrix},\quad[L_2]^{\mathcal{E}_m}_{\mathcal{E}_k}=\begin{pmatrix}\beta_{1,1}&\beta_{1,2}&\cdots&\beta_{1,m}\\\beta_{2,1}&\beta_{2,2}&\cdots&\beta_{2,m}\\\vdots&\vdots&\ddots&\vdots\\\beta_{k,1}&\beta_{k,2}&\cdots&\beta_{k,m}\end{pmatrix}\]으로 주어졌다 하자. 약간의 계산을 하면,
\[\begin{aligned}(L_2\circ L_1)(e_i)&=L_2(\alpha_{1,i}e_1+\cdots+\alpha_{m,i}e_m)\\&=\alpha_{1,i}L_2(e_1)+\alpha_{2,i}L_2(e_2)+\cdots+\alpha_{m,i}L(e_m)\\&=\alpha_{1,i}(\beta_{1,1}e_1+\beta_{2,1}e_2+\cdots+\beta_{k,1}e_k)\\&\phantom{==}+\alpha_{2,i}(\beta_{1,2}e_1+\beta_{2,2}e_2+\cdots+\beta_{k,2}e_k)\\&\phantom{===}+\cdots\\&\phantom{====}+\alpha_{m,i}(\beta_{1,m}e_1+\beta_{2,m}e_2+\cdots+\beta_{k,m}e_k)\end{aligned}\]이제 위 식을 $F^k$의 basis $e_1,\ldots, e_k$들끼리 묶으면,
\[(L_2\circ L_1)(e_i)=\left(\sum_{l=1}^m\alpha_{l,i}\beta_{1,l}\right)e_1+\cdots+\left(\sum_{l=1}^m\alpha_{l,i}\beta_{k,l}\right)e_k.\]$[L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}$의 $i$번째 열은 $e_i$가 $L_2\circ L_1$에 의해 옮겨지는 벡터이므로, 행렬 $[L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}$의 $i$열, $j$행은 이 벡터의 $j$번째 성분 $\sum_{l=1}^m\alpha_{l,i}\beta_{j,l}$이 된다. 이제 §행렬, ⁋정의 3 직후의 계산으로부터 이것이 두 행렬 $[L_2]_{\mathcal{E}_k}^{\mathcal{E}_m}$, $[L_1]_{\mathcal{E}_m}^{\mathcal{E}_n}$의 곱의 $(i,j)$ 성분이라는 것을 안다.
기본정리: 일반적인 경우
앞서 우리가 증명한 기본정리는 유클리드 공간에 대해서만 적용되지만, 아주 작은 수정만 있으면 일반적인 유한차원 $\mathbb{k}$-벡터공간에 대해서도 성립한다. 이 과정은 다음의 diagram으로 간단하게 요약할 수 있다.
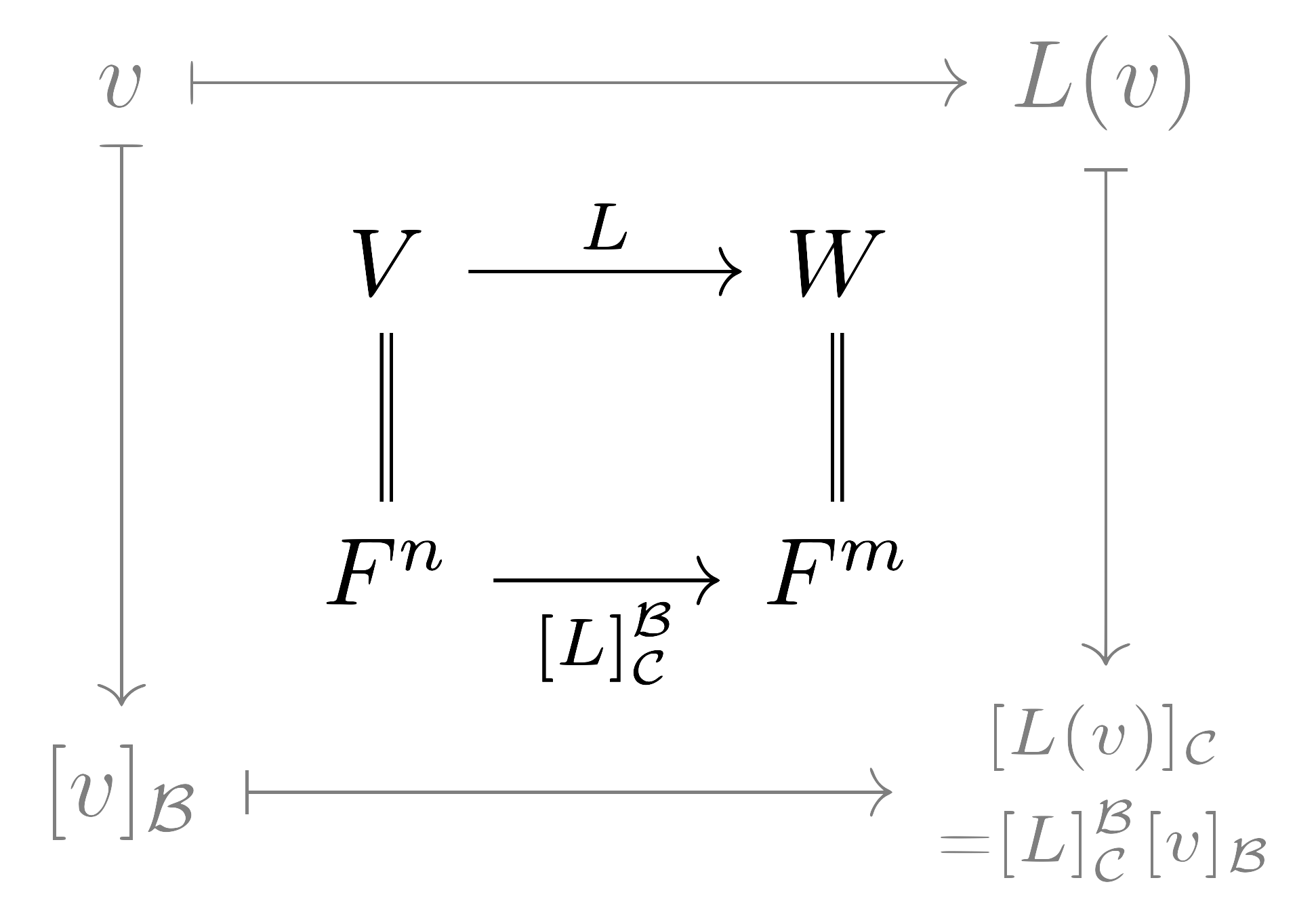
임의의 유한차원 $\mathbb{k}$-벡터공간 $V$와 그 basis $\mathcal{B}=\{x_1,\ldots, x_n\}$에 대해 정의된 좌표표현은 다음의 isomorphism
\[v=\sum_{i=1}^n v_ix_i\mapsto [v]_\mathcal{B}=\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}\in\mathbb{k}^n\]이다. 비슷하게 또 다른 유한차원 $\mathbb{k}$-벡터공간 $W$과 그 basis $\mathcal{C}=\{y_1,\ldots, y_m\}$가 주어졌다 하고, linear map $L:V\rightarrow W$가 다음의 식
\[\begin{aligned}L(x_1)&=\alpha_{1,1}y_1+\alpha_{2,1}y_2+\cdots+\alpha_{m,1}y_m\\L(x_2)&=\alpha_{1,2}y_1+\alpha_{2,2}y_2+\cdots+\alpha_{m,2}y_m\\&\vdots\\L(x_n)&=\alpha_{1,n}y_1+\alpha_{2,n}y_2+\cdots+\alpha_{m,n}y_m\end{aligned}\]에 의해 결정된다 하자. 그럼 $\mathcal{B},\mathcal{C}$에 대한 $L$의 행렬표현 $[L]^\mathcal{B}_\mathcal{C}$을 이번에는 다음의 식
\[[L]^\mathcal{B}_\mathcal{C}=\begin{pmatrix}\alpha_{1,1}&\alpha_{1,2}&\cdots&\alpha_{1,n}\\\alpha_{2,1}&\alpha_{2,2}&\cdots&\alpha_{2,n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m,1}&\alpha_{m,2}&\cdots&\alpha_{m,n}\end{pmatrix}\]으로 정의한다. 이제 식 (2)와 식 (1)을 비교해보면 임의의 $v\in V$에 대해, $L(v)$의 $\mathcal{C}$에 대한 좌표표현은 다음의 식
\[[L(v)]_\mathcal{C}=[L]^\mathcal{B}_\mathcal{C}[v]_\mathcal{B}\tag{3}\]으로 주어진다는 것을 확인할 수 있다.
그럼 정리 2에 대한 일반적인 버전은 다음의 정리로 주어진다.
정리 4 $\Hom(V,W)\cong \Mat_{m\times n}(F)$.
증명
$V$, $W$의 기저 $\mathcal{B}$, $\mathcal{C}$를 각각 고정하자. 함수 $L\mapsto[L]^\mathcal{B}_\mathcal{C}$가 linear임을 보여야 한다.
$L_1,L_2$가 모두 $\Hom(V,W)$의 원소라 하자. 그럼 각각의 $x_i\in\mathcal{B}$에 대하여,
\[\begin{aligned}L_1(x_1)&=\alpha_{1,1}y_1+\alpha_{2,1}y_2+\cdots+\alpha_{m,1}y_m\\L_1(x_2)&=\alpha_{1,2}y_1+\alpha_{2,2}y_2+\cdots+\alpha_{m,2}y_m\\&\vdots\\L_1(x_n)&=\alpha_{1,n}y_1+\alpha_{2,n}y_2+\cdots+\alpha_{m,n}y_m\end{aligned}\]그리고
\[\begin{aligned}L_2(x_1)&=\beta_{1,1}y_1+\beta_{2,1}y_2+\cdots+\beta_{m,1}y_m\\L_2(x_2)&=\beta_{1,2}y_1+\beta_{2,2}y_2+\cdots+\beta_{m,2}y_m\\&\vdots\\L_2(x_n)&=\beta_{1,n}y_1+\beta_{2,n}y_2+\cdots+\beta_{m,n}y_m\end{aligned}\]이도록 하는 스칼라들의 family $(\alpha_{i,j})$, $(\beta_{i,j})$들이 존재한다. 이제,
\[\begin{aligned}(L_1+L_2)(x_1)&=(\alpha_{1,1}+\beta_{1,1})y_1+(\alpha_{2,1}+\beta_{2,1})y_2+\cdots+(\alpha_{m,1}+\beta_{m,1})y_m\\(L_1+L_2)(x_2)&=(\alpha_{1,2}+\beta_{1,2})y_1+(\alpha_{2,2}+\beta_{2,2})y_2+\cdots+(\alpha_{m,2}+\beta_{m,2})y_m\\&\vdots\\(L_1+L_2)(x_n)&=(\alpha_{1,n}+\beta_{1,n})y_1+(\alpha_{2,n}+\beta_{2,n})y_2+\cdots+(\alpha_{m,n}+\beta_{m,n})y_m\end{aligned}\]일 것이고, 따라서 $L_1+L_2$의 행렬표현 $[L_1+L_2]^\mathcal{B}_\mathcal{C}$은 정확히 $[L_1]^\mathcal{B}_\mathcal{C}+[L_2]^\mathcal{B}_\mathcal{C}$이 된다. 이와 유사하게 스칼라곱에 대한 것도 성립한다.
정리 3 또한 비슷한 일반화를 갖는다.
정리 5 세 개의 $\mathbb{k}$-벡터공간 $V_1,V_2,V_3$와 이들 각각의 basis $\mathcal{B}_1=\{x_1,\ldots,x_n\}$, $\mathcal{B}_2=\{y_1,\ldots, y_m\}$, $\mathcal{B}_3=\{z_1,\ldots, z_k\}$가 주어졌다 하자. 그럼 임의의 $L_1:V_1\rightarrow V_2$, $L_2:V_2\rightarrow V_3$에 대하여 항상
\[[L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}=[L_2]^{\mathcal{B}_2}_{\mathcal{B}_3}[L_1]^{\mathcal{B}_1}_{\mathcal{B}_2}\]이 성립한다. 즉, linear map의 합성은 행렬의 곱과 같다.
증명
좌변의 $[L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}$을 결정하기 위해서는 $L_2\circ L_1$에 의해 $\mathcal{B}_1$의 원소들이 어디로 옮겨지는지만 확인하면 된다. $L_1$, $L_2$가 다음의 식
\[[L_1]^{\mathcal{B}_1}_{\mathcal{B}_2}=\begin{pmatrix}\alpha_{1,1}&\alpha_{1,2}&\cdots&\alpha_{1,n}\\\alpha_{2,1}&\alpha_{2,2}&\cdots&\alpha_{2,n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m,1}&\alpha_{m,2}&\cdots&\alpha_{m,n}\end{pmatrix},\quad[L_2]^{\mathcal{B}_2}_{\mathcal{B}_3}=\begin{pmatrix}\beta_{1,1}&\beta_{1,2}&\cdots&\beta_{1,m}\\\beta_{2,1}&\beta_{2,2}&\cdots&\beta_{2,m}\\\vdots&\vdots&\ddots&\vdots\\\beta_{k,1}&\beta_{k,2}&\cdots&\beta_{k,m}\end{pmatrix}\]으로 주어졌다 하자. 약간의 계산을 하면,
\[\begin{aligned}(L_2\circ L_1)(x_i)&=L_2(\alpha_{1,i}y_1+\cdots+\alpha_{m,i}y_m)\\&=\alpha_{1,i}L_2(y_1)+\alpha_{2,i}L_2(y_2)+\cdots+\alpha_{m,i}L(y_m)\\&=\alpha_{1,i}(\beta_{1,1}z_1+\beta_{2,1}z_2+\cdots+\beta_{k,1}z_k)\\&\phantom{==}+\alpha_{2,i}(\beta_{1,2}z_1+\beta_{2,2}z_2+\cdots+\beta_{k,2}z_k)\\&\phantom{===}+\cdots\\&\phantom{====}+\alpha_{m,i}(\beta_{1,m}z_1+\beta_{2,m}z_2+\cdots+\beta_{k,m}z_k)\end{aligned}\]이제, 위 식을 $z$들끼리 묶으면,
\[(L_2\circ L_1)(x_i)=\left(\sum_{l=1}^m\alpha_{l,i}\beta_{1,l}\right)z_1+\cdots+\left(\sum_{l=1}^m\alpha_{l,i}\beta_{k,l}\right)z_k\]앞서 우리는 $[L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}$의 $i$번째 열은 정확히 $x_i$가 $L_2\circ L_1$이 옮겨지는 벡터의 $\mathcal{B}_3$에서의 좌표표현이라는 것을 확인했으므로, 행렬 $[L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}$의 $i$열, $j$행은 이 벡터의 $j$번째 성분 $\sum_{l=1}^m\alpha_{l,i}\beta_{j,l}$이 된다. 앞서 정리 3에서와 마찬가지로 이 성분은 행렬곱 $[L_2]^{\mathcal{B}_2}_{\mathcal{B}_3}[L_1]^{\mathcal{B}_1}_{\mathcal{B}_2}$의 $(i,j)$번째 성분이므로 증명이 완료된다.
사실 정리 4와 정리 5를 증명하는 데에는 정리 2와 정리 3의 어떠한 결과도 사용되지 않았다. 그럼에도 불구하고 이들 정리를 별개로 서술해둔 이유는 다음 글에서 살펴본다.
기본정리의 결과들
선형대수학의 기본정리는 $V,W$에 대한 basis를 선택하기만 하면 $\Hom(V,W)$와 $\Mat_{m\times n}(F)$를 같은 것으로 취급할 수 있다는 것을 보여준다. 예컨대 $\Mat_{m\times n}(F)$의 $mn$개의 basis는 §선형사상들의 공간, ⁋명제 5에서 살펴본 $mn$개의 basis에 대응된다.
다음 따름정리 또한 기본정리의 결과이다.
따름정리 6 두 $n$차원 $\mathbb{k}$-벡터공간 $V,W$가 주어졌다 하고, 이들의 기저 $\mathcal{B},\mathcal{C}$를 고정하자. 그럼 임의의 $L\in\Hom(V,W)$에 대하여, $L^{-1}\in\Hom(W,V)$의 기저 $\mathcal{C},\mathcal{B}$에 대한 행렬표현 $[L^{-1}]^{\mathcal{C}}_{\mathcal{B}}$은 행렬 $[L]^{\mathcal{B}}_\mathcal{C}$의 역행렬과 같다.
증명
역행렬과 역함수의 유일성에 의하여 자명.
이와 같이 §행렬에서 정의한 대부분의 개념들을 $\Hom(V,W)$로 옮겨올 수 있다. 곧바로 옮겨올 수 없는 개념 중 하나는 전치행렬 $A^t$인데, 이는 다다음 글에서 쌍대공간에 대해 자세히 살펴보면 적절한 의미를 부여할 수 있다.
참고문헌
[Lee] 이인석, 선형대수와 군, 서울대학교 출판문화원, 2005.
-
미적분학의 기본정리, 대수학의 기본정리 등등과는 달리 선형대수학의 기본정리는 저자에 따라 전혀 다른 정리들을 의미하기도 한다. 예를 들어 [Goc]에서는 이전 글에서의 rank-nullity 정리를, Gilbert Strang의 경우 다음 글에서 다룰 직교여공간에 대한 정리들을 선형대수학의 기본정리라고 부른다. 우리는 [Lee]를 따라 이 정리를 선형대수학의 기본정리라 부르기로 한다. ↩

댓글남기기