이번 글에서는 사교기하에서 다루는 사교다양체가 도입된 역사적인 (물리적인) 배경을 살펴본다. 수학도로서 이곳저곳에서 주워들은 내용을 정리한 것이라 물리적으로는 오류가 조금 있을 수도 있다.
에너지 보존법칙
물리학, 특히 역학에는 물체의 운동을 서술하는 여러가지 공식이 있다. 가령 뉴턴의 운동법칙 $F=ma$는 물리학을 배우지 않은 사람이라도 모두 알고 있는 공식일 것이다.
19세기 들어 물리학자들에게 명확해진 사실 중 하나는, 이러한 공식들이 물체의 운동을 결정하는 것이 아니라 어떤 하나의 함수가 물체의 운동을 결정한다는 것이다. 어떻게 보면 이 사실은
이를 살펴보기 위해 하나의 축은 물체의 위치를, 다른 축은 물체의 운동량을 나타내는 phase space위상공간를 생각하자. 예를 들어, 1차원 공간에 해당하는 phase space는 위치 축과 운동량 축 하나씩으로 이루어진 2차원 공간이 될 것이고, 일반적으로 $n$차원 공간의 phase space는 $n$차원의 위치좌표와 $n$차원의 운동량좌표로 이루어진 $2n$차원 공간이 될 것이다.
이러한 상황에서, 운동에너지 $K=\frac{1}{2}mv^2$ 혹은 위치에너지 $P=mgh$ 등은 상수인 $m$, $g$를 제외하면 위치좌표와 속도좌표를 통해 기술할 수 있는 물리량이 된다. 즉, 이들 에너지들은 phase space에서 $\mathbb{R}$로의 함수이다. 그럼 에너지 보존법칙은 물체의 운동을 phase space에 기술하였을 때, 그 궤적은 에너지 함수의 등위면에 완전하게 포함되어야 한다는 것을 의미한다.
가령 어떠한 힘도 작용하지 않는 1차원 상에서의 물체의 운동을 생각하자. 즉, 이 물체가 가지는 에너지는 오직 운동에너지 뿐이므로, 우리는 에너지 함수 $E:\mathbb{R}^2\rightarrow\mathbb{R}$을 $E(x,v)=v^2$이라 생각할 수 있다. 그럼 $E$의 등위면은 위치축과 평행하게 그려지는 선분들이다.
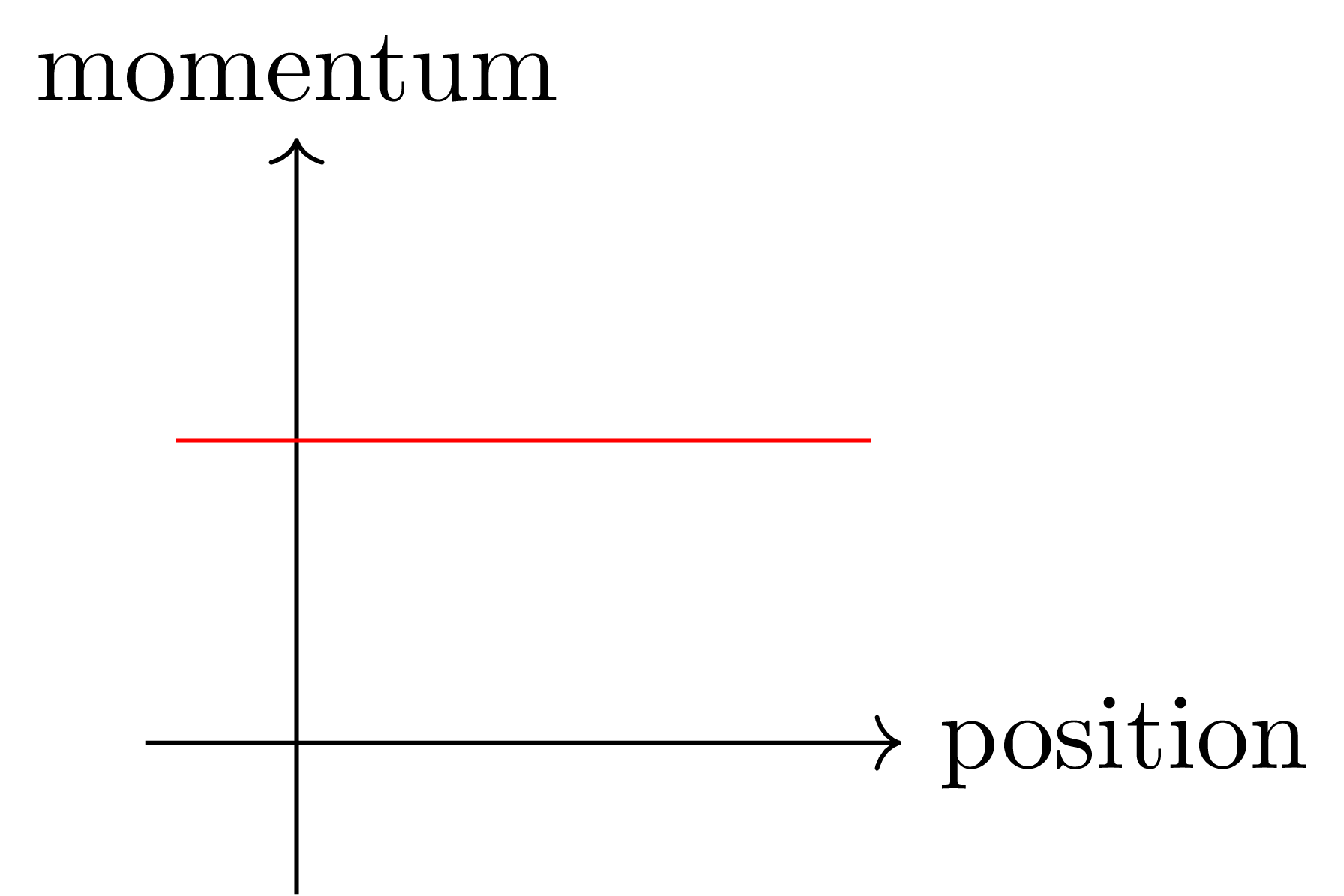
에너지 보존법칙에 의하면, 시작점이 phase space 상의 한 점인 물체는 시간이 얼마나 흐르든 이 등위면을 벗어날 수 없다. 이를 물리적으로 해석하자면, 외부의 힘이 작용하지 않을 때 물체의 가속도는 0인 것으로 해석할 수 있다.
고등학교 때 배우는 역학적 에너지 보존법칙은 일반적으로 운동에너지와 위치에너지의 합이 변하지 않는다는 것을 의미한다. 위와 비슷하게 그림을 그려보면 에너지 함수의 등위면은 대략적으로 다음과 같다.
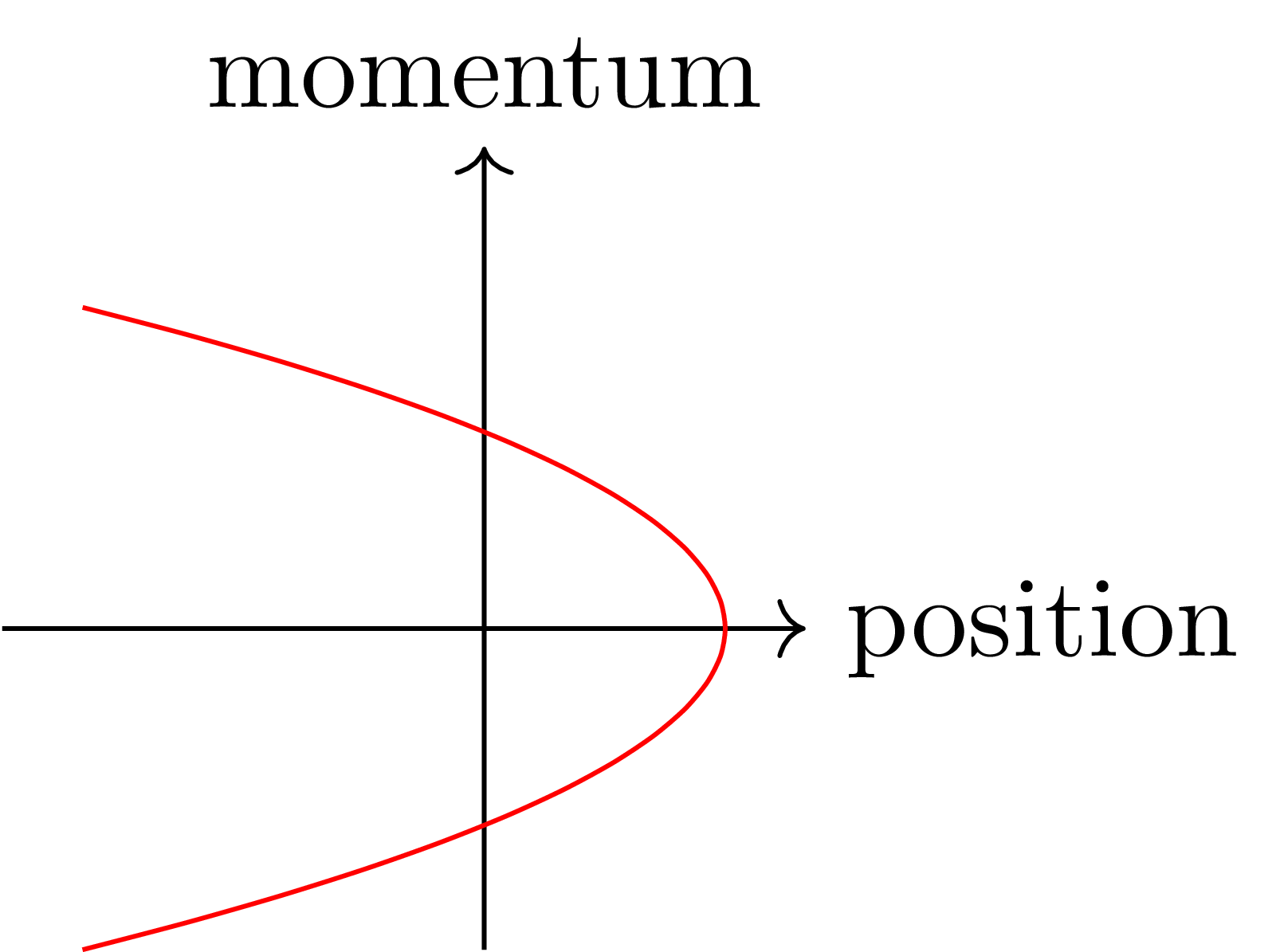
마찬가지로 에너지 보존법칙에 의하면 물체의 운동은 항상 이 에너지의 등위면 위에 있어야 한다.
마지막으로 용수철에 달린 물체의 운동을 생각하자. Hooke’s law에 따르면 용수철이 물체에 부여하는 위치에너지는 $\frac{1}{2}kx^2$으로 주어진다. 물체의 운동에너지는 $\frac{1}{2}mv^2$이므로, 에너지 함수 $E$를 $E(x,v)=\frac{1}{2}kx^2+\frac{1}{2}mv^2$으로 정의하면 된다. 이를 phase space 상에 그리면 다음과 같이 타원 형태가 나오게 된다.
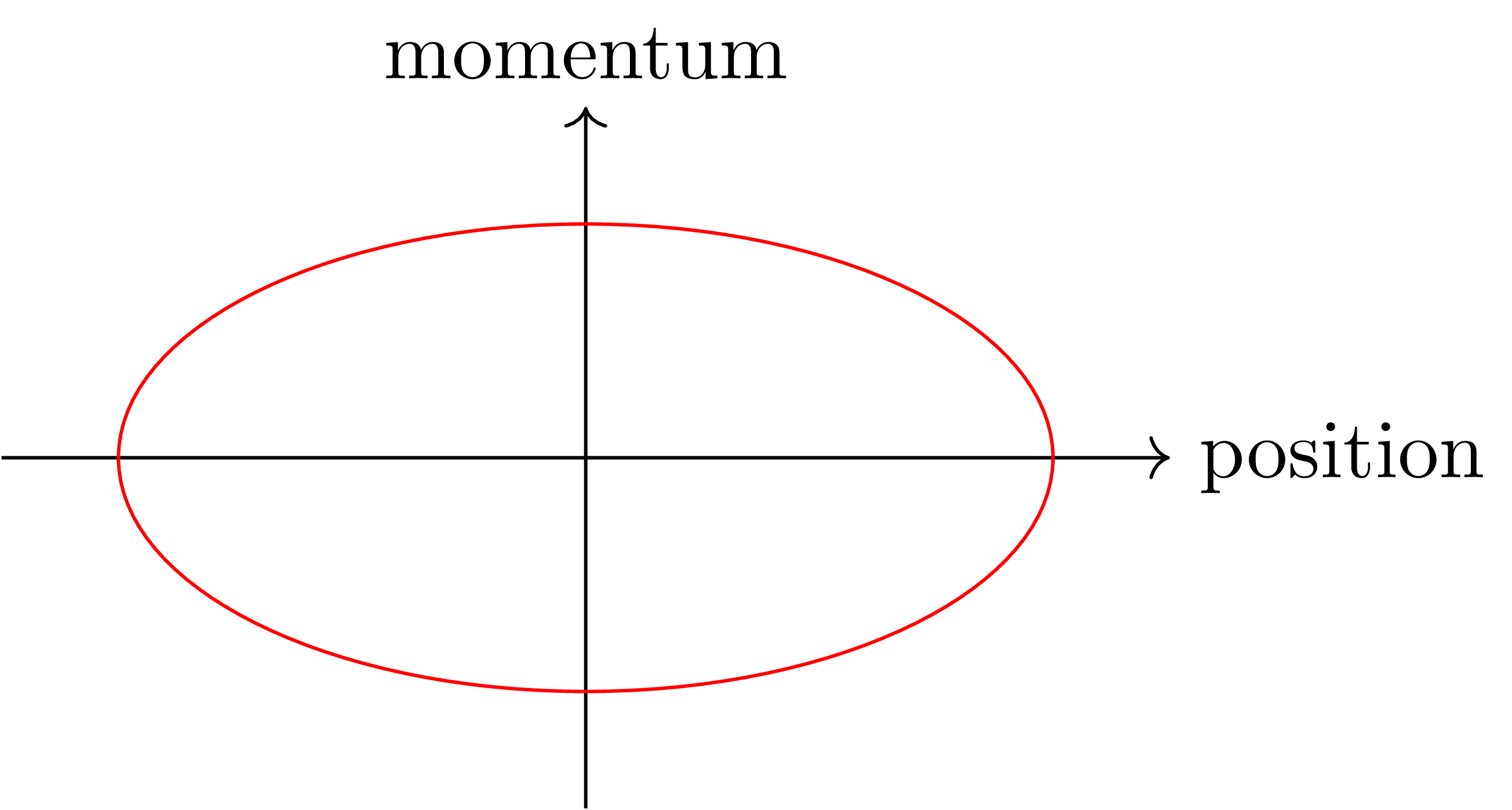
이는 물체의 운동이 주기운동이 될 것임을 암시한다.
위의 그림은 물체가 운동하는 차원이 1차원일 경우는 말이 되지만, 물체가 운동하는 차원이 2차원만 되더라도 phase space는 4차원이 되고, 따라서 에너지 등위면은 3차원이 되므로 이 안에서 물체가 실제로 어떠한 곡선을 따라 움직이는지를 설명하기 위해서는 추가적인 도구가 필요하다.
최소작용의 원리
이 과정에서 중요한 역할을 하는 것은 다음
물체가 $x_0$에서 $x_1$로 움직일 때, 이 물체는 다음의 액션의 극값 $z(t)=(x(t),y(t))$ ($t_0\leq t\leq t_1$)를 따라 움직인다.
\[\mathcal{A}_H(z)=\int_{t_0}^{t_1}\langle y,\dot{x}\rangle-H(z)\mathop{dt}\]
식에서 새로 도입한 $H$는 Hamiltonian해밀토니안을 의미하며, 앞으로 할 이야기에서는 그냥 에너지라 생각해도 무방하다. 이 원리는 $H$가 시간에 의존할 경우에도 국소적으로는 성립하며, 이 때는 $H$를 $H_t$로 바꾸어 쓰면 된다. 수학적으로 이러한 문제를 어떻게 다루는지는 아주 잘 알려져있다.
명제 1 Phase space 상의 경로 $z(t)=(x(t),y(t))$ ($t_0\leq t\leq t_1$)가 위치조건 $x(t_0)=x_0$, $x(t_1)=x_1$을 만족하는 경로들 가운데 $\mathcal{A}_H$의 극값인 것은 $z$가 다음의 Hamilton’s equation
\[\dot{x}=\frac{\partial H_t}{\partial y},\quad \dot{y}=-\frac{\partial H_t}{\partial x}\]을 만족하는 것과 동치이다.
증명
이를 증명하기 위해, 위치조건 $x_s(t_0)=x_0$, $x_s(t_1)=x_1$을 만족하는 경로들의 1-parameter family $(z_s)=(x_s,y_s)$가 주어졌다 하고, $z_0=z$라 하자. 그럼
\[\begin{aligned}\frac{\partial}{\partial s}\bigg|_{s=0}\mathcal{A}_H(z_s)&=\frac{\partial}{\partial s}\bigg|_{s=0}\int_{t_0}^{t_1}\langle y_s,\dot{x}_s\rangle-H_t(x_s,y_s)\mathop{dt}\\&=\int_{t_0}^{t_1}\frac{\partial}{\partial s}\bigg|_{s=0}\left(\langle y_s,\dot{x}_s\rangle-H_t(x_s,y_s)\right)\mathop{dt}\\&=\int_{t_0}^{t_1}\bigl\langle\partial_s y_s|_0,\dot{x}\bigr\rangle+\bigl\langle y,\partial_s\dot{x}|_0\bigr\rangle-\bigl\langle\partial_sx_s|_0,\partial_x H_t\bigr\rangle-\bigl\langle\partial_sy_s|_0,\partial_yH_t\bigr\rangle\mathop{dt}\end{aligned}\]이다. 이제 부분적분
\[\int_{t_0}^{t_1}\langle y,\partial_s\dot{x}_s|_0\rangle\mathop{dt}=\bigl[\langle y,\partial_sx_s|_0\rangle\bigr]_{t_0}^{t_1}-\int_{t_0}^{t_1}\langle\dot{y},\partial_sx_s|_0\rangle\mathop{dt}\]을 생각하면, 우변의 첫째 항은 위치조건 $x_s(t_0)=x_0$, $x_s(t_1)=x_1$으로부터 $0$이 된다. 이를 앞선 식에 대입한 후 정리하면,
\[\frac{\partial}{\partial s}\bigg|_{s=0}\mathcal{A}_H(z)=\int_{t_0}^{t_1}\langle\partial_sy_s|_0,\dot{x}-\partial_yH_t\rangle\mathop{dt}-\int_{t_0}^{t_1}\langle\partial_sx_s|_0,\dot{y}+\partial_xH_t\rangle\mathop{dt}\]이고, $\partial_sx_s|_0$과 $\partial_sy_s|_0$은 임의로 변할 수 있으므로 $z$가 $\mathcal{A}_H$의 극값이 되는 것은 두 식
\[\dot{x}-\partial_yH_t=0,\qquad\dot{y}+\partial_xH_t=0\]이 성립하는 것과 동치이다.
벡터공간 $\mathbb{R}^{2n}$에서 정의된 (linear) complex structure1 $J_0\in\End(\mathbb{R}^{2n})$을 생각하자. Basis $\{x_1,\ldots, x_n,y_1,\ldots, y_n\}$에 대하여 이 linear map은 다음의 행렬
\[J_0=\begin{pmatrix}0&-I\\I&0\end{pmatrix}\]로 주어진다. 이는 $\mathbb{R}^{2n}$을 $z_j:=x_j+iy_j$을 통하여 $\mathbb{C}^n$과 identify할 경우 허수단위 $i$와의 곱셈을 뜻한다. $\mathbb{R}^{2n}$을 manifold로, 그리고 각 점 $p\in\mathbb{R}^{2n}$마다 $T_p\mathbb{R}^{2n}\cong\mathbb{R}^{2n}$을 tangent space로 생각한다면, $J_0$은 다음의 식
\[J_0\left(\frac{\partial}{\partial x^j}\bigg|_p\right)=\frac{\partial}{\partial y^j}\bigg|_p,\qquad J_0\left(\frac{\partial}{\partial y^j}\bigg|_p\right)=-\frac{\partial}{\partial x^j}\bigg|_p\tag{1}\]으로 정의된 $\End(T\mathbb{R}^{2n})$의 원소로 생각할 수 있다. 이제
\[\nabla H=\begin{pmatrix}\partial H/\partial x\\ \partial H/\partial y\end{pmatrix}\]이므로, Hamilton’s equation은 간단하게 다음의 식
\[\dot{z}=-J_0\nabla H(z)\]으로 적을 수 있다. 직관적으로, gradient $\nabla H$는 $H$의 변화량을 가장 크게 하는 방향, 곧 $H$의 등위면에 수직인 방향을 가리키므로 $J_0$를 통해 이를 다시 90도 돌려 $H$의 등위면과 평행한 방향으로 만든 것이 $\dot{z}$인 것으로 생각할 수 있다.
따라서 phase space 상에서 물체가 실제로 운동하는 경로, 즉 $z$를 찾는 것은 다음의 Hamiltonian vector field
\[X_H=-J_0\nabla H(z)\]의 integral flow를 찾는 문제와 정확하게 같아지며, 우리는 이것이 항상 가능하다는 것을 알고 있다. ([미분다양체] §벡터장, ⁋정리 6)
Symplectic form
위의 과정을 요약하자면, 해밀토니안 $H$는 다음의 식
\[dH=\langle-J_0\nabla H(z), -\rangle\]을 통해 물체의 운동을 기술한다. 이제 $\mathbb{R}^{2n}$ 위에 $2$-form
\[\omega_0(-,-):=\langle J_0-, -\rangle\]을 정의하면, 위의 식은 함수 $f$의 gradient $f$가 $df=\langle \nabla f,-\rangle$을 정의하는 것과 유사하게
\[dH=\omega_0(X_H, -)\]으로 적을 수 있다. $\omega_0$는 $\mathbb{R}^{2n}$ 위에 정의된 canonical symplectic form이라 부르고, 이러한 관점에서 $X_H$를 symplectic gradient라고 부르기도 한다.
일반적인 $\mathbb{R}^{2n}$의 좌표계에서
\[\langle-,-\rangle=\sum_{j=1}^n dx^j\otimes dx^j+\sum_{j=1}^n dy^j\otimes dy^j\]이므로, 식 (1)을 사용하면 $\omega_0$을 각각의 basis들 $\partial/\partial x^j,\partial/\partial y^j$에서 계산할 수 있다. 예컨대
\[(\omega_0)_p\left(\frac{\partial}{\partial x^j}\bigg|_p,\frac{\partial}{\partial y^k}\bigg|_p\right)=\left\langle\frac{\partial}{\partial y^j}\bigg|_p,\frac{\partial}{\partial y^k}\bigg|_p\right\rangle_p=\delta_{jk}\]가 되며, 나머지 basis들에 대하여도 계산해보면 $\omega_0$이 standard coordinate 상에서는
\[\omega_0=\sum_{j=1}^n dx^j\wedge dy^j\]와 같이 나타난다는 것을 확인할 수 있다.
머지않아 우리는 지금까지의 논의를 임의의 manifold $M$과 cotangent bundle $T^\ast M$, Riemannian metric $g$와 almost complex structure $J$로 바꾸어도 성립한다는 것을 살펴보게 된다.
참고문헌
[MS] D. Mcduff and D. Salamon. Introduction to symplectic topology. Oxford graduate texts in mathematics. Oxford University Press, 2017.
-
벡터공간 $V$에 정의된 linear complex structure는 $J^2=-\id$를 만족하는 $J\in\End(V)$를 뜻한다. 이러한 $J$가 주어질 경우, 식 $(a+bi)\cdot v:=av+bJv$를 통해 $V$가 $\mathbb{C}$-벡터공간의 구조를 갖는다는 것을 확인할 수 있다. ↩

댓글남기기