Delta functor (작성중)

$\delta$-functor

우리는 앞서 $\mathbf{Ch}(\mathcal{C})$의 임의의 short exact sequence

\[0\longrightarrow A_\bullet\longrightarrow B_\bullet\longrightarrow C_\bullet\longrightarrow 0\]

이 주어지면, 이를 통해 long exact sequence

\[\cdots\rightarrow H_n(A)\rightarrow H_n(B)\rightarrow H_n(C)\rightarrow H_{n-1}(A)\rightarrow \cdots\]

를 만들 수 있다는 것을 증명했었다. (§호몰로지, ⁋정리 9) 이 증명의 가장 핵심적인 부분은 connecting map $\delta$를 정의하는 부분인데, 이 과정을 일반화하여 다음과 같이 정의한다.

정의 1 두 abelian category $\mathcal{A},\mathcal{B}$가 주어졌다 하자. 그럼 $\mathcal{A}$에서 $\mathcal{B}$로의 homological $\delta$-functor는 additive functor들 $T_n:\mathcal{A}\rightarrow\mathcal{B}$ ($n\geq 0$), 그리고 임의의 short exact sequence

\[0\longrightarrow A\longrightarrow B\longrightarrow C\longrightarrow 0\]

마다 정의된 morphism들 $\delta_n:T_n(C)\rightarrow T_{n-1}(A)$을 의미한다. $n<0$인 경우, $T_n$을 모두 $0$인 것으로 생각한다. 이들은 다음 조건을 만족한다.

1. (Long exact sequence) 다음의 sequence

   \[\cdots\longrightarrow T_{n+1}(C)\overset{\delta}{\longrightarrow}T_n(A)\longrightarrow T_n(B)\longrightarrow T_n(C)\overset{\delta}{\longrightarrow}T_{n-1}(A)\longrightarrow \cdots\]

   가 exact이다.

2. (Naturality) Short exact sequence들 사이의 homomorphism

   

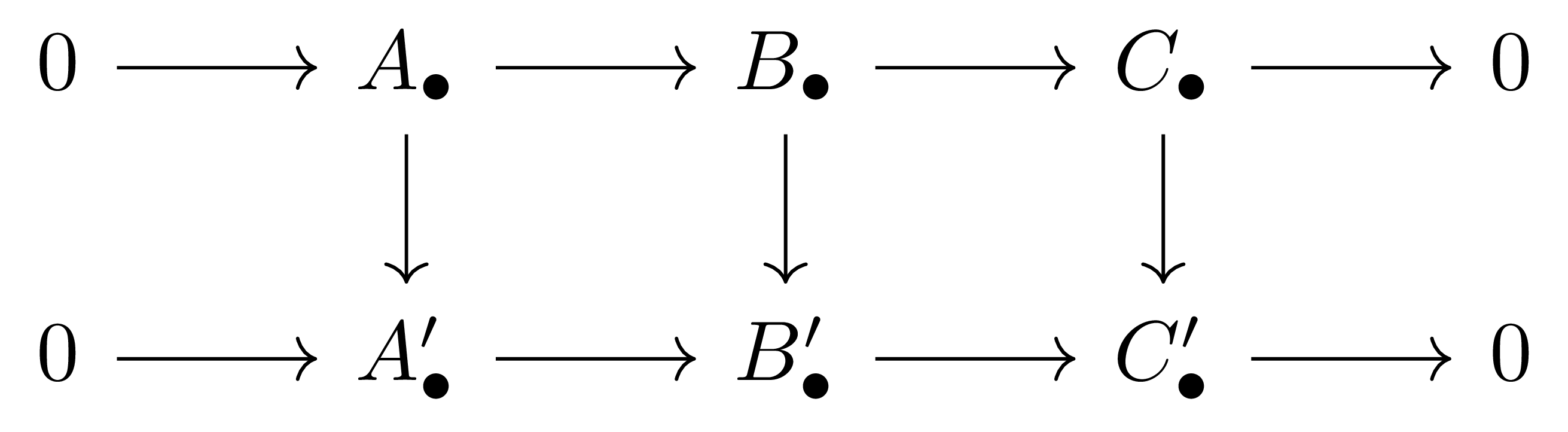
   이 주어졌을 때, 다음의 diagram

   

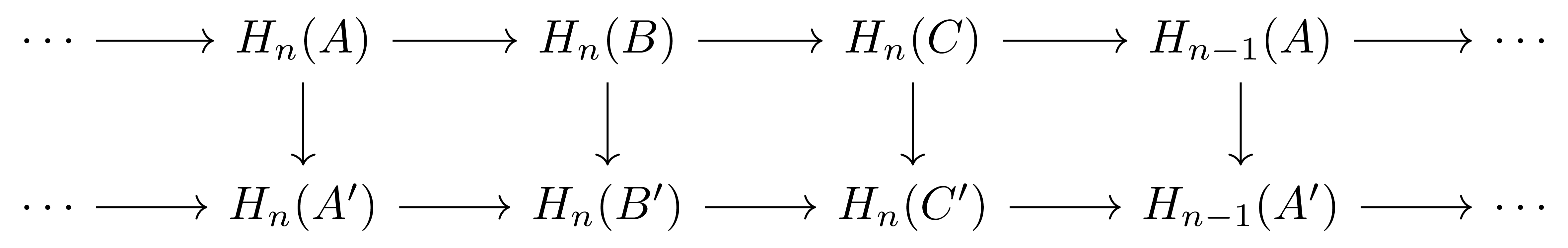
   이 commute한다.

위의 정의를 $T^n$들, 그리고 $\delta^n:T^n(C)\rightarrow T^{n+1}(A)$로 바꾸어 쓰면 cohomological $\delta$-functor의 정의를 얻는다. 우리는 $n<0$일 경우, $T_n$과 $T^n$이 모두 $0$인 것으로 생각하기로 하였으므로 homological $\delta$-functor의 첫 번째 조건은 특히

\[\cdots\longrightarrow T_0(A)\longrightarrow T_0(B)\longrightarrow T_0(C)\longrightarrow0\longrightarrow 0\longrightarrow\cdots,\]

즉 $T_0$이 right exact functor라는 의미가 된다. 마찬가지로 cohomological $\delta$-functor의 첫 번째 조건은 $T^0$이 left exact functor가 되도록 한다.

또, $\delta$-functor의 두 번째 조건인 naturality는 short exact sequence들의 모임 $\mathbf{S}(\mathcal{A})$에서 $\mathcal{A}$로 가는 두 functor $T_i(C)$와 $T_{i-1}(A)$를 생각할 때, $\delta_i$가 이들 사이의 natural transformation이 된다는 것을 의미한다.

언제나와 같이 cohomological $\delta$-functor의 경우는 homological $\delta$-functor로부터 쉽게 유도할 수 있으므로, 앞으로는 homological $\delta$-functor에 대해서만 생각하기로 한다.

정의 2 두 $\delta$-functor들 $S,T$가 주어졌다 하자. 그럼 $S$에서 $T$로의 morphism $S\rightarrow T$는 $S_n$에서 $T_n$으로의 natural transformation들의 모임들 중, $\delta$와 commute하는 것들을 의미한다.

즉 다음의 diagram이 모든 short exact sequence

\[0\longrightarrow A\longrightarrow B\longrightarrow C\longrightarrow 0\]

마다 commute하도록 하는 $\alpha_n:S_n\Rightarrow T_n$들의 모임이다.

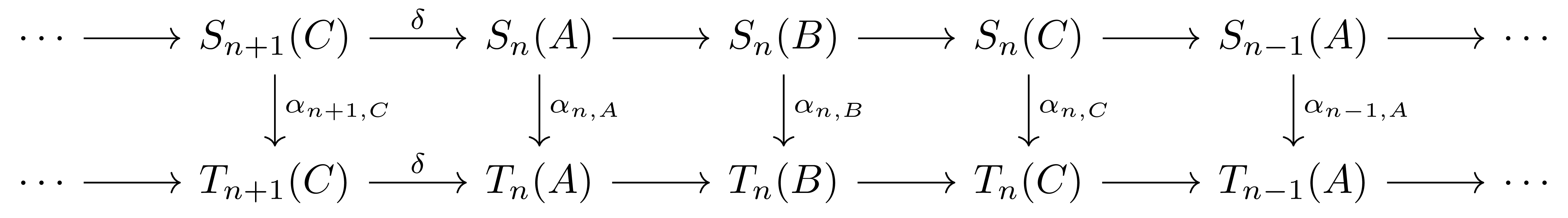
정의 3 임의의 $\delta$-functor $T$가 universal $\delta$-functor라는 것은 임의의 $\delta$-functor $S$와 natural transformation $\alpha_0:S_0\rightarrow T_0$이 주어질 때마다, 이를 확장하는 유일한 $\delta$-functor들 사이의 morphism $(\alpha_n:S_n\Rightarrow T_n)$이 존재하는 것이다.

Universal $\delta$-functor의 대표적인 예시는 derived functor인데, 이를 위해서는 projective resolution과 injective resolution을 정의해야 한다.

Projective resolution

Category $\mathbf{Mod}_R$에서, projective module은 diagram을 이용해 정의할 수 있다. 따라서 임의의 abelian category $\mathcal{A}$에서도 projective object를 정의할 수 있다.

정의 4 Abelian category $\mathcal{A}$의 object $P$가 projective object_{사영 대상}라는 것은 다음의 universal lifting property가 성립하는 것이다.

(Universal lifting property) 임의의 epimorphism $g:B\rightarrow C$와 임의의 $\gamma:P\rightarrow c$에 대하여, $\gamma=g\circ\beta$이도록 하는 $\beta:P\rightarrow B$가 존재한다.

img

다음 명제는 이미 $\mathbf{Mod}_R$에서는 익숙한 것이며, $\mathcal{A}$에서의 증명 또한 별다를 것이 없다.

명제 5 임의의 abelian category $\mathcal{A}$에 대하여, $M$이 projective인 것과 $\Hom_\mathcal{A}(M,-):\mathcal{A}\rightarrow\mathbf{Ab}$이 exact functor인 것이 동치이다.

일반적으로 abelian category $\mathcal{A}$는 projective object를 가질 수도, 갖지 않을 수도 있다. Projective resolution을 정의하기 위해서는 $\mathcal{A}$가 충분히 많은 projective object를 가져야 한다.

정의 6 Abelian category $\mathcal{A}$가 충분히 많은 projective object를 가진다는 것은 임의의 object $A\in\mathcal{A}$마다 적당한 projective object $P$와 epimorphism $P\rightarrow A$가 존재하는 것이다.

그리고 다음을 정의한다.

정의 7 Abelian category $\mathcal{A}$의 임의의 원소 $M$에 대하여, $M$의 left resolution은 다음의 exact sequence

\[\cdots\overset{d}{\longrightarrow}P_2\overset{d}{\longrightarrow}P_1\overset{d}{\longrightarrow}P_0\overset{\epsilon}{\longrightarrow}M\longrightarrow 0\]

를 의미한다. 만일 각각의 $P_i$들이 모두 projective라면 이를 projective resolution이라 부른다.

명제 8 충분히 많은 projective object를 갖는 abelian category $\mathcal{A}$의 object $M$은 항상 projective resolution을 갖는다.

증명