군의 열

교환자

우리는 [대수적 구조] §가환군, ⁋정의 3에서, 임의의 group \(G\)와 \(G\)의 두 subgroup \(H,H'\)에 대하여 이들의 commutator들로 이루어진 subgroup \([H,H']\)를 정의하였다. 해당 글에서는 \(H=H'=G\)인 경우만 생각하였으나, 이번 글에서는 이를 일반화할 것이므로 우선 commutator에 대한 성질을 더 자세히 살펴보자.

우선 \([h,h']^{-1}=[h',h]\)인 것으로부터 \([H,H']=[H',H]\)이 항상 성립한다. 만일 \([H,H']=\{e\}\)라면, 모든 \(h,h'\)에 대하여 \(hh'=h'h\)이므로 \(C_G(H)\subseteq H'\)이고 \(C_G(H')\subseteq H\)이며 이들 두 조건 중 하나가 성립하면 \([H,H']=\{e\}\)가 성립하는 것 또한 자명하다. 비슷하게, 만일 \([H,H']\subseteq H\)라 하면 임의의 \(h,h'\)에 대하여

\[h^{-1}h'^{-1}hh'\in H\implies h'^{-1}hh'^{-1}\in H\]

이므로 \(H'\subseteq N_G(H)\)이며, 마찬가지로 그 역 또한 자명하다. 마지막으로 만일 \(H,H'\)가 모두 \(G\)의 normal subgroup이었다면, \([H,H']\)의 임의의 generator \([h,h']=h^{-1}h'^{-1}hh'\)와 \(G\)의 임의의 원소 \(x\)에 대하여

\[x[h,h']x^{-1}=(xh^{-1}x^{-1})(xh'^{-1}x^{-1})(xhx^{-1})(xh'x^{-1})\]

이고, 이 때 \(H, H'\) 각각이 normal subgroup이라는 가정으로부터 \([H,H']\) 또한 \(G\)의 normal subgroup이 된다.

이러한 종류의 계산을 위한 결과를 보조정리 1에서 정리한다. 그 전에 표기법을 간단히 하기 위해, inner automorphism \(\rho_g: x\mapsto gxg^{-1}\)에 대하여

\[\rho_{g^{-1}}(x)=x^g\]

이라 적기로 하자. 그럼 [대수적 구조] §군의 작용, ⁋명제 9에 의해, 임의의 \(g_1,g_2\in G\)와 \(x\in G\)에 대하여

\[(x^{g_1})^{g_2}=x^{g_1g_2}\]

이 성립한다.

보조정리 1 임의의 \(x,y,z\in G\)에 대하여 다음이 성립한다.

1. \(xy=yx[x,y]\).
2. \(x^y=[y,x^{-1}]x\).
3. \([x,yz]=[x,z][x,y]^z=[x,z][z,[y,x]][x,y]\).
4. \([xy,z]=[x,z]^y[y,z]=[x,z][[x,z],y][y,z]\).
5. \([x^y,[y,z]][y^z,[z,x]][z^x,[x,y]]=e\).
6. \([x,yz][z,xy][y,zx]=e\).
7. \([xy,z][yz,x][zx,y]=e\).

이에 대한 증명은 단순히 각 변을 전개하는 것이므로 생략한다. 이를 사용하여 다음을 보일 수 있다.

명제 2 Group \(G\)의 세 subgroup \(H, H', H''\)에 대하여 다음이 성립한다.

1. \(H\)는 \([H,H']\)를 normalize한다.
2. 만일 \([H',H'']\)이 \(H\)을 normalize한다면, \([H,[H',H'']]\)은 \([h,[h',h]]\) 꼴의 원소들로 생성되는 \(G\)의 subgroup과 같다.

3. 만일 \(H, H', H''\)이 모두 normal이라면 다음 부등식

   \[[H, [H',H'']]\subseteq[H'',[H',H]][H', [H'',H]]\]

   이 성립한다.

증명

1. 임의의 generator \([h_1,h']\in [H,H']\)와 \(h_2\in H\)에 대하여 \([h_1,h']^{h_2}\in [H,H']\)를 보이면 충분하다. 이는 보조정리 1의 넷째 결과로부터

   \[[h_1,h']^{h_2}=[h_1h_2,h'][h_2,h']^{-1}\]

   이 성립하므로 얻어진다.

2. 편의를 위해 \([h,[h',h'']]\) 꼴의 원소들로 생성되는 \(G\)의 subgroup을 \(K\)라 하자. 그럼 \(K\subseteq [H, [H',H'']]\)인 것은 자명하므로, 우리가 보여야 할 것은 반대쪽 포함관계 \([H,[H',H'']]\subseteq K\)이다. 이제 \([H, [H',H'']]\)은 \([h, [h_1', h_1'']\cdots[h_k',h_k'']]\) 꼴의 원소들로 생성되므로 우리가 보여야 할 것은 이런 꼴의 원소들이 \(K\)에 속한다는 것이다.
   일반적으로 \(h\in H, h'\in H', h''\in H''\)와 \(x\in G\)를 고정하고 원소 \([h, [h',h'']x]\)를 생각하자. 그럼 보조정리 1의 셋째 결과로부터,

   \[[h, [h',h'']x]=[h,x][h, [h', h'']]^x=[h,x][x,[[h',h''],h]][h, [h',h'']]\]

   이 성립한다. 이제 만일 \([H',H'']\)가 \(H\)를 normalize한다는 가정으로부터 \([[h',h''],h]\)는 \(H\)의 원소이므로, 만일 \(x\)가 \([H', H'']\)의 원소였다면 위의 식의 각 항은 모두 \([H, [H',H'']]\)의 원소이다. 따라서 귀납적으로 \([H, [H',H'']]\)의 임의의 generator가 \(K\)에 속한다는 것을 보일 수 있다.

3. 마지막으로 만일 \(H, H', H''\)가 normal이라면, 셋째 결과에서 등장하는 모든 group 또한 normal subgroup이다. 따라서, 둘째 결과에 의하여 임의의 \(h,h',h''\)에 대하여 원소 \([h,[h',h'']]\)가 우변에 속한다는 것을 보이면 충분하다. 이제 \(u=h^{(h')^{-1}}\)이라 하면 다음의 식

   \[[h, [h', h'']]=[u^{h'}, [h', h'']]=[(h'')^u, [u, h']]^{-1}[(h')^{h''},[h'',u]]^{-1}\]

   으로부터 원하는 결과를 얻는다.

내림중심열과 멱영군

정의 3 Group \(G\)에 대하여, 다음의 식

\[C_1(G)=G,\qquad C_{n+1}(G)=[G, C_n(G)]\]

을 통해 \(G\)의 lower central series_{내림중심열} \((C_n(G))_{n\geq 1}\)을 정의한다.

그럼 다음이 성립한다.

명제 4 Group homomorphism \(f:G \rightarrow G'\)에 대하여, \(f(C_n(G))\subseteq C_n(G')\)이 항상 성립한다. 뿐만 아니라, 만일 \(f\)가 surjective라면 \(f(C_n(G))=C_n(G')\)이 성립한다.

증명

\(n\)에 대한 귀납법으로 진행한다. \(f(C_n(G))\subseteq C_n(G')\)라 가정하자. 그럼 \(C_{n+1}(G)\)의 원소는 정의에 의하여

\[x^{-1}y^{-1}xy,\qquad x\in G, y\in C_n(G)\]

꼴의 원소들로 생성되며,

\[f(x^{-1}y^{-1}xy)=f(x)^{-1}f(y)^{-1}f(x)f(y)\in [G, f(C_n(G))]\subseteq [G, C_n(G')]=C_{n+1}(G')\]

이므로 원하는 결과를 얻는다. 만일 \(f\)가 surjective라면, \(f(G)=G'\)이고 위의 귀납법에서 \(\subseteq\)를 \(=\)으로 대체할 수 있다.

한편, \(G\)는 \(G\)의 normal subgroup이므로, 마찬가지의 귀납법을 통해 \(C_n(G)\)들은 모두 \(G\)의 normal subgroup이며, 따라서 \(C_{n+1}(G)\)는 \(C_n(G)\)의 normal subgroup이기도 하다.

명제 5 임의의 group \(G\)와 임의의 자연수 \(m,n\)에 대하여, 다음의 포함관계

\[[C_m(G), C_n(G)]\subset C_{m+n}(G)\]

가 성립한다.

증명

명제 2의 셋째 결과로부터 우리는

\[[C_m(G), C_{n+1}(G)]=[C_m(G), [C_n(G), G]]\subseteq[G, [C_m(G), C_n(G)]][C_n(G), [G, C_m(G)]]=[G, [C_m(G), C_n(G)]][C_n(G), C_{m+1}(G)]\]

임을 안다. 따라서 만일 \([C_m(G), C_n(G)]\subseteq C_{m+n}(G)\)와 \([C_n(G), C_{m+1}(G)]\subseteq C_{m+n+1}(G)\)가 성립한다면 \([C_m(G), C_{n+1}(G)]\subseteq C_{m+n+1}(G)\)도 성립한다. 이제 임의의 \(m\)과 \(n\)에 대하여

\[[C_m(G), C_1(G)]\subseteq C_{m+1}(G),\qquad [C_1(G), C_n(G)]\subseteq C_{n+1}(G)\]

이 성립하는 것은 정의로부터 자명하므로 귀납적으로 이 부등식이 모든 \(m,n\)에 대해 성립하는 것을 안다.

이제 다음을 정의한다.

정의 6 Group \(G\)가 nilpotent group_멱영군이라는 것은 적당한 자연수 \(n\)이 존재하여 \(C_{n+1}(G)=\{e\}\)인 것이다. 이 조건을 만족하는 자연수 중 가장 큰 \(n\)을 \(G\)의 nilpotency class라 부른다.

그럼 다음이 성립한다.

명제 7 Group \(G\)와 자연수 \(n\)에 대하여, 다음이 모두 동치이다.

1. \(G\)가 nilpotent group of nilpotency class \(\leq n\)이다.

2. 적당한 \(G\)의 subgroup들의 decreasing sequence

   \[G=G_1\supset G_2\supset\cdots\supset G_{n+1}=\{e\}\]

   가 존재하여 \([G, G_k]\subseteq G_{k+1}\)이 모든 \(k\)에 대해 성립한다.

3. \(G\)의 center \(C(G)\)에 포함되어 있는 subgroup \(A\)가 존재하여, \(G/A\)가 nilpotent group of nilpotency class \(\leq n-1\)이다.

증명

우선 첫째 조건을 가정하면, \(G_k=C_k(G)\)가 둘째 조건을 만족하며, 거꾸로 둘째 조건이 성립한다면 귀납적으로 \(C_k(G)\subset G_k\)가 항상 성립하는 것을 보일 수 있다.

나머지 동치의 경우, 첫째 조건을 가정하면 셋째 조건이 성립하는 것은 \(A=C_n(G)\)로 두면 된다. 셋째 조건을 가정하고 첫째 조건이 성립하는 것을 보이는 것은 canonical morphism \(G \rightarrow G/A\)를 통해 \(C_n(G)\)를 보내면 그 image는 명제 4에 의하여 \(C_n(G/A)\)와 같고, 가정에 의해 이것이 \(\{e\}\)이므로 \(C_n(G)\subset A\)이고 따라서 \(C_{n+1}(G)=\{e\}\)임을 확인하면 된다.

따라서, 직관적으로 nilpotent group of nilpotency class \(\leq n\)은 trivial group \(\{e\}\)로부터 \(n\)개의 central extension들을 통해 얻어지는 것으로 생각할 수 있다.

명제 8 Nilpotent group \(G\) of nilpotency class \(\leq n\)과 \(G\)의 subgroup \(H\)를 고정하자. 그럼 적당한 subgroup들의 sequence

\[G=H_1\supseteq H_2\supseteq\cdots\supseteq H_{n+1}=H\]

가 존재하여 \(H_{k+1}\)이 \(H_k\)의 normal subgroup이고 \(H_k/H_{k+1}\)이 commutative이도록 할 수 있다.

증명

명제 7의 둘째 동치조건을 만족하는 \(G\)의 subgroup들의 sequence를 잡은 후, \(H_k=HG_k\)로 두면 된다.

유도열과 가해군

이제 우리는 다른 종류의 series를 정의한다.

정의 9 Group \(G\)의 derived series_유도열은 다음의 식

\[D_0(G)=G,\qquad D_{n+1}(G)=[D_n(G),D_n(G)]\]

으로 주어지는 \(G\)의 subgroup들의 series이다.

그럼 nilpotent group과 마찬가지로 다음 명제가 성립한다.

명제 10 Group homomorphism \(f:G \rightarrow G'\)에 대하여, \(f(D_n(G))\subseteq D_n(G')\)이 항상 성립한다. 뿐만 아니라, 만일 \(f\)가 surjective라면 \(f(D_n(G))=D_n(G')\)이 성립한다.

이에 대한 증명은 명제 4와 마찬가지로 귀납법을 사용하면 된다. Lower central series의 stability condition으로 nilpotent group을 정의한 것과 같이, solvable group은 derived series의 stability condition으로 정의된다.

정의 11 Group \(G\)가 solvable_가해이라는 것은 적당한 자연수 \(n\)이 존재하여 \(D_{n+1}(G)=\{e\}\)인 것이다. 이 조건을 만족하는 자연수 중 가장 큰 \(n\)을 \(G\)의 solvability class라 부른다.

정의에 의하여 \(D_0(G)=C_1(G)=G\)이고 \(D_1(G)=[G,G]=C_2(G)\)가 성립한다. 그럼 이 사실과 명제 5로부터, 귀납적으로 다음의 포함관계

\[D_n(G)\subseteq C_{2^n}(G)\]

이 성립하는 것을 안다. 즉 임의의 nilpotent group은 항상 solvable이다. 다음 명제는 명제 7에 대응되는 solvable group의 characterization이다.

명제 12 Group \(G\)와 자연수 \(n\)에 대하여, 다음이 모두 동치이다.

1. \(G\)가 solvable group of solvability class \(\leq n\)이다.

2. 적당한 \(G\)의 subgroup들의 decreasing sequence

   \[G=G_1\supset G_2\supset\cdots\supset G_{n+1}=\{e\}\]

   가 존재하여 \(G_k/G_{k+1}\)들이 모두 commutative이다.

3. \(G\)의 normal commutative subgroup \(A\)가 존재하여, \(G/A\)가 solvable group of solvability class \(\leq n-1\)이다.

따라서, 직관적으로 solvable group of solvability class \(\leq n\)은 trivial group \(\{e\}\)를 \(n\)개의 abelian group들로 extend하여 얻어지는 것으로 생각할 수 있다.

합성열과 조르단-횔더 정리

우리는 앞에서 nilpotent group들은 central extension을 반복하여 얻어지는 group이고, solvable group은 abelian extension을 반복하여 얻어지는 group인 것을 확인하였다. 이제 우리는 가장 일반적인 경우를 다룬다.

정의 13 Group \(G\)의 subgroup들의 sequence

\[G=G_0\supset G_1\supset \cdots\supset G_n=\{e\}\]

가 subnormal series_{부분정규열}이라는 것은 각 \(k\)에 \(G_{k+1}\)이 \(G_k\)의 normal subgroup인 것이며, 이 때 \(G_k/G_{k+1}\)을 이 series의 quotient라 부른다. Composition series \(G_\bullet\)보다 finer한 subnormal series가 존재하지 않는다면, 이를 \(G\)의 composition series라 부른다.

그럼 임의의 group \(G\)와 normal subgroup \(N\)에 대하여, \(G/N\)의 normal subgroup과, \(G\)의 normal subgroup 중 \(N\)을 포함하는 것들 사이의 일대일대응이 존재하므로, \(G_\bullet\)이 composition series인 것은 각각의 \(k\)에 대하여 \(G_k/G_{k+1}\)이 simple인 것과 같은 말이다. (§대칭군, ⁋정의 12)

만일 두 subnormal series

\[G=G_0\supset G_1\supset \cdots\supset G_n=\{e\},\qquad G=H_0\supset H_1\supset\cdots\supset H_m=\{e\}\]

에 대하여, \(m=n\)이고, \(G_k/G_{k+1}\cong H_{\sigma(k)}/H_{\sigma(k)+1}\)이 모든 \(k=0,\ldots, n-1\)에 대해 성립하도록 하는 \(\sigma\in S_n\)이 존재한다면 \(G_\bullet\)과 \(H_\bullet\)이 equivalent_동등한 subnormal series라 부른다. 이 절의 가장 큰 정리는 정리 16으로, group \(G\)의 두 composition series가 존재한다면 이들은 equivalent하다는 것이다. 이를 증명하기 위해 다음 보조정리부터 시작하자.

보조정리 14 (Zassenhaus) Group \(G\)의 두 subgroup \(H,K\)가 주어졌다 하고, 이들 각각의 normal subgroup \(H',K'\)가 주어졌다 하자. 그럼 \(H'(H\cap K')\)는 \(H'(H\cap K)\)의 normal subgroup이고, \(K'(K\cap H')\)는 \(K'(K\cap H)\)의 normal subgroup이며 다음의 isomorphism

\[\frac{H'(H\cap K)}{H'(H\cap K')}\cong \frac{K'(K\cap H)}{K'(K\cap H')}\]

이 존재한다.

증명

이 증명은 대략적으로 다음의 lattice

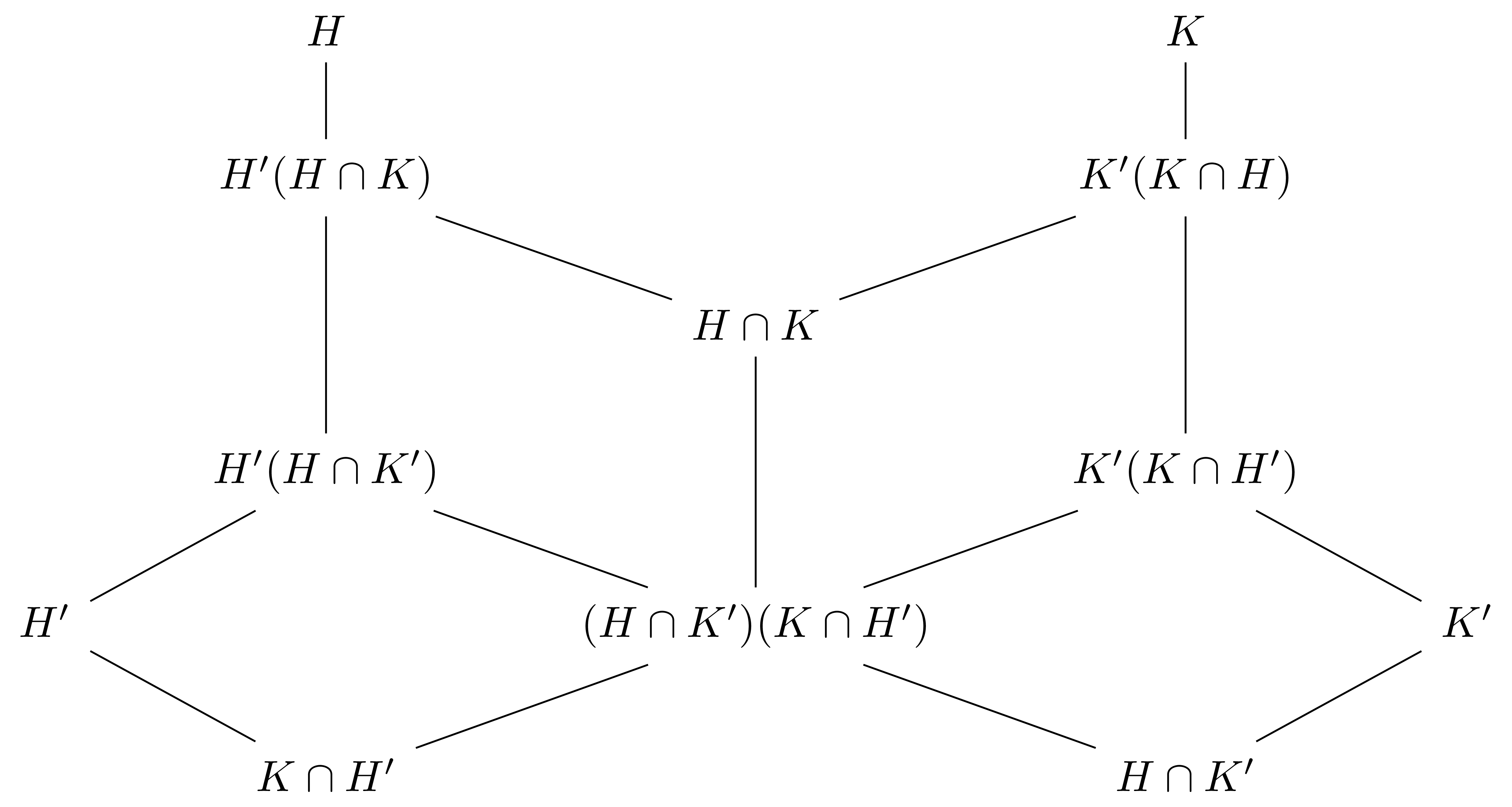
로 요약할 수 있다.

우선 \(H'\cap K=H'\cap (H\cap K)\)와 \(K'\cap H=K'\cap (K\cap H)\)가 각각 \(H\cap K\)의 normal subgroup인 것은 [대수적 구조] §군 동형사상, ⁋보조정리 4의 결과이다. 따라서 이들의 교집합인 \((H'\cap K)(K'\cap H)\) 또한 \(H\cap K\)의 normal subgroup이라는 것을 안다. 이제 주장의 isomorphism의 좌변을 보면, [대수적 구조] §군 동형사상, ⁋정리 5로부터

\[H'(H'\cap K)(K'\cap H)=H'(H\cap K')\]

이 \(H'(H\cap K)\)의 normal subgroup이고 isomorphism

\[\frac{H'(H\cap K)}{H'(H\cap K')}\cong \frac{H\cap K}{(H'\cap K)(K'\cap H)}\]

이 존재하는 것을 안다.

그럼 다음이 성립한다.

명제 15 (Schreier) 임의의 두 subnormal series

\[G=G_0\supset G_1\supset \cdots\supset G_n=\{e\},\qquad G=H_0\supset H_1\supset\cdots\supset H_m=\{e\}\]

에 대하여, 이들 각각의 refinement \(G_\bullet', H_\bullet'\)가 존재하여 이들 둘이 equivalent하도록 할 수 있다.

증명

\(G_i\)와 \(G_{i+1}\) 사이에 \(G_i\cap H_j\)를 \(j\)를 움직여 가며 넣고 \(H_j\)와 \(H_{j+1}\) 사이에 \(G_i\cap H_j\)를 \(i\)를 움직여가며 각각 끼워넣은 다음 이렇게 만들어진 refinement들이 서로 equivalent하다는 것을 보조정리 14를 통해 보일 수 있다.

따라서 다음이 성립한다.

정리 16 (Jordan-Hölder) 임의의 두 composition series는 equivalent하다.

정의 17 Group \(G\)의 length_길이는 strictly descending subnormal series의 길이의 upper bound로 정의한다.

그럼 만일 \(G\)가 composition series를 갖는다면 \(G\)의 composition series의 길이가 정확히 \(G\)의 length가 된다는 것을 안다. 따라서 다음의 등식

\[\length(G)=\length(G/N)+\length(N)\]

은 [대수적 구조] §군 동형사상, ⁋정리 7과 정리 16의 결과이다.