K

Grad. student in mathematics

카테고리의 예시들

우선 이미 존재하는 category로부터 새로운 category들을 만드는 방법을 살펴본다.

예시 1 두 category $\mathcal{A},\mathcal{B}$가 주어졌다 하자. 이들의 product category곱 카테고리 $\mathcal{A}\times \mathcal{B}$는 다음의 데이터로 이루어진다.

  • $\obj(\mathcal{A}\times \mathcal{B})$의 대상들은 쌍 $(A,B)$의 꼴이다.
  • 임의의 $(A_1,B_1),(A_2,B_2)\in\obj(\mathcal{A}\times \mathcal{B})$에 대하여, $\Hom_{\mathcal{A}\times \mathcal{B}}((A_1,B_1),(A_2,B_2))$는 $f\in\Hom_\mathcal{A}(A_1,A_2),g\in\Hom_\mathcal{B}(B_1,B_2)$에 대해 $(f,g)$의 꼴이다.
  • 임의의 $A\times B\in \mathcal{A}\times \mathcal{B}$에 대하여, $A\times B$에서의 identity는 $(\id_A,\id_B)$로 주어진다.
  • 임의의 $(f_1,g_1):(A_1,B_1)\rightarrow(A_2,B_2)$, $(f_2,g_2):(A_2,B_2)\rightarrow(A_3,B_3)$에 대해, 이들의 합성은 $(f_2\circ f_1,g_2\circ g_1)\in\Hom((A_1,B_1),(A_3,B_3))$으로 주어진다.

예시 2 Category $\mathcal{A}$가 주어졌다 하고, $A\in\obj(\mathcal{A})$를 고정하자.

  • $\mathcal{A}$의 slice category over $A$$A$ 위에서의 조각 범주 $A_{/\mathcal{A}}$는 다음과 같은 데이터로 주어진다.
    • $\mathcal{A}_{/A}$의 object들은 $\mathcal{A}$의 morphism들 $f:A_1\rightarrow A$이다.
    • 임의의 $(A_1\overset{f_1}{\longrightarrow}A)\in\obj(\mathcal{A}_{/A})$와 $(A_2\overset{f_2}{\longrightarrow}A)\in\obj(\mathcal{A}_{/A})$에 대하여, $f_1$에서 $f_2$로의 morphism은 $f_1=g\circ f_2$가 성립하도록 하는 $g:A_1\rightarrow A_2$이다.
  • $\mathcal{A}$의 slice category under $A$$A$ 위에서의 쌍대 조각 범주 ${}_{A/}\mathcal{A}$는 다음과 같은 데이터로 주어진다.
    • ${}_{A/}\mathcal{A}$의 object들은 $\mathcal{A}$의 morphism들 $f:A\rightarrow A_1$이다.
    • 임의의 $(A\overset{f_1}{\longrightarrow}A_1)\in\obj({}_{A/}\mathcal{A})$와 $(A\overset{f_2}{\longrightarrow}A_2)\in\obj({}_{A/}\mathcal{A})$에 대하여, $f_1$에서 $f_2$로의 morphism은 $f_2=g\circ f_1$가 성립하도록 하는 $g:A_1\rightarrow A_2$이다.

뭐라 썰풀지 몰루

정의 3 initial object, terminal object

위의 예시는 다음과 같이 일반화할 수 있다.

정의 4 Comma category

abelian cat. 지우기

Abelian category

이제 우리는 abelian category를 정의한다. Abelian category는 대략적으로 $\lMod{R}$과 비슷한 성질을 갖는 category로, 여기에서는 diagram chasing을 할 수 있어서 특히 유용하다. 이를 위해서는 morphism의 kernel과 image 등을 정의해야 하는데, 역시 이 또한 범주론의 언어로 쓰기 위해서는 모든 것을 대상과 morphism의 언어로 바꾸어 써야 한다. 그 후, 특정한 universal property를 만족하는 대상들로 kernel과 image를 정의한다.

Universal property를 간략히 복습하기 위해 이미 익숙한 다음 정의를 살펴보자.

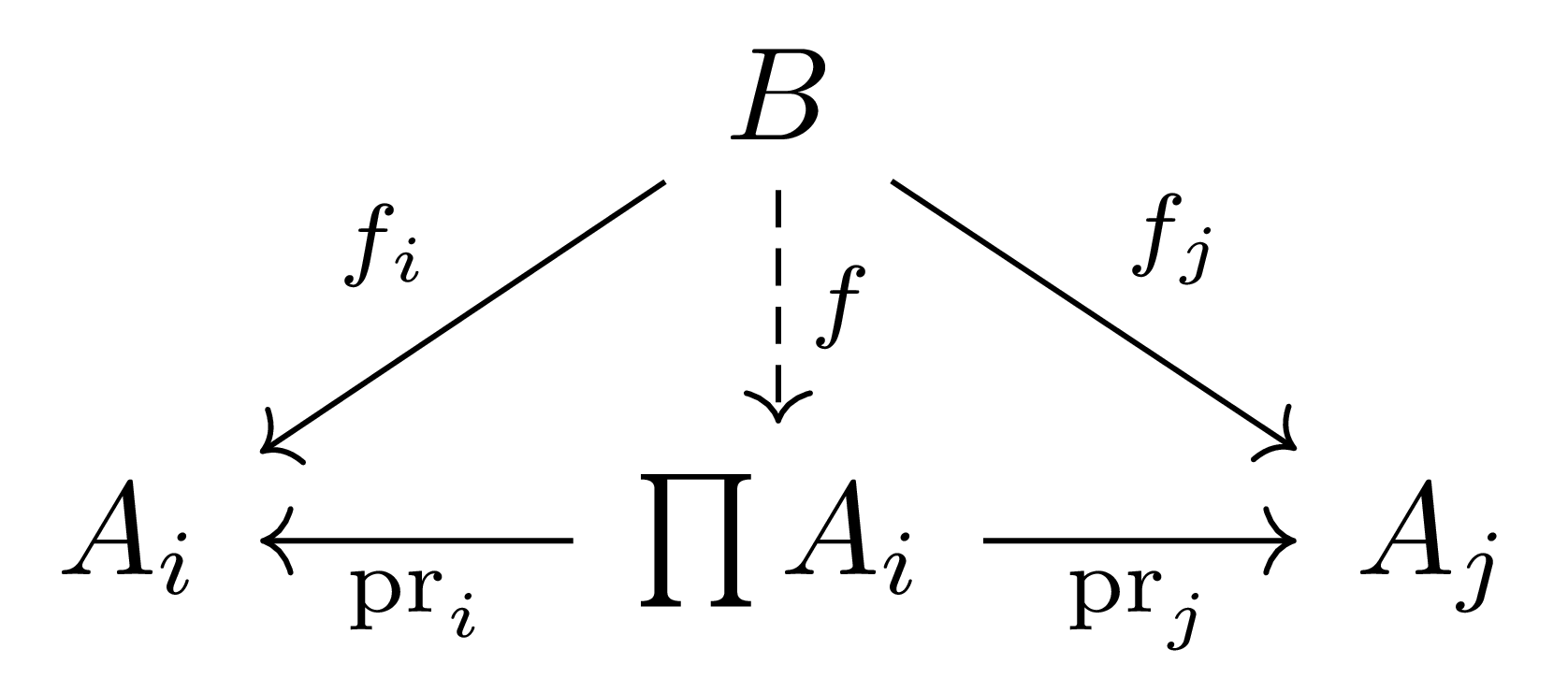
정의 3 Category $\mathcal{A}$의 대상들의 family $(A_i)_{i\in I}$에 대하여, 이들의 곱product은 다음의 universal property를 만족하는 대상 $\prod_{i\in I}A_i$과 morphism들 $(\pr_i:\prod A_i\rightarrow A_i)_{i\in I}$을 의미한다.

임의의 $B\in\obj(\mathcal{A})$와, morphism들의 family $(f_i:B\rightarrow A_i)_{i\in I}$가 주어졌다면, 다음 diagram을 commute하도록 하는 morphism $f:B\rightarrow A$가 유일하게 존재한다.

universal_property_of_product

비슷하게, 이들 family의 쌍대곱coproduct은 다음 diagram에 해당하는 universal property로 정의되는 대상과 morphism들을 의미한다.

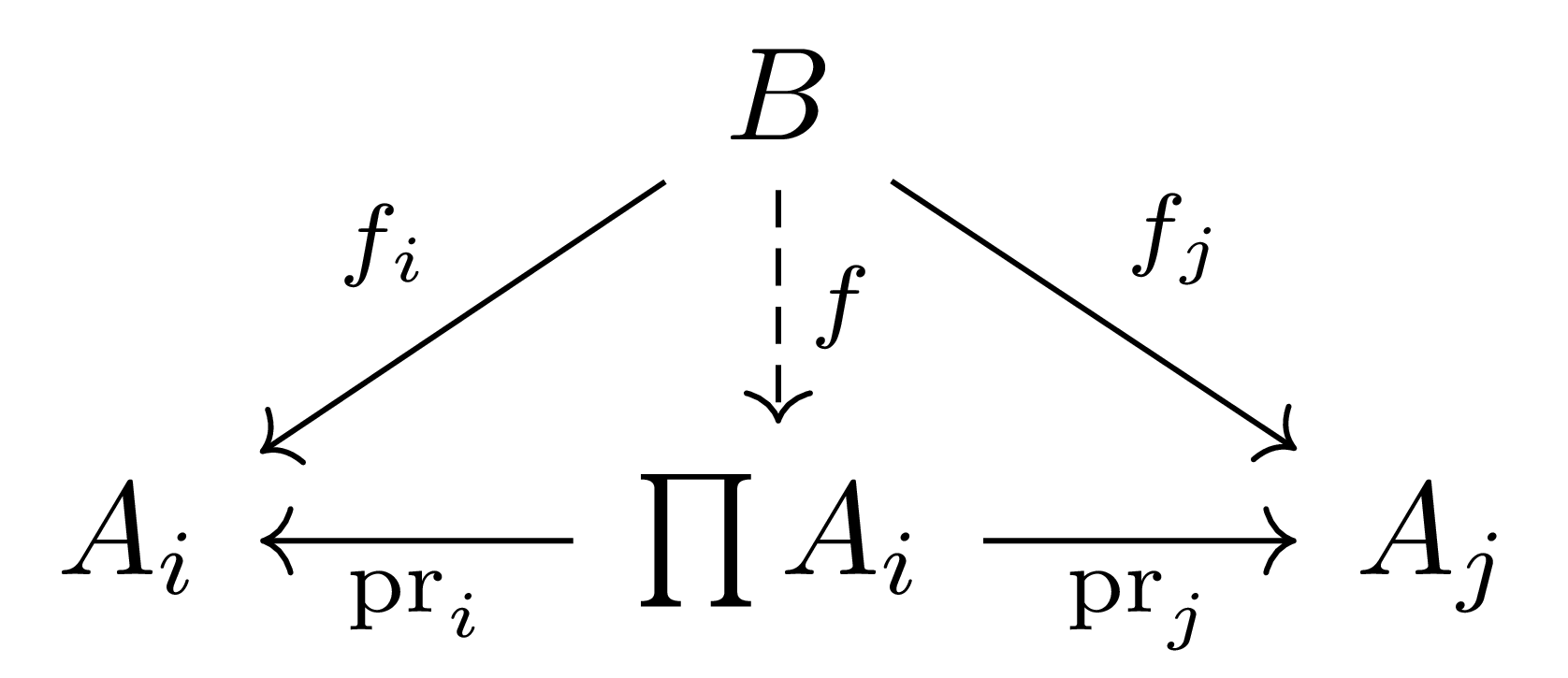
universal_property_of_coproduct

일반적인 카테고리의 일반적인 family가 product나 coproduct를 항상 가질 필요는 없지만, 만약 위의 universal property를 만족하는 쌍이 존재한다면 isomorphism에 대해 유일하게 존재한다는 것을 안다.

Kernel과 cokernel의 universal property를 살펴보기 위해서는 우선 $0$이 무엇인지부터 정의해야 한다.

정의 4 Category $\mathcal{A}$를 생각하자.

  • 대상 $I$가 initial시작 대상이라는 것은 임의의 $A\in\obj(\mathcal{A})$에 대하여, 유일한 $I\rightarrow A$가 반드시 존재하는 것이다.
  • 대상 $T$가 terminal끝 대상이라는 것은 임의의 $A\in\obj(\mathcal{A})$에 대하여, 유일한 $A\rightarrow T$가 반드시 존재하는 것이다.
  • 어떠한 대상 $Z\in\obj(\mathcal{A})$가 initial인 동시에 terminal이라면, $Z$를 zero object영 대상라 부른다.

$\mathbf{Set}$은 initial object를 갖지 않고, 따라서 zero object도 갖지 않는다. 한편 $\mathbf{Group}$에서는 trivial group $\{e\}$가 zero object가 되고, $\lMod{R}$에서는 zero module $0$이 zero object가 된다.

카테고리 $\mathcal{A}$가 zero object를 갖는다고 하자. 그럼 임의의 $A,B\in\obj(\mathcal{A})$에 대하여 $A\rightarrow 0$과 $0\rightarrow B$가 유일하게 결정되며 따라서 $\Hom_\mathcal{A}(A,B)$에는 이들의 합성 $0_{AB}:A\rightarrow 0\rightarrow B$가 존재한다. 이를 zero map영 사상이라 부른다.

이제 $0$을 정의하였으므로, kernel과 cokernel을 정의할 수 있다.

정의 5 Zero object를 갖는 category $\mathcal{A}$의 두 대상 $A,B$ 사이의 morphism $f:A\rightarrow B$를 생각하자.

  • Morphism $i:K\rightarrow A$가 $f$의 kernel핵이라는 것은 $f\circ i=0$이며, 다음의 universal property를 만족하는 것이다.

    임의의 $j:Z\rightarrow A$가 $f\circ j=0$을 만족한다면, 다음 diagram을 commute하도록 하는 유일한 morphism $Z\rightarrow K$가 항상 존재한다.

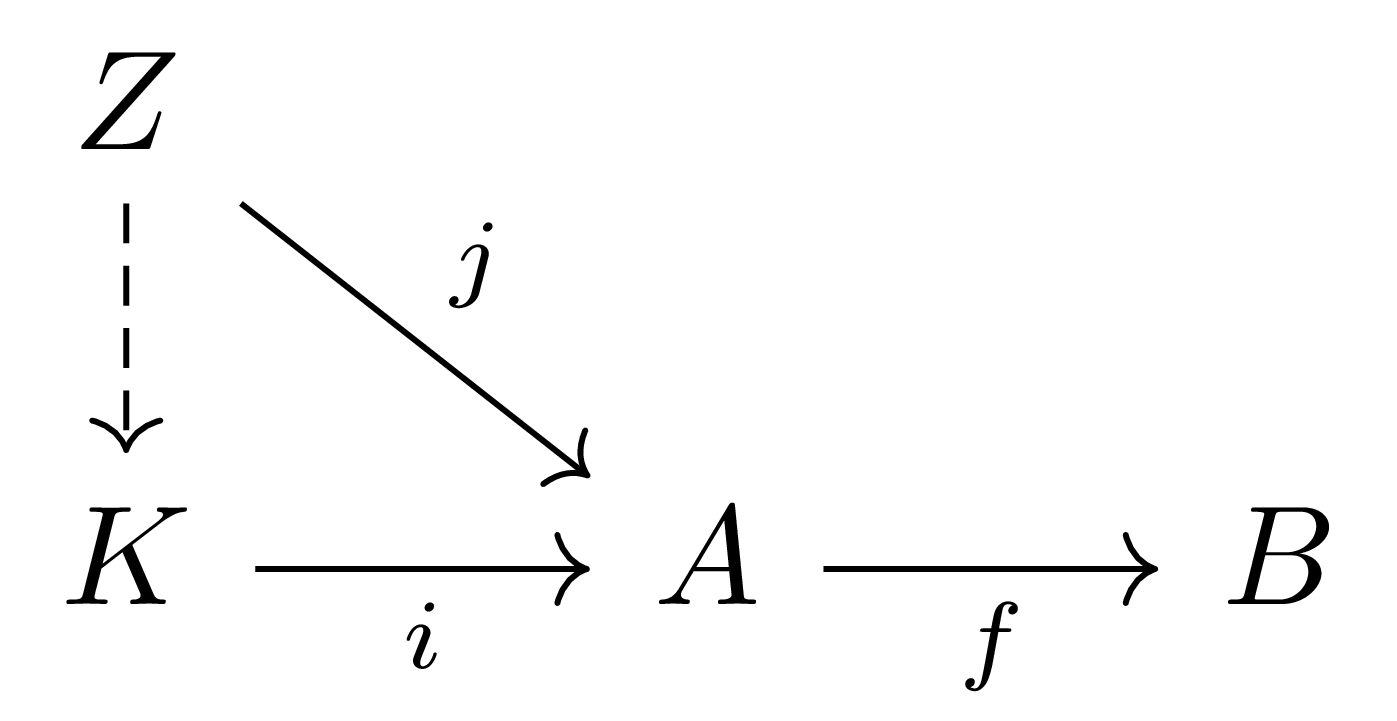
    universal_property_of_kernel

  • 비슷하게, $f$의 cokernel여핵은 다음 diagram에 해당하는 universal property를 만족하는 morphism $p:B\rightarrow C$로 정의된다.

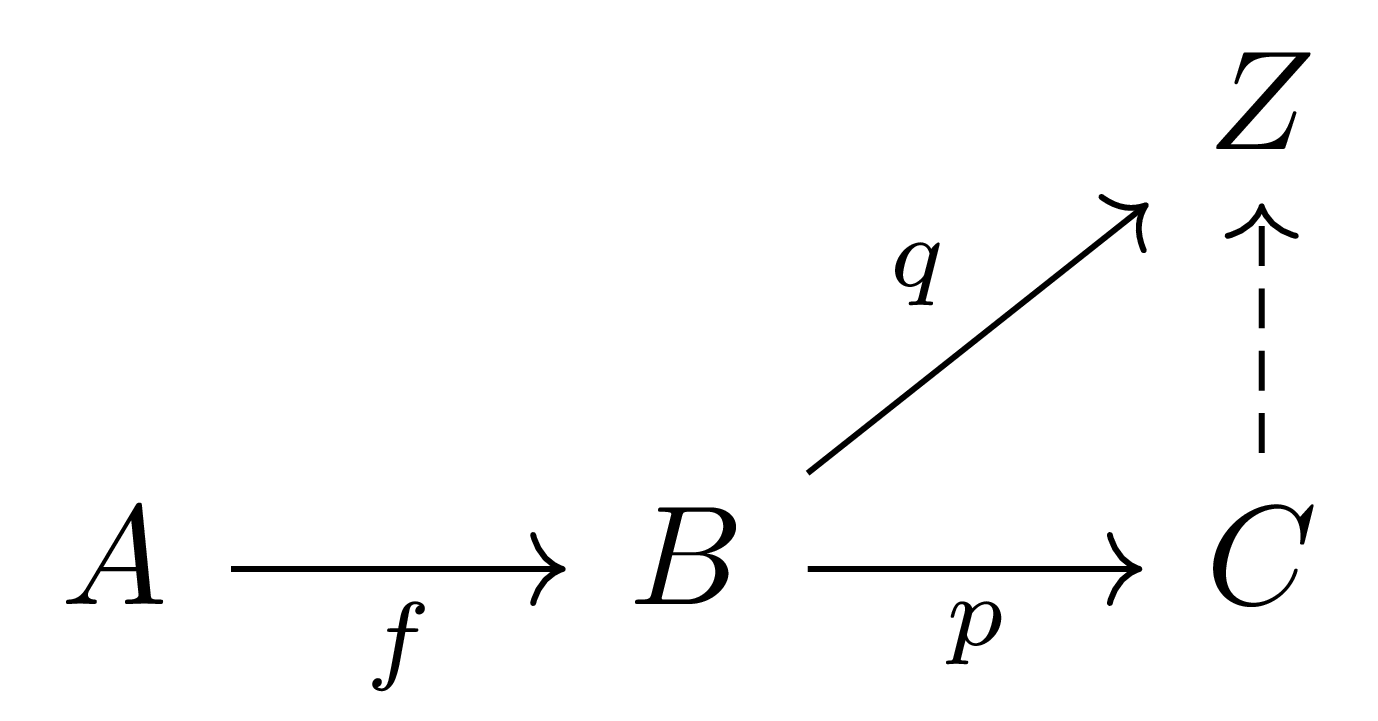
universal_property_of_cokernel

정의에 의하여 kernel은 항상 monomorphism이고 cokernel은 항상 epimorphism이 된다. §카테고리, ⁋예시 2에서 살펴본 대수적 구조들에서 $\Hom(A,B)$들은 단순한 집합이 아니라 그 위에 다음의 연산

\[(f\star g)(a)=f(a)\star g(a)\qquad\text{for all $a\in A$}\]

이 정의된 또 다른 대수적 구조이다. 특히 원래 category의 대상들이 abelian group의 구조를 갖고 있었다면 위의 연산을 통해 $\Hom(A,B)$ 또한 abelian group의 구조를 갖는다.

정의 6 Category $\mathcal{A}$가 $\Ab$-category라는 것은 $\Mor_\mathcal{C}(A,B)$가 모두 abelian group의 구조를 갖고 있으며, 이 때 $(\Mor_\mathcal{C}(A,B),+)$가 합성에 대한 분배법칙을 만족하는 것이다. 즉, 임의의 $g_1,g_2\in\Mor_\mathcal{C}(B,C)$와, 임의의 $f:A\rightarrow B$ 혹은 $h:C\rightarrow D$에 대하여

\[(g_1+g_2)\circ f=g_1\circ f+g_2\circ f,\qquad h\circ(g_1+g_2)=h\circ g_1+h\circ g_2\]

이 모두 성립하는 것이다.

정의 7 $\Ab$-category $\mathcal{A}$가 additive category덧셈 카테고리라는 것은 $\mathcal{A}$가 zero object를 가지고, 임의의 $A,B\in\obj(\mathcal{A})$에 대하여 그 곱 $A\times B$가 항상 존재하는 것이다.

두 additive category $\mathcal{A},\mathcal{B}$ 사이의 functor $F:\mathcal{A}\rightarrow\mathcal{B}$가 additive functor덧셈함자라는 것은 $F$가 abelian group $\Hom_\mathcal{A}(A,B)$에서 $\Hom_\mathcal{B}(FA,FB)$ 사이의 group homomorphism을 유도하는 것이다.

Additive category에서는 임의의 $A,B\in\obj(\mathcal{A})$에 대하여, zero map영사상 $0_{AB}:A\rightarrow B$가 $A\rightarrow 0\rightarrow B$로 정의된다. 이렇게 정의한 zero map은 물론 abelian group $\Hom_\mathcal{A}(A,B)$의 덧셈에 대한 항등원이 된다.

명제 8 임의의 additive category $\mathcal{A}$와 두 대상 $A,B\in\obj(\mathcal{A})$에 대하여, 위에서 정의한 zero map $0_{AB}$는 $\Hom_\mathcal{A}(A,B)$의 덧셈에 대한 항등원이다.

증명

Zero object $0$에서 $B$로의 morphism $0_{0B}$가 유일하게 존재한다. 따라서 $0_{0B}+0_{0B}=0_{0B}$가 성립한다. 이제 주어진 명제는 다음의 식

\[0_{AB}+0_{AB}=0_{0B}\circ0_{A0}+0_{0B}\circ0_{A0}=(0_{0B}+0_{0B})\circ 0_{A0}=0_{0B}\circ 0_{A0}=0_{AB}\]

으로부터 자명하다.

이제 abelian category를 정의할 수 있다.

정의 9 Additive category $\mathcal{A}$가 abelian category아벨 카테고리라는 것은 다음 조건들이 추가로 성립하는 것이다.

  1. 임의의 homomorphism이 kernel과 cokernel을 갖는다.
  2. 임의의 monomorphism $f$는 $\coker f$의 kernel과 같다.
  3. 임의의 epimorphism $f$는 $\ker f$의 cokernel과 같다.

Abelian category에서는 임의의 homomorphism $f:A\rightarrow B$에 대해 $f$의 kernel $i:\ker f\rightarrow A$와 cokernel $p:B\rightarrow \coker f$가 존재한다. 직관적으로 $\lMod{R}$에서 살펴보면, $i:\ker f\rightarrow A$는 $A$의 submodule $\ker f$의 $A$로의 canonical inclusion으로 생각할 수 있고, cokernel $p:B\rightarrow \coker f$는 canonical projection으로 생각할 수 있다.

임의의 abelian category $\mathcal{A}$에서, $f$의 image는 다음의 morphism

\[\ker(\coker f)\rightarrow\coker f\]

으로 정의된다. 이를 $\lMod{R}$에서 살펴보면 $f$의 cokernel은 canonical projection $p:B\rightarrow B/\im f$이고, 따라서 $\ker p=\ker(\coker f)$는 $\lMod{R}$에서 우리가 알고 있는 image의 개념과 잘 맞아떨어진다. 비슷하게, $f$의 coimage는 다음의 morphism

\[\coim(f)=\coker(\ker(f))\]

으로 정의한다.

일반적인 abelian category에서, monomorphism $f:A\rightarrow B$가 주어진다면 $\coker f$를 quotient object라 부르고 $B\rightarrow B/A$, 혹은 더 간단히 $B/A$라 표기한다. 이 또한 $\lMod{R}$에서는 자명한 것이다.

예시 10 (Homology) Abelian category $\mathcal{A}$에서는 kernel과 image가 잘 정의되며, 이들의 quotient object로 호몰로지를 정의할 수 있고, 이것이 $0$이 된다는 것이 exactness이므로 $\mathcal{A}$에서 short exact sequence 또한 잘 정의된다. 즉 abelian category에서는 “diagram chasing”을 할 수 있다. 예컨대

\[C_{n+1}\overset{d_{n+1}}{\longrightarrow} C_n\overset{d_n}{\longrightarrow} C_{n-1}\]

이 $d_{n+1}\circ d_n=0$을 만족한다면, 다음의 diagram

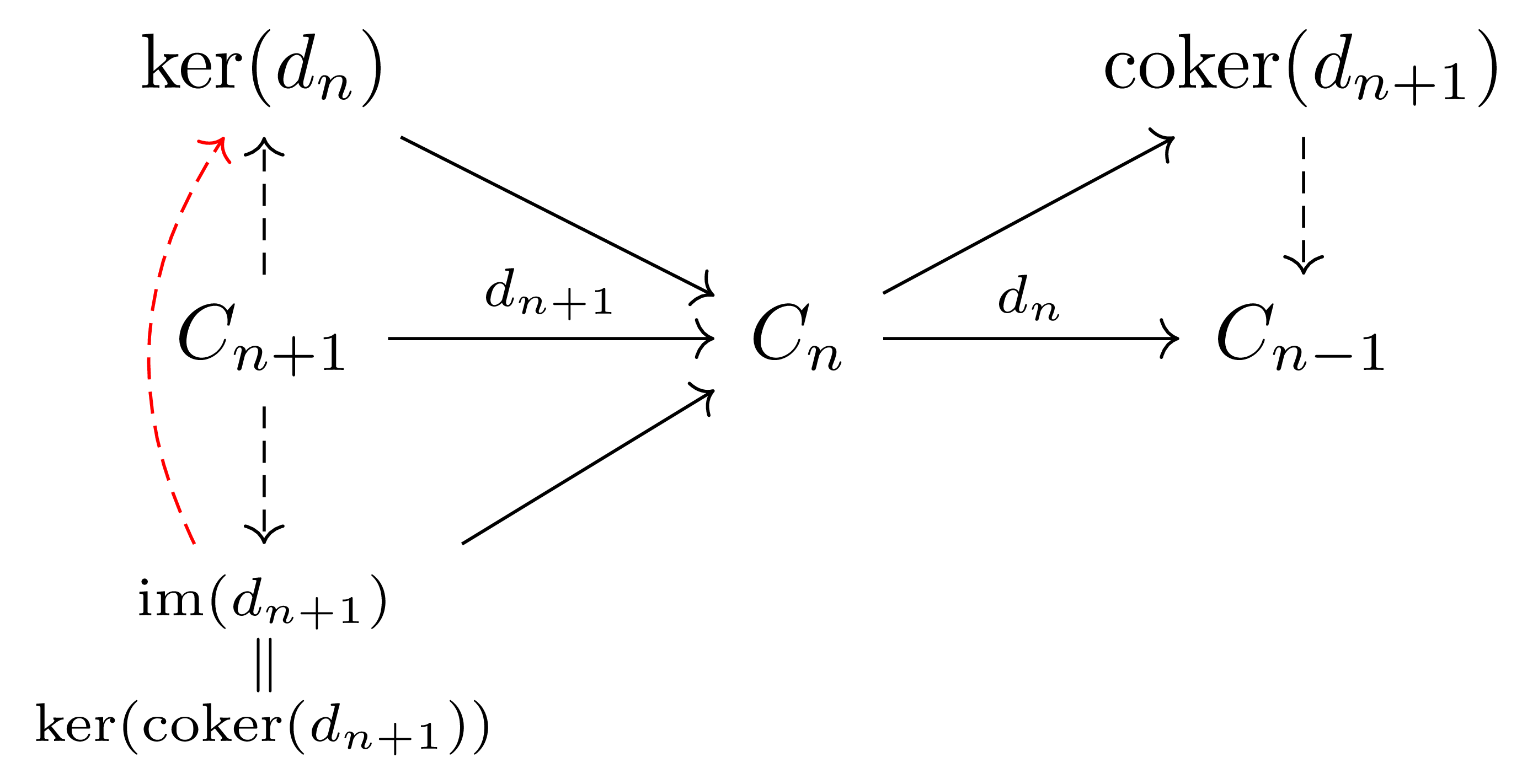
homology_in_abelilan_category

을 따라 monomorphism $\im(d_{n+1})\rightarrow\ker(d_n)$을 정의할 수 있으며, 따라서 quotient $H_n(C)=\ker(d_n)/\im(d_{n+1})$이 잘 정의된다. 이 때 위의 chain complex가 $C_n$에서 exact라는 것은 $H_n(C)=0$인 것이다.

앞서 살펴본 것처럼 abelian category에서는 kernel, cokernel, image와 quotient 등이 모두 정의된다. 이로부터 $\lMod{R}$에서의 정리들이 모두 성립한다. 가령 first isomorphism theorem을 임의의 abelian category의 언어로 바꾸어 쓰자면,

임의의 abelian category $\mathcal{A}$의 morphism $f:A\rightarrow B$가 주어졌다 하자. 그럼 $A/\ker f\cong \im f$가 성립한다.

와 같이 적을 수 있으며, 좌변은 $i:\ker f\rightarrow A$로부터 얻어지는 quotient object가 된다. 이러한 종류의 정리들은 모두 abelian category로 올릴 수 있고, 증명 또한 kernel과 cokernel의 universal property 등만 이용하여 진행할 수 있으나 그 증명은 다소 복잡하다.

따라서, 일반적으로는 이러한 정리들을 일일히 보이는 대신 다음 정리를 사용한다.

정리 11 (Freyd-Mitchell embedding theorem) 임의의 small abelian category $\mathcal{A}$에 대하여, 적당한 ring $R$과 fully faithful, exact functor $F:\mathcal{A}\rightarrow\lMod{R}$이 존재한다.

여기에서 functor $F$가 exact라는 것은 $\mathcal{A}$의 short exact sequence가 $\lMod{R}$의 short exact sequence로 옮겨진다는 것이다.

참고문헌

[Rie] Emily Riehl. Category Theory in Context. Dover Publications, 2016.
[Wei] C.A. Weibel. An Introduction to Homological Algebra. Cambridge Studies in Advanced Mathematics. Cambridge University Press, 1995.
[Vak] R. Vakil, The rising sea: foundations of algebraic geometry. 2015. Preprint. 링크

댓글남기기