일반적으로 그 구조가 복잡한 수학적인 대상을 다룰 때 좋은 전략 중 하나는 이 대상이 다른 단순한 대상 위에 어떻게 작용하는지를 보는 것이다. 이 카테고리에서 우리는 표현론, 그 중에서도 finite group의 표현론에 대해 살펴본다.
표현론의 기본 개념들
우선 다음의 정의부터 시작하자.
정의 1 임의의 finite group $G$에 대하여, $G$의 representation표현은 유한차원 벡터공간 $V$와, group action의 조건을 만족하는 함수
\[\rho: G\times V \rightarrow V\]가 주어져서 각각의 $\rho(g,-)$가 linear map인 것이다.
일반적으로 ground field $\mathbb{K}$는 임의의 ring $A$로 대체해도 아무런 문제는 없지만, 우리의 논의에서는 $\mathbb{K}=\mathbb{C}$로 두어도 충분하므로 이렇게 고정하기로 한다. 또, 우리는 주로 유한차원 벡터공간 $V$를 representation space로 갖는 경우를 생각하고 있음을 기억하자. 이 또한 무한차원 벡터공간으로 일반화할 수 있지만, 이를 위해서는 $V$에 topological vector space 구조를 주는 등의 표준적인 방법들이 필요하다.
위의 정의는 간략하게 $G\rightarrow\Aut(V)$가 주어진 것으로 생각할 수 있다. 우리는 약간의 abuse of notation을 통해 $\rho(g,-): V\rightarrow V$를 간단히 $\rho(g)\in \Aut(V)$로 쓰기도 하고, 더욱 표기를 생략하여 $\rho(g)v$ 대신 $g\cdot v$와 같이 쓰기도 한다. 이 표기에서 알 수 있듯, 우리는 $V$를 $G$-module처럼 생각하며, 이러한 관점에서 (스칼라곱은 암묵적으로 주어졌다고 하고) $V$를 $G$의 representation이라 간단히 말하기도 한다.
Finite group $G$를 고정하고, 두 representation $V,W$가 주어졌다 하자. 그럼 $V$에서 $W$의 morphism은 다음의 diagram
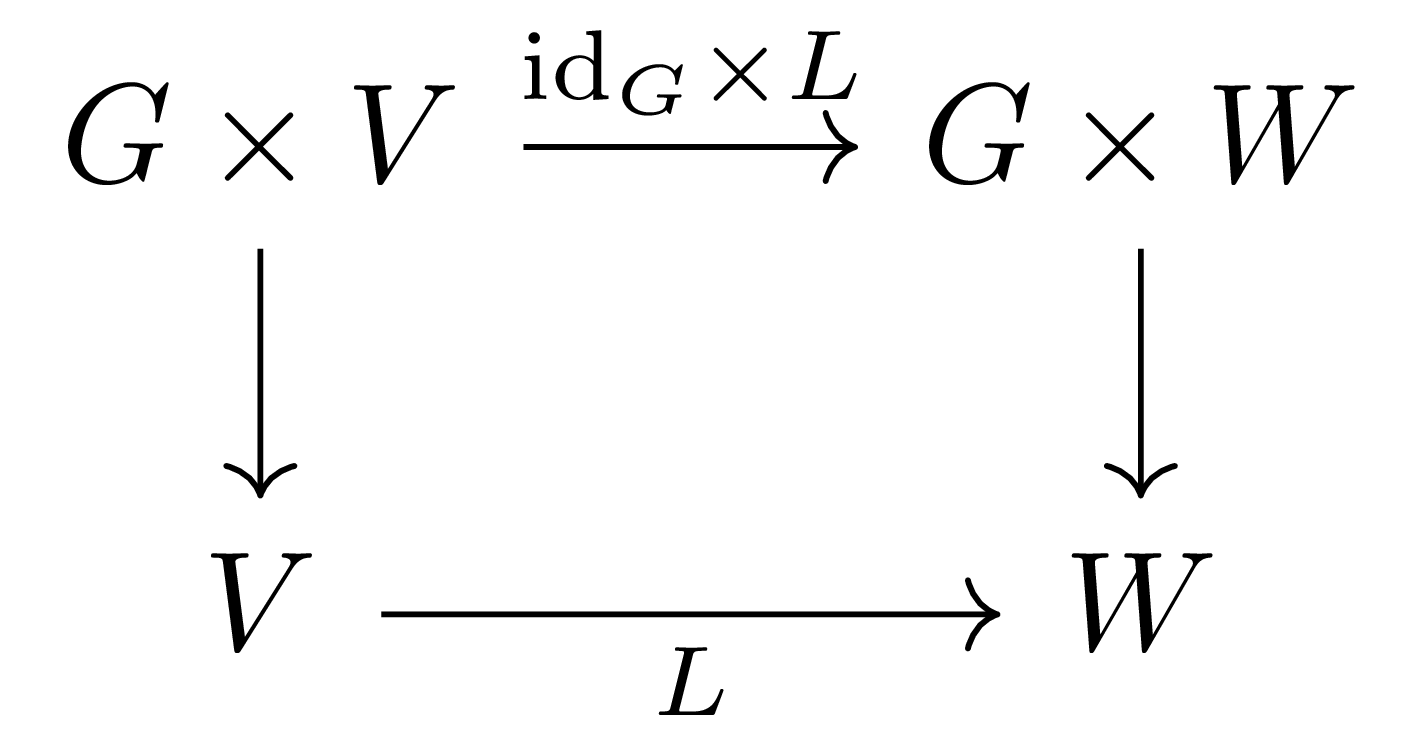
으로 주어진다. 이는, 식으로 표현하면, 간단히
\[L(g\cdot v)=g\cdot L(v)\qquad\text{for all $g\in G$ and $v\in V$}\]으로 적을 수 있다.
한편 $V$에 적용되는 선형대수학의 언어를 차용하면 다음을 정의할 수 있다.
정의 2 Group $G$의 representation $G\times V\rightarrow V$에 대하여 다음을 정의한다.
- $V$의 subspace $W$가 $G$-invariant$G$-불변공간라는 것은 임의의 $g\in G$와 임의의 $w\in W$에 대하여 $g\cdot w\in W$가 항상 성립하는 것이다.
- 임의의 $G$-invariant subspace $W$에 대하여, representation $G\times W\rightarrow W$를 $V$의 subrepresentation부분표현이라 부른다.
- 만일 $V$가 zero representation이 아니고 $V$의 subrepresentation들이 trivial subrepresentation들, 즉 자기 자신과 $G\times\{0\}\rightarrow\{0\}$ 뿐이라면 $V$를 irreducible representation기약표현이라 부른다.
이와 마찬가지 관점에서 우리는 임의의 representation $V,W$에 대하여, 이들의 벡터공간에서의 연산을 이용하여 $V\oplus W$, $V\otimes W$ 등을 정의할 수 있다. 다음 정의에서 다소 주의할 것은, 위의 정의 2와는 다르게 $V\otimes W$ 등에서는
정의 3 $G$-representation $V, W$에 대하여, 다음의 $G$-action을 통해 새로운 $G$-representation들을 정의한다.
- Direct sum $V\oplus W$; $G$-action $g\cdot(v,w)=(g\cdot v,g\cdot w)$
- Tensor product $V\otimes W$; $G$-action $g\cdot(v\otimes w)=(g\cdot v)\otimes (g\cdot w)$, 그리고 이로부터 얻어지는 exterior power $\bigwedge^k V$, symmetric power $\operatorname{Sym}^k V$와 그 위의 $G$-action들
- $\Hom_\mathbb{C}(V,W)$; $G$-action $(g\cdot f)(v)=g\cdot f(g^{-1}\cdot v)$
- 3번에서 $W=\mathbb{C}$로 두어 얻어지는 dual representation $V^\ast$
- 스칼라곱을 conjugate으로 바꾸어 얻어지는 conjugate representation $\overline{V}$ (동일한 $G$-action)
Category $\lMod{\mathbb{C}[G]}$
위의 [정의 3]에서 tensor product와 $\Hom$의 경우 다소 그 정의가 인위적으로 보일 수 있는데, 이를 탐구하기 위해서는 group algebra의 언어가 유용하다. ([대수적 구조] §대수, ⁋정의 5) 이를 간단히 리뷰하자면, 집합으로서 $\mathbb{C}[G]$는 $G$에서 $\mathbb{C}$로의 함수들의 모임이었다. 각각의 $x\in G$에 대하여 $\delta_x:G\rightarrow \mathbb{C}$를
\[\delta_x(y)=\begin{cases}1&\text{if $y=x$}\\0&\text{otherwise}\end{cases}\]으로 정의하면, 임의의 $\varphi\in\mathbb{C}[G]$는
\[\phi=\sum_{x\in G}\phi(x)\delta_x\]로 나타낼 수 있으므로 $\delta_x$들이 $\mathbb{C}[G]$의 basis를 이룬다. 우리가 다룰 $\mathbb{C}[G]$가 단순히 $G$에서 $\mathbb{C}$로의 함수들이 이루는 ring과 같지 않은 부분은 이 위에 정의된 곱셈이다. 두 함수 $\phi,\psi$의 곱셈을
\[(\phi\psi)(x)=\phi(x)\psi(x), \qquad \text{for all $x\in G$}\]으로 정의하는 대신 이 위에는 convolution product
\[(\phi\ast \psi)(x)=\sum_{y\in G}\phi(y)\psi(y^{-1}x)\]가 곱셈을 정의한다. 만일 우리가 위의 delta function $\delta_x$와 $x\in G$를 identify한다면, 다음의 식
\[\left(\sum_{x\in G}\phi(x)\cdot x\right)\left(\sum_{y\in G} \psi(y)\cdot y\right)=\sum_{x,y\in G} \phi(x)\psi(y) \cdot(xy)=\sum_{z\in G}\left(\sum_{x\in G} \phi(x)\psi(x^{-1}z)\right)\cdot z\]이 성립하므로 이러한 곱셈을 선택하는 것이 자연스럽다. 가령 $\delta_x$와 $\delta_y$의 곱은 $0$이지만, 이 둘의 convolution은 $\delta_{xy}$이므로, group action에 포함되는 다음의 식
\[(\delta_x\ast \delta_y)\cdot v=\delta_x\cdot(\delta_y\ast v)\]와 같은 것들이 말이 되기 위해서는 이러한 선택이 필연적이다.
임의의 $G$-representation $\rho:G\rightarrow \Aut(V)$에 대하여, 다음의 식
\[\widetilde{\rho}\left(\sum_{x\in G} \phi_x x, v\right)= \sum_{x\in G} \phi_x\rho(x)v\]은 $V$ 위에 $\mathbb{C}[G]$-module 구조를 준다. 거꾸로 임의의 $\mathbb{C}[G]$-module $V$가 주어졌다 하면, 각 $x\in G$에 대하여 $x$가 $V$에 작용하는 방식을 통해 $G$-representation을 얻을 수 있다.
명제 4 위의 대응들은 categorical equivalence
\[\Rep_\mathbb{C}(G)\cong \lMod{\mathbb{C}[G]}\]을 준다.
즉 우리가 $G$-module이라 부르던 것은, 엄밀히 말하자면 $\mathbb{C}[G]$-module 구조에서 $G\hookrightarrow \mathbb{C}[G]$가 주어졌을 때의 action만 본 것이라 생각할 수도 있다.
실제로 위에서 논의한 대부분의 것들이 이 categorical equivalence로 설명될 수 있다. 가령 임의의 $G$-representation $V$에 대하여, $V$의 subrepresentation은 $V$의 $G$-submodule (정확히는 $\mathbb{C}[G]$-submodule)이다. 또, 정의 3의 tensor product도 납득할만한데, 일반적으로 coproduct $\Delta:A\rightarrow A\otimes A$가 주어진 $\mathbb{K}$-algebra $A$와 두 $A$-module $M,N$에 대하여 이들의 텐서곱을 정의하기 위해서는 $\Delta$를 활용하여
\[A\otimes (M\otimes N)\rightarrow (A\otimes A)\otimes (M\otimes N)\rightarrow (A\otimes M)\otimes (A\otimes N)\rightarrow M\otimes N\]을 사용해야 하고, 이 때 사용하는 coproduct $A\rightarrow A\otimes A$이 $\mathbb{C}[G]$의 경우에는
\[\mathbb{C}[G]\rightarrow \mathbb{C}[G]\otimes \mathbb{C}[G]\]이기 때문이다. 그럼 마찬가지로 정의 3에서 정의한 $\Hom$이 이 $\otimes$와 adjunction 관계에 있고, 이러한 이유로 다소 인위적으로 보이는 정의 3의 $G$-action들이 등장하는 것이다.
특별히 $G$의 subrepresentation과 $\mathbb{C}[G]$-submodule이 같은 것이라는 것을 생각하면, $V$가 irreducible representation인 것은 $V$가 simple $\mathbb{C}[G]$-module인 것과 같다.
마슈케의 정리
이제 우리는 유한군의 표현에 필요한 기본적인 개념들은 대충 살펴보았다. 본격적인 이야기를 시작하기 전에, 임의의 representation $V$에 대하여 다음의 부분공간
\[V^G=\{v\in V\mid g\cdot v=v\text{ for all $g\in G$}\}\]을 생각하자. 이 공간은 $G$-action에 의해 고정되는 벡터들의 공간이며, $G$-invariant space이기도 하지만 그보다 우리가 관찰하고 싶은 것은 자명한 projection map
\[p: V\rightarrow V^G;\qquad v\mapsto \frac{1}{\lvert G\rvert}\sum_{g\in G}g\cdot v\]이 존재한다는 것이다. 특히 이 projection map에 담긴 아이디어, 즉 $G$의 작용들을 모두 더한 후 평균내어 $G$-invariant한 대상을 얻어내는 아이디어는 중요하게 사용된다.
정의 5 $G$-representation $V$ 위의 Hermitian inner product $\langle-,-\rangle$이 $G$-invariant라는 것은 임의의 $g\in G$와 $u,v\in V$에 대하여
\[\langle g\cdot u,g\cdot v\rangle=\langle u,v\rangle\]이 성립하는 것이다. $G$-invariant inner product를 갖는 representation을 unitary representation이라 부른다.
만일 이러한 $G$-invariant inner product가 주어졌다면, 임의의 $g\in G$에 대하여 $\rho(g)\in \Aut(V)$는 unitary operator이다. 이를 관찰하기 위해 $G$-invariant inner product $\langle -,-\rangle$가 주어졌다 하고, 임의의 $g\in G$에 대해
\[\langle v,w\rangle=\langle \rho(g) v,\rho(g) w\rangle=\langle \rho(g)^\dagger \rho(g)v,w\rangle\]이
한편, 유한차원 $G$-module $V$는 $G$-invariant inner product를 갖는다. 이는 위에서 언급한 아이디어를 활용하여 증명할 수 있다.
명제 6 임의의 representation $V$는 $G$-invariant inner product를 갖는다. 즉 임의의 representation은 unitary representation이다.
증명
$V$ 위의 임의의 Hermitian inner product $\langle -,- \rangle$에 대하여,
\[\langle\kern-1.5pt\langle u,v\rangle\kern-1.5pt\rangle = \frac{1}{|G|}\sum_{g \in G} \langle g\cdot u, g\cdot v \rangle\]을 통해 새로운 inner product $\langle\kern-1.5pt\langle-,-\rangle\kern-1.5pt\rangle$를 정의하면 된다. 그럼 임의의 $h\in G$에 대하여
\[\langle\kern-1.5pt\langle h\cdot u, h\cdot v\rangle\kern-1.5pt\rangle = \frac{1}{|G|}\sum_{g \in G} \langle gh\cdot u, gh\cdot v \rangle = \langle\kern-1.5pt\langle u, v\rangle\kern-1.5pt\rangle\]이므로 이 inner product는 $G$-invariant이다.
어쨌든 이번 섹션의 핵심적인 정리는 위의 명제로부터 따라나온다.
따름정리 7 (Maschke) 임의의 유한차원 $G$-representation $V$와 $G$-invariant subspace $W$에 대하여, 적당한 $G$-invariant subspace $W’$가 존재하여 $V = W \oplus W’$이도록 할 수 있다. 따라서, 귀납적으로, 임의의 유한차원 $G$-representation은 irreducible representation들의 direct sum으로 분해된다.
증명
$W’$를 $W$의 orthogonal complement로 잡으면, $W’$ 또한 $G$-invariant subspace이며 $V = W \oplus W’$가 성립한다.
앞서 우리는 categorical equivalence
\[\Rep_\mathbb{C}(G)\cong \lMod{\mathbb{C}[G]}\]을 살펴보았다. 그럼 따름정리 7이 주장하는 것은 임의의 유한차원 $G$-representation $V$는 항상 semisimple $\mathbb{C}[G]$-module이라는 것이다. 따라서 $\mathbb{C}[G]$는 그 자체로 Artinian semisimple ring이 되며 (semisimple) 따라서 Artin-Wedderburn 정리 (artin-wedderburn)에 의하여 simple module들로의 decomposition
\[\mathbb{C}[G]\cong \bigoplus_{i=1}^r \Mat_{n_i}(\mathbb{C})\tag{1}\]이 존재한다는 것을 안다.
슈어 직교성
다음 글에서 우리는 decomposition (1)에 표현론적인 의미를 부여한다. 이를 위한 준비작업으로 우리는 다음 보조정리를 증명한다.
보조정리 8 (Schur) (Compact) group $G$와 irreducible $G$-module들 $V,W$가 주어졌다 하자. 그럼 다음이 성립한다.
- 임의의 $G$-map $V\rightarrow W$는 zero map이거나 isomorphism이다.
- 임의의 $G$-automorphism $f\in \Aut_G(V)$는 $f(v)=\lambda v$의 꼴이다.
- $G$-map들의 모임 $\Hom_G(V,W)$은 $\mathbb{C}$이거나 $0$이다.
증명
- 이는 kernel과 image를 각각 생각하면 자명하다.
- 주어진 $f$는 $G$-linear map이기 이전에 $\mathbb{C}$-linear map이므로, $f$의 eigenvalue $\lambda$가 존재한다. 이제 이 eigenvalue에 대응되는 eigenspace를 $W$라 하고, 이것이 실은 $G$-submodule이 됨을 보이면 된다.
- 위의 두 명제에 의해 자명하다.
이를 사용하면 우리는 다음 명제를 얻는다.
명제 9 위와 같은 상황에서, 다음의 함수
\[d=\bigoplus_{W\in\Irr(G, \mathbb{C})} d_W:\bigoplus_{W\in \Irr(G, \mathbb{C})}\Hom_G(W,V)\otimes_\mathbb{C}W\rightarrow V\]는 isomorphism이다.
이에 대한 증명은, $V$가 irreducible decomposition $V=\bigoplus V_j$을 가지므로 다음의 식
\[\Hom_G(W, V)=\Hom_G\left(W, \bigoplus V_j\right)\cong \bigoplus \Hom_G(W, V_j)\]과 보조정리 8에 의해 자명하다. 즉 복잡하게 써 두기는 했지만, 위의 $d$는 각각의 irreducible $G$-module $W$(의 isomorphism class)들이 $V$ 안에 얼마나 들어있는지를 세는 것이며, 따라서 다음 정의가 자연스럽다.
정의 10 위의 함수에 의한 $W\in\Irr(G, \mathbb{C})$의 image를 $V$의 $W$-isotypical summand라 부르고, $\Hom_G(W, V)$를 $W$의 multiplicity라 부른다.
약간의 믿음을 가지면 이러한 표현이 유일하다는 것도 납득할 수 있다. 즉, 우리는 임의의 representation $V$가 주어졌을 때 이를 다음의 decomposition
\[V=V_1^{\oplus r_1}\oplus\cdots\oplus V_k^{\oplus r_k}\]의 형태로 나타낼 수 있는 것을 안다.

댓글남기기