대칭대수와 외대수

대칭대수와 외대수

Tensor algebra $\mathcal{T}(M)$은 그 자체로도 흥미로운 대수적 대상이지만, 특별히 $\mathcal{T}(M)$에서 만들어지는 두 quotient algebra 구조가 중요하다.

우선 임의의 $x,y\in M$에 대해, commutator $x\otimes y-y\otimes x$으로 생성되는 two-sided ideal $\mathfrak{a}$를 생각하자. 특히 $\mathfrak{a}$는 차수 2짜리 homogeneous element들로 생성되므로, §등급대수, ⁋보조정리 2에 의해 $\mathfrak{a}$는 graded ideal이고 따라서 $\mathcal{T}(M)/\mathfrak{a}$는 graded algebra 구조를 갖는다.

이번에는 임의의 $x\in M$에 대하여, $x\otimes x$들로 생성되는 two-sided ideal $\mathfrak{b}$를 생각하자. 그럼 마찬가지로 $\mathfrak{b}$는 차수 2짜리 homogeneous element들로 생성되므로 graded ideal이다. 따라서 $\mathcal{T}(M)/\mathfrak{b}$ 또한 graded algebra 구조를 갖는다.

정의 1 위의 논의에서, quotient algebra $\mathcal{T}(M)/\mathfrak{a}$를 $M$의 symmetric algebra_대칭대수, 그리고 $\mathcal{T}(M)/\mathfrak{b}$를 $M$의 exterior algebra_외대수라 부른다. $M$의 symmetric algebra는 $\mathcal{S}(M)$, 그리고 $M$의 exterior algebra는 $\bigwedge(M)$으로 표기한다.

대칭대수

편의상 quotient map $\mathcal{T}(M)\rightarrow\mathcal{T}(M)/\mathfrak{a}=\mathcal{S}(M)$을 $p$로 표기하고, $p\circ\iota:M\rightarrow \mathcal{S}(M)$을 $q$로 표기하자.

대칭대수의 universal property

다음은 symmetric algebra $\mathcal{S}(M)$의 가장 기초적인 성질이다.

명제 2 $\mathcal{S}(M)$은 commutative algebra이다.

증명

임의의 $x,y\in M$에 대하여,

\[q(x)q(y)-q(y)q(x)=(p\circ\iota)(x)(p\circ\iota)(y)-(p\circ\iota)(y)(p\circ\iota)(x)=p(\iota(x)\iota(y)-\iota(y)\iota(x))=0\]

가 성립한다. 한편 $\mathcal{S}(M)$은 $q(x)$들로 생성되고, 이러한 원소들이 모두 commute하므로 원하는 명제가 성립한다.

뿐만 아니라, 다음의 universal property로부터 $\mathcal{S}(M)$을 이러한 성질을 갖는 가장 작은 $A$-algebra로 생각할 수도 있다.

정리 3 $A$-module $M$을 고정하고, $A$-algebra $E$로의 $A$-module homomorphism $f:M\rightarrow E$가 모든 $x,y\in M$에 대해 $f(x)f(y)=f(y)f(x)$를 만족한다 하자. 그럼 다음 diagram을 commute하도록 하는 유일한 $A$-algebra homomorphism $\tilde{f}:\mathcal{S}(M)\rightarrow E$가 존재한다.

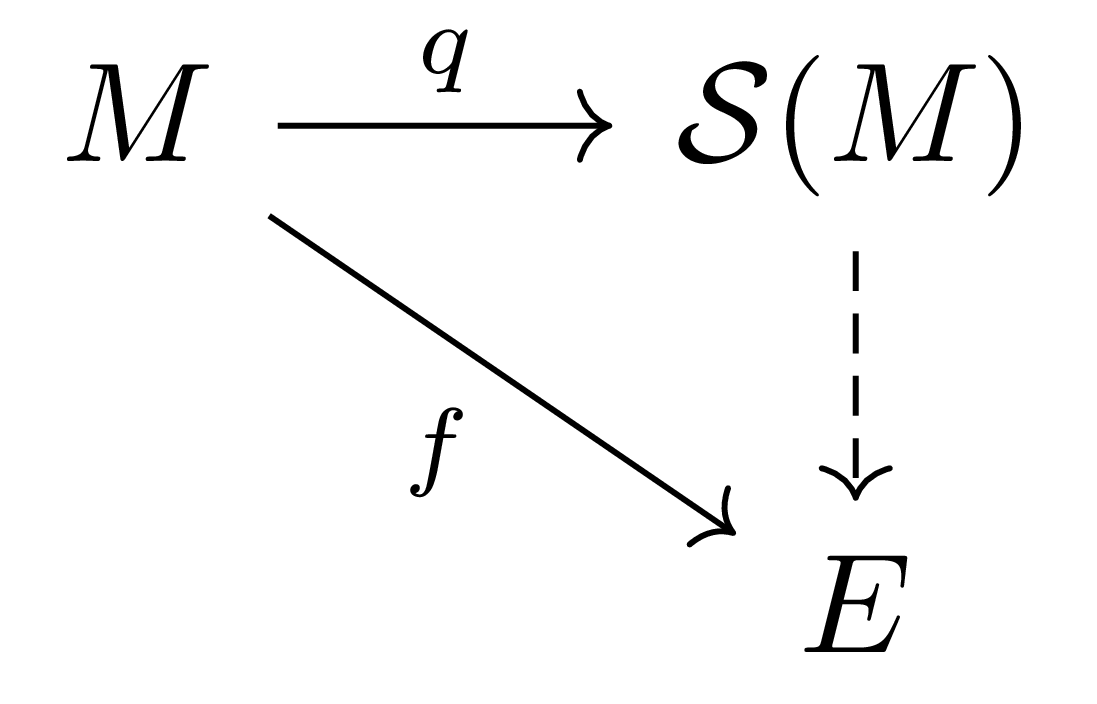
증명

명제 2의 증명과 같이, $\mathcal{S}(M)$들은 $q(x)$들로 생성되므로 $\tilde{f}$는 유일해야 한다는 것이 자명하다. 따라서 존재성만 증명하면 충분하다.

Tensor algebra $\mathcal{T}(M)$의 universal property에 의하여, 다음 diagram을 commute하도록 하는 유일한 $A$-algebra homomorphism $\mathcal{T}(M)\rightarrow E$가 존재한다.

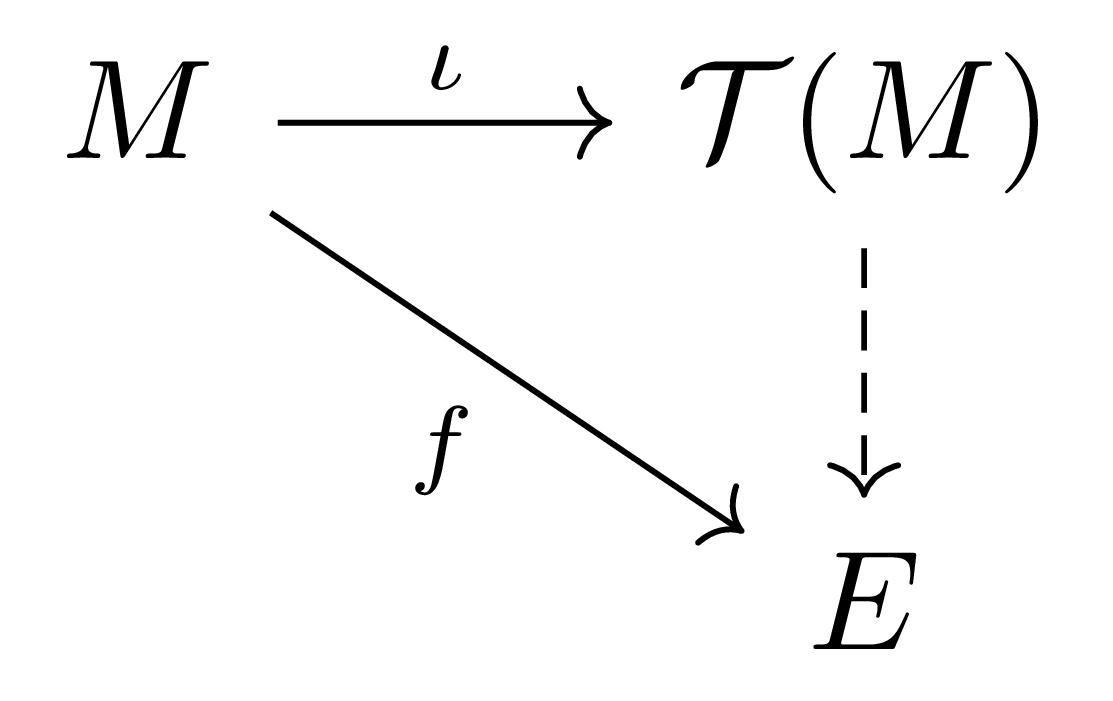
그런데 주어진 조건 $f(x)f(y)-f(y)f(x)=0$에 의해 이 함수의 kernel이 $\mathfrak{a}$를 포함하므로, 다음의 diagram

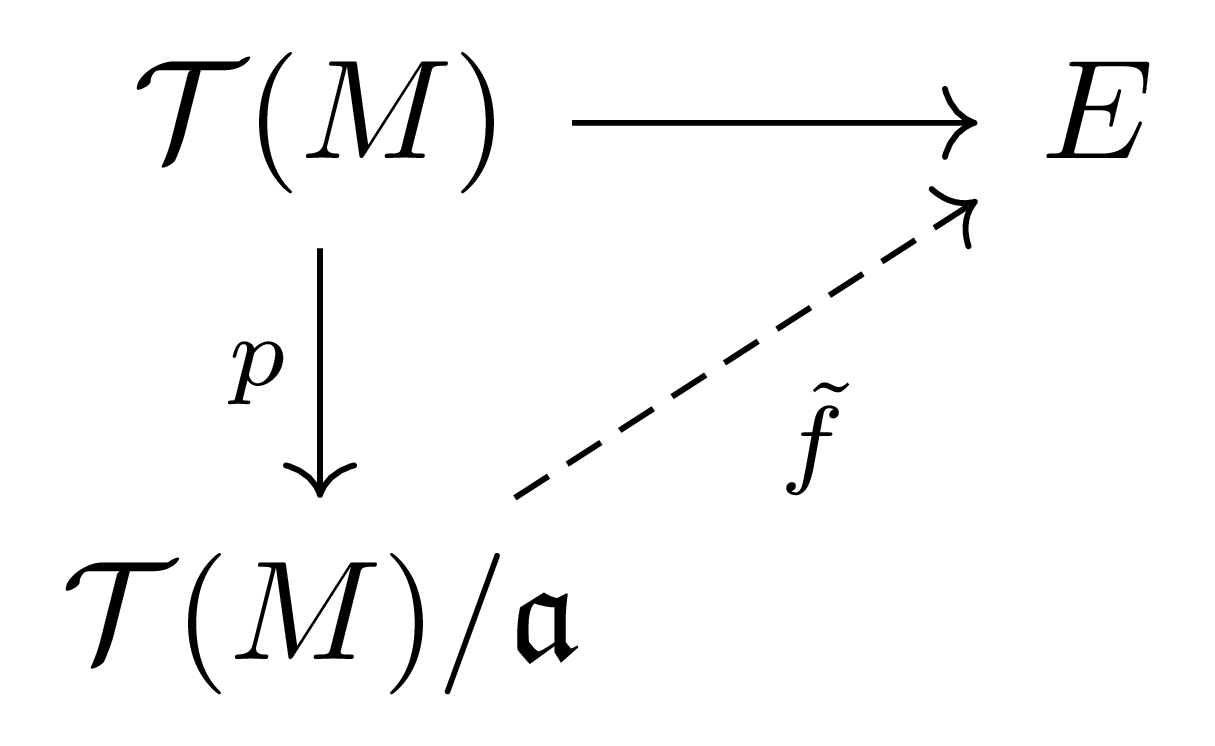
을 commute하도록 하는 유일한 $\mathcal{T}(M)/\mathfrak{a}\rightarrow E$가 존재한다. 이로부터 원하는 결과를 얻는다.

다음 따름정리들은 universal property로부터 쉽게 유도할 수 있다.

따름정리 4 임의의 $A$-module homomorphism $u:M \rightarrow N$에 대하여, 다음 diagram

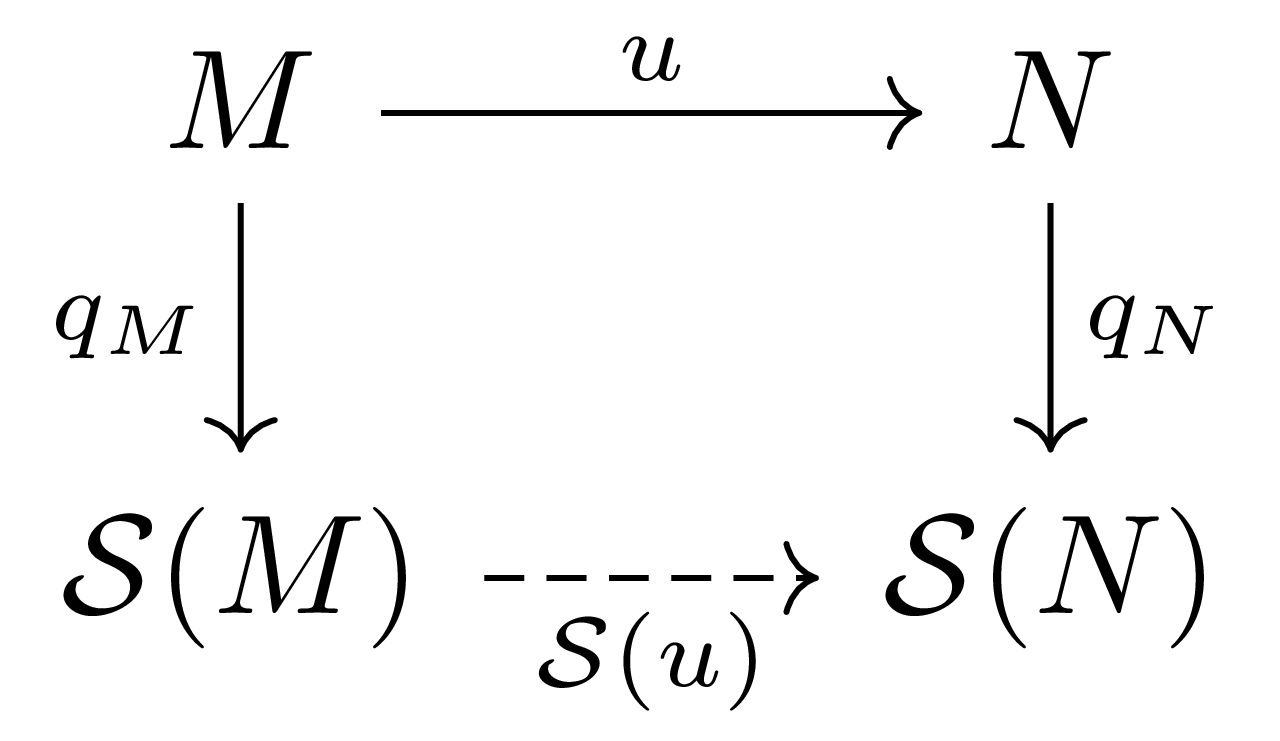
을 commute하도록 하는 유일한 $A$-algebra homomorphism $\mathcal{S}(u)$이 존재한다.

따름정리 5 따름정리 4에서 정의된 $\mathcal{S}(u)$는 합성을 보존한다. 즉 $\mathcal{S}(v\circ u)=\mathcal{S}(v)\circ\mathcal{S}(u)$가 성립한다.

Change of base ring

이제 tensor algebra때와 마찬가지로 스칼라들이 변했을 때 $\mathcal{S}(M)$이 어떻게 변하는지를 살펴본다. 우선 ring homomorphism $\rho:A \rightarrow A’$가 주어졌다 하고, $A$-module $M$, $A’$-module $M’$이 주어졌다 하자. $M’$과 $\mathcal{S}_{A’}(M’)$ 각각을 $A$-module과 $A$-algebra로 생각하면, canonical map $q_{M’}:M’\rightarrow\mathcal{S}_{A’}(M’)$ 또한 $A$-module homomorphism으로 생각할 수 있다.

이제 임의의 $A$-module homomorphism $u:M \rightarrow M’$에 대하여, $q_{M’}\circ u$ 또한 $A$-module homomorphism이고, $q_{M’}$의 성질로부터 정리 3의 조건

\[(q_{M'}\circ u)(x)(q_{M'}\circ u)(y)=(q_{M'}\circ u)(y)(q_{M'}\circ u)(x)\qquad\text{for all $x,y\in M'$}\]

이 만족되는 것을 알 수 있다. 이제 symmetric algebra의 universal property로부터 $A$-module들의 diagram

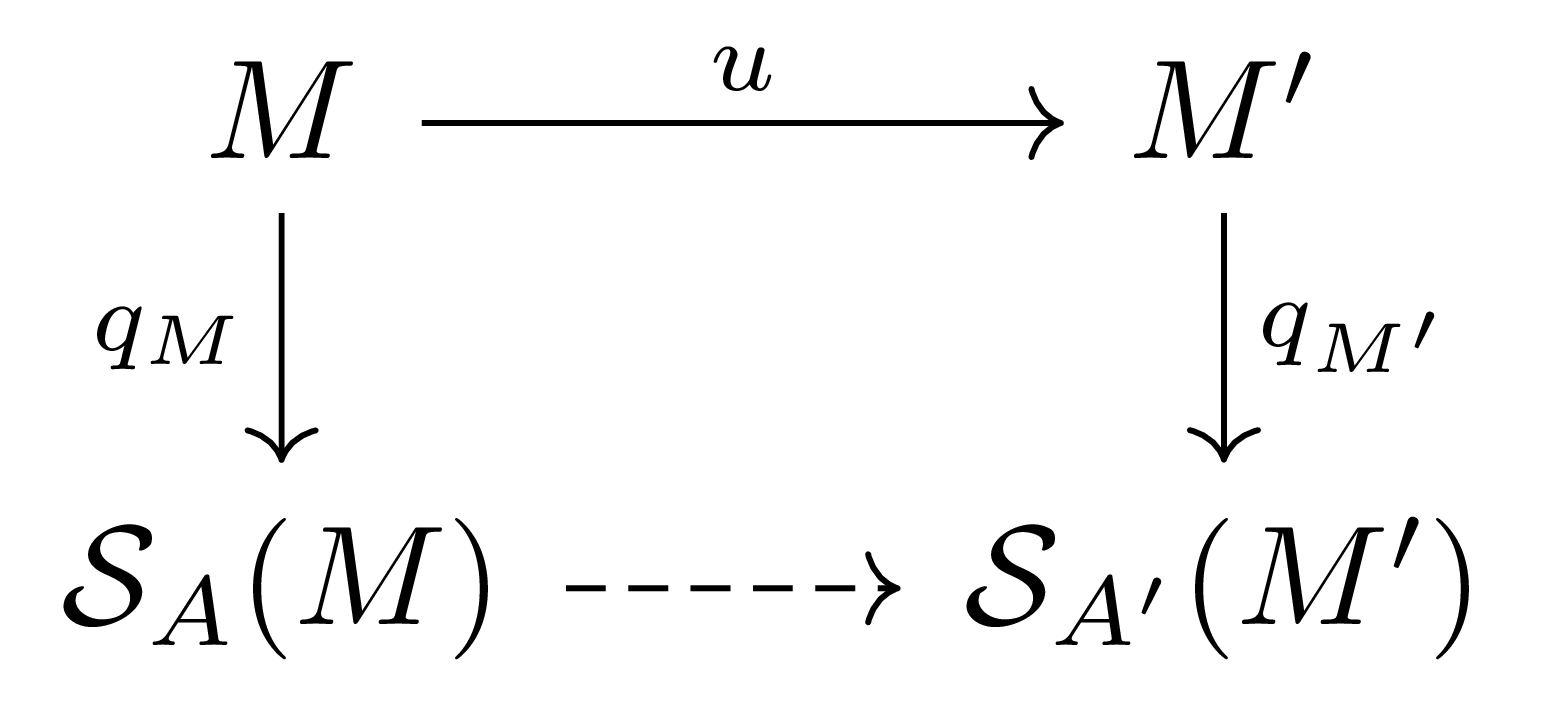
이 commute하도록 하는 유일한 $\mathcal{S}_A(M)\rightarrow\mathcal{S}_{A’}(M’)$이 존재한다. 약간의 abuse of notation을 통해 이 또한 $\mathcal{S}(u)$로 표기한다.

거꾸로 임의의 $A$-module $M$에 대하여, $A’\otimes_AM$은 자연스러운 $A’$-module 구조를 갖는다. 이 module의 symmetric algebra $\mathcal{S}_{A’}(A’\otimes_AM)$을 생각하면, 다음의 $A’$-module homomorphism

\[{\id_{A'}}\otimes q_M:A'\otimes_AM\rightarrow A'\otimes_A\mathcal{S}_A(M)\]

은 임의의 $a’\otimes x,b’\otimes y\in A’\otimes_AM$에 대하여

\[\begin{aligned}({\id_{A'}}\otimes q_M)(a'\otimes x)({\id_{A'}}\otimes q_M)(b'\otimes y)&=(a'\otimes q_M(x))(b'\otimes q_M(y))\\ &=(a'b')\otimes (q_M(x)q_M(y))\\ &=(b'a')\otimes (q_M(y)q_M(x))\\ &=(a'\otimes q_M(x))(b'\otimes q_M(y))\\ &=({\id_{A'}}\otimes q_M)(b'\otimes y)({\id_{A'}}\otimes q_M)(a'\otimes x)\end{aligned}\]

을 만족하고, 따라서 $A’\otimes_AM$의 모든 원소에 대하여 정리 3의 조건이 만족된다. 이로부터 유일한 $A’$-module homomorphism $\mathcal{S}_{A’}(A’\otimes_AM)\rightarrow A’\otimes_A\mathcal{S}_A(M)$을 얻는다.

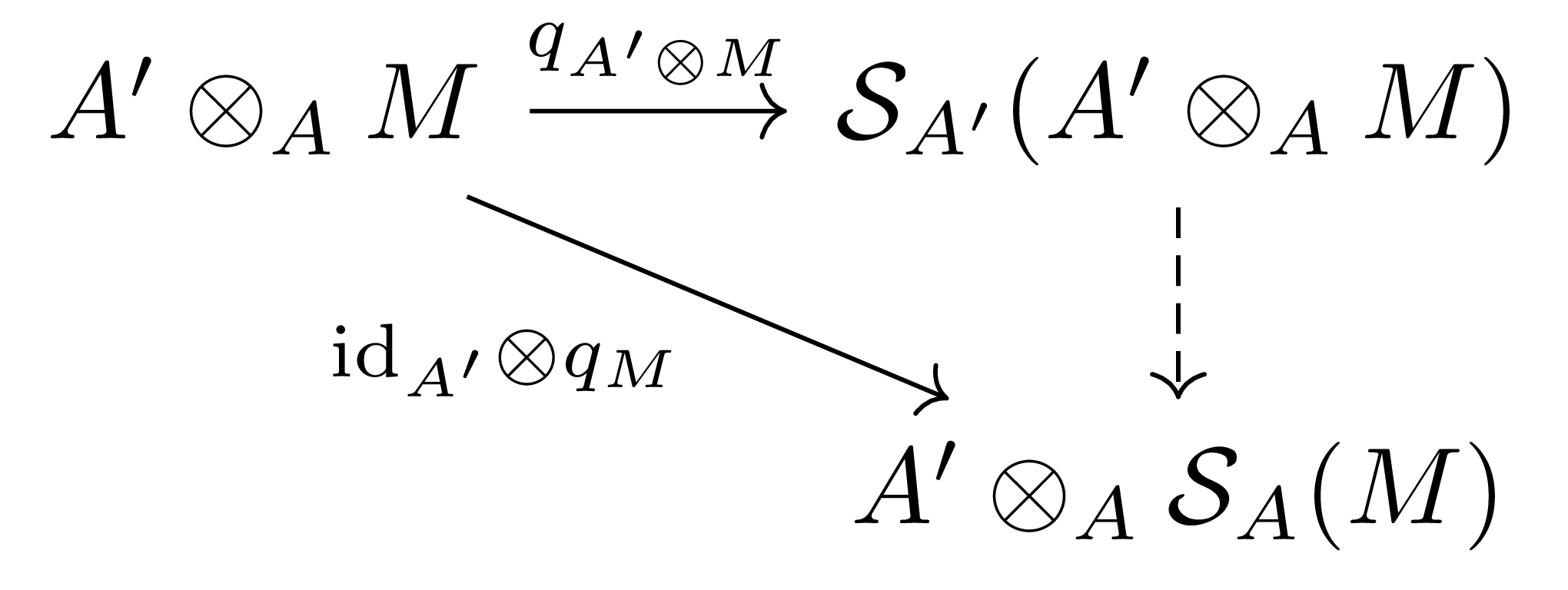
다음 명제는 §다중선형대수, ⁋명제 6과 마찬가지로 증명할 수 있으며, universal property를 보이기 위해서는 위와 같은 방식으로 $q$를 사용하면 된다.

명제 6 위에서 정의한 $\mathcal{S}_{A’}(A’\otimes_AM)\rightarrow A’\otimes_A\mathcal{S}_A(M)$는 isomorphism이다.

직합의 대칭대수

§다중선형대수에서도 $\mathcal{T}(M)$에 대하여 다음 명제와 비슷한 명제를 만들 수 있었을 것이나, 우변이 더 복잡하고 식 자체로는 별 의미가 없어 다루지 않았던 것이다.

명제 7 $A$-module들의 유한한 family $(M_i)_{1\leq i\leq n}$가 주어졌다 하자. 그럼 $M=\bigoplus M_i$에 대하여,

\[\mathcal{S}(M)\cong\bigotimes_{i=1}^n\mathcal{S}(M_i)\]

이 성립한다.

증명

Direct sum으로의 canonical injection $\iota_i:M_i\rightarrow M$에 대하여, $\mathcal{S}(\iota_i):\mathcal{S}(M_i)\rightarrow\mathcal{S}(M)$들이 잘 정의된다. 또, $\mathcal{S}(M)$이 commutative algebra이므로

\[\mathcal{S}(M_1)\times\cdots\times\mathcal{S}(M_n)\rightarrow\mathcal{S}(M)\]

를 $\mathcal{S}(\iota_1)\times\cdots\times\mathcal{S}(\iota_n)$으로 정의해도 문제가 생기지 않는다. 따라서 tensor product의 universal property에 의하여

\[\bigotimes_{i=1}^n\mathcal{S}(M_i)\rightarrow \mathcal{S}(M)\]

이 잘 정의된다.

이제 이 함수의 역함수를 만들어야 한다. 우선 각각의 $i$에 대하여, canonical map들의 합성

\[M_i\rightarrow\mathcal{S}(M_i)\rightarrow\bigotimes_{i=1}^n \mathcal{S}(M_i)\]

을 생각할 수 있다. 이제 direct sum의 universal property로부터

\[\bigoplus_{i=1}^n M_i=M\rightarrow\bigotimes_{i=1}^n\mathcal{S}(M_i)\]

를 얻는다. 이제 $\bigotimes\mathcal{S}(M_i)$는 commutative algebra이므로 정리 2의 조건이 자명하게 성립하고, 따라서 이로부터

\[\mathcal{S}(M)\rightarrow\bigotimes_{i=1}^n\mathcal{S}(M_i)\]

를 얻는다.

외대수

위에서 증명한 명제들을 외대수에 대해서도 반복할 수 있다. 증명은 모두 대칭대수와 비슷하므로 생략하기로 한다. Exterior algebra로의 canonical map은 symmetric algebra와 마찬가지로 canonical map들의 합성

\[M\rightarrow \mathcal{T}(M)\rightarrow\mathcal{T}(M)/\mathfrak{b}=\bigwedge(M)\]

으로 주어지며, 불필요한 문자낭비를 막기 위해 이 함수에 대한 별도의 문자를 지정하지는 않기로 한다.

외대수의 universal property

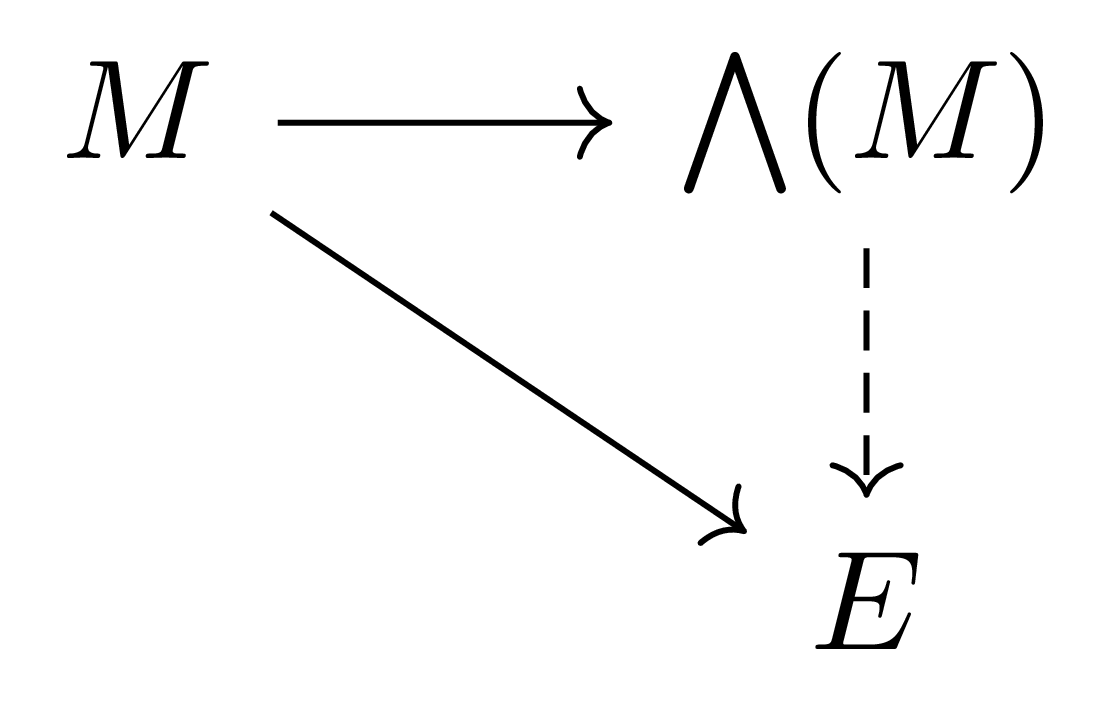
정리 8 $A$-module $M$을 고정하고, $A$-algebra $E$로의 $A$-module homomorphism $f:M\rightarrow E$가 모든 $x\in M$에 대해 $f(x)^2=0$를 만족한다 하자. 그럼 다음 diagram을 commute하도록 하는 유일한 $A$-algebra homomorphism $\tilde{f}:\bigwedge(M)\rightarrow E$가 존재한다.

따름정리 9 임의의 $A$-module homomorphism $u:M \rightarrow M’$에 대하여, 다음 diagram

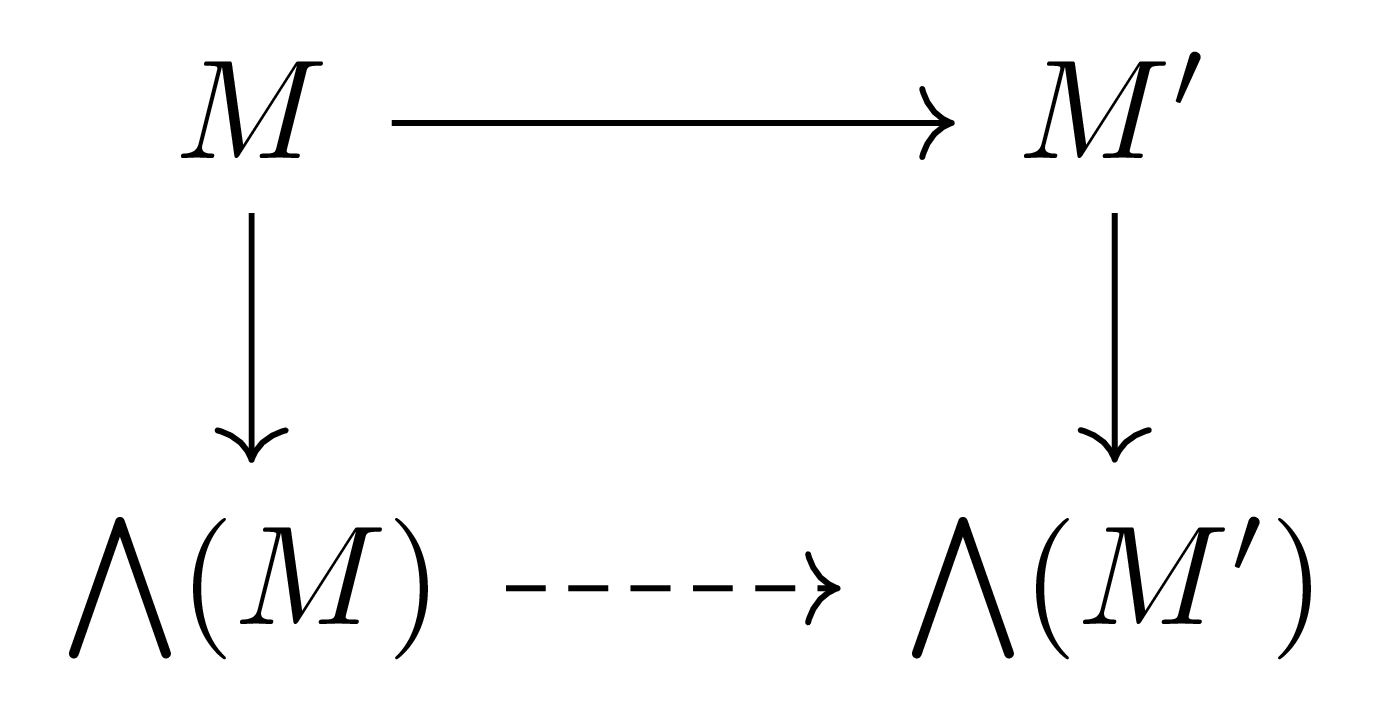
을 commute하도록 하는 유일한 $A$-algebra homomorphism $\bigwedge(u)$이 존재한다.

따름정리 10 따름정리 9에서 정의된 $\bigwedge(u)$는 합성을 보존한다. 즉 $\bigwedge(v\circ u)=\bigwedge(v)\circ\bigwedge(u)$가 성립한다.

Change of base ring

위에서 다룬 대칭대수의 §§§Change of base ring과 같은 상황을 가정하자. 그럼 다음 $A$-module들의 diagram

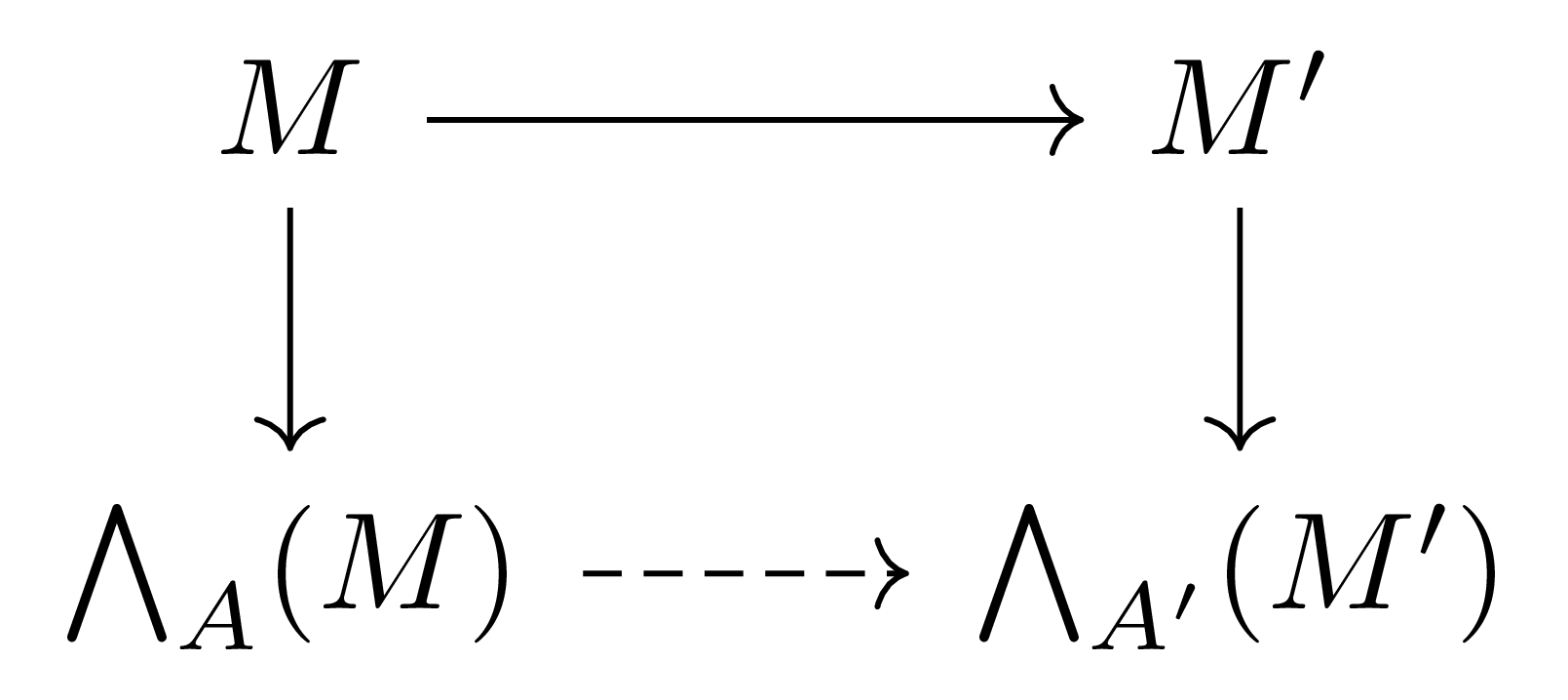
을 commute하도록 하는 $\bigwedge(u):\bigwedge\nolimits_A(M)\rightarrow\bigwedge\nolimits_{A’}(M’)$이 존재한다. 또, 명제 6과 비슷하게 다음이 성립한다.

명제 11 두 ring $A,A’$, 그리고 $A$-module $M$에 대하여

\[\bigwedge\nolimits_{A'}(A'\otimes_AM)\cong A'\otimes_A\bigwedge\nolimits_A(M)\]

이 성립한다.

직합의 외대수

마지막으로 다음 명제 또한 성립한다.

명제 12 $A$-module들의 유한한 family $(M_i)_{1\leq i\leq n}$가 주어졌다 하자. 그럼 $M=\bigoplus M_i$에 대하여,

\[\bigwedge(M)\cong\bigotimes_{i=1}^n\bigwedge(M_i)\]

이 성립한다.

Symmetric power와 alternating power

$\mathcal{S}(M)$과 $\bigwedge(M)$은 모두 graded algebra이므로, 이들을 degree에 따라

\[\mathcal{S}(M)=\bigoplus_{n=0}^\infty\mathcal{S}^n(M),\qquad\bigwedge(M)=\bigoplus_{n=0}^\infty\bigwedge\nolimits^n(M)\]

으로 분해할 수 있다. 이 때 $\mathcal{S}(M)$과 $\bigwedge\nolimits^n(M)$을 각각 $M$의 $n$번째 symmetric power, exterior power라 부른다. $\mathcal{S}(M)$과 $\bigwedge(M)$와 마찬가지로 이들 또한 적당한 universal property를 갖는다. 이를 정리로 쓰기 위해서는 몇 가지 정의가 필요하다.

임의의 $A$-module $X,Y$와 multilinear map $f:X^n\rightarrow Y$에 대하여, $f$가 symmetric이라는 것은 임의의 $\sigma\in S_n$에 대하여

\[f(x_1,\ldots, x_n)=f(x_{\sigma(1)},\ldots, x_{\sigma(n)})\]

이 성립하는 것이다. 비슷하게, $f$가 alternating이라는 것은 임의의 $i,j$에 대하여

\[f(x_1,\ldots, x_i,\ldots, x_j,\ldots, x_n)=-f(x_1,\ldots, x_j,\ldots, x_i,\ldots, x_n)\]

이 성립하는 것이다. 이러한 상황에서 $\mathcal{S}(M)$과 $\bigwedge\nolimits^n(M)$의 universal property는 다음과 같이 서술된다.

정리 13 임의의 $A$-module $M,N$이 주어졌다 하고, 자연수 $n$을 고정하자. 그럼

• $M^n$에서 $N$으로의 symmetric multilinear map과, $\mathcal{S}^n(M)$에서 $N$으로의 linear map 사이의 일대일대응이 존재한다.
• $M^n$에서 $N$으로의 alternating multilinear map과, $\bigwedge\nolimits^n(M)$에서 $N$으로의 linear map 사이의 일대일대응이 존재한다.

---

참고문헌

[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.

---