텐서대수

이제 드디어 텐서 대수를 정의한다. 이번 글에서 $A$는 항상 commutative ring with unity인 것으로 가정한다. 또, 편의상 $\mathbb{N}$-graduation이 주어진 구조를 모두 간단하게 graded라 부르기로 한다.

텐서대수의 정의

임의의 $A$-module $M$에 대하여,

\[\mathcal{T}^n(M)=M^{\otimes n}=\underbrace{M\otimes\cdots\otimes M}_\text{\small $n$ times}\]

으로 정의하자. $n=0$인 경우 $\mathcal{T}^0(M)=A$인 것으로 생각한다. 그럼 $\mathcal{T}(M)$을 다음의 식

\[\mathcal{T}(M)=\bigoplus_{n\geq 0}\mathcal{T}^n(M)\]

으로 정의할 수 있다. $A$를 trivial $\mathbb{N}$-graduation

\[A=A\oplus 0\oplus\cdots\]

이 주어진 것으로 생각하면, $\mathcal{T}(M)$이 graded $A$-module 구조를 갖는다.

한편 $\mathcal{T}(M)$에서의 곱셈을 정의하기 위해서는 $\mathcal{T}(M)$의 homogeneous element들

\[x\in M,\quad x\otimes y\in M\otimes M,\quad\cdots\]

에 대해서만 정의하면 충분하다. 임의의 자연수 $p,q$에 대하여, $\mathcal{T}^p(M)$과 $\mathcal{T}^q(M)$의 homogeneous element들의 곱을 다음의 식

\[(x_1\otimes\cdots\otimes x_p)\cdot (x_{p+1}\oplus\cdots\oplus x_{p+q})=x_1\otimes\cdots x_p\otimes x_{p+1}\otimes\cdots\otimes x_{p+q}\in\mathcal{T}^{p+q}(M)\]

으로 정의하자. 그럼 텐서곱의 associativity로부터 $\mathcal{T}(M)$이 associative algebra인 것을 확인할 수 있으며, 뿐만 아니라 $1\in A=\mathcal{T}^0(M)$이 이 곱셈의 항등원 역할을 하므로 $\mathcal{T}(M)$은 항등원을 갖는다.

정의 1 위와 같이 정의한 associative unital $\Delta$-graded $A$-algebra $\mathcal{T}(M)$을 $M$의 tensor algebra_텐서대수라 부른다. 이 때, canonical injection $M=\mathcal{T}^1(M)\hookrightarrow\mathcal{T}(M)$을 canonical injection이라 부른다.

텐서대수의 universal property

Tensor algebra 또한 다음과 같은 universal property를 갖는다.

정리 2 임의의 unital $A$-algebra $E$와, $A$-linear map $f:M\rightarrow E$가 주어졌다 하자. 그럼 유일한 $A$-algebra homomorphism $\tilde{f}:\mathcal{T}(M)\rightarrow E$가 존재하여 $f=\tilde{f}\circ\iota$를 만족한다.

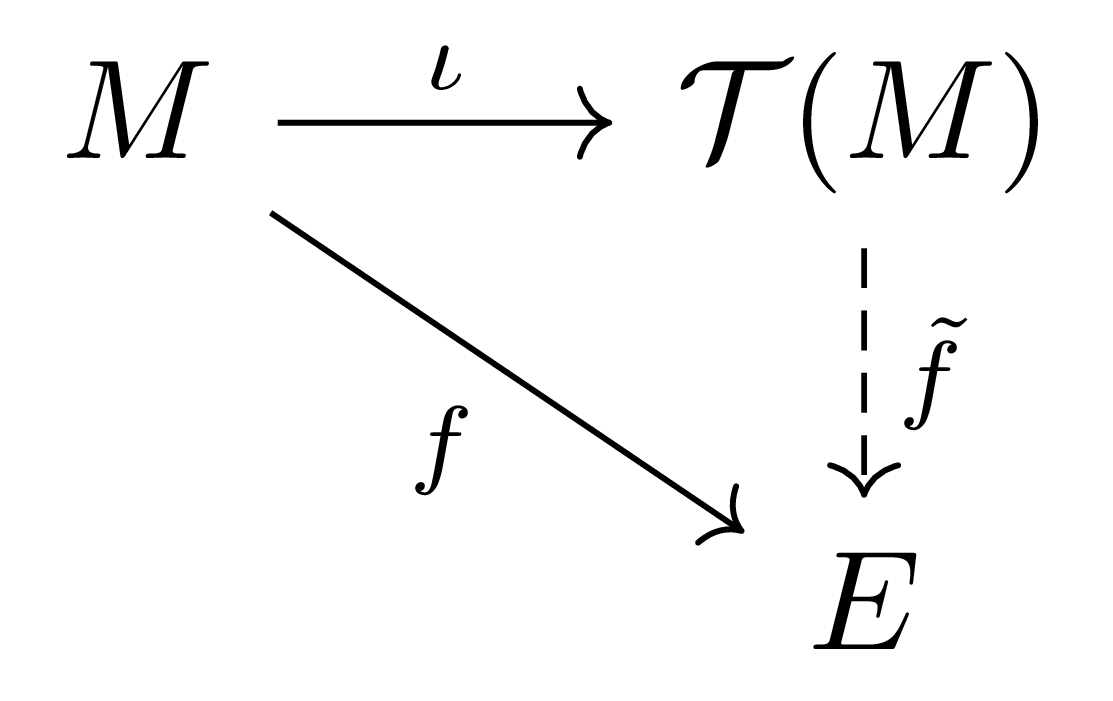
증명

우선 이러한 성질을 만족하는 $\tilde{f}$, $\bar{f}$가 존재한다 가정하자. 임의의 $x_1\otimes\cdots\otimes x_n\in\mathcal{T}(M)$에 대하여,

\[\tilde{f}(x_1\otimes\cdots\otimes x_n)=\bar{f}(\iota(x_1)\otimes\cdots\otimes\iota(x_n))=\bar{f}(\iota(x_1))\cdots\bar{f}(\iota(x_n))=f(x_1)\cdots f(x_n)\]

이고, 비슷한 식이 $\bar{f}$에 대해서도 성립하므로 $\tilde{f}(x_1\otimes\cdots\otimes x_n)=\bar{f}(x_1\otimes\cdots\otimes x_n)$이 성립한다.

이제 다음의 식

\[\tilde{f}(x_1\otimes\cdots\otimes x_n)=f(x_1)\cdots f(x_n)\]

을 통해 각각의 원소 $x_1\otimes\cdots\otimes x_n$에 대해 $\tilde{f}$를 정의하고, 이를 확장하여 $\mathcal{T}^n(M)$ 위에서 $\tilde{f}$를 잘 정의할 수 있다. 그럼 direct sum의 universal property에 의하여, 이를 $\mathcal{T}(M)$ 전체로 확장할 수 있으며, 이렇게 얻어진 $\tilde{f}$가 $A$-algebra homomorphism이라는 것을 쉽게 보일 수 있다.

그럼 다음 따름정리들은 위의 정리로부터 명확하다.

따름정리 3 정리 2의 universal property를 만족하는 $\iota:M\rightarrow\mathcal{T}(M)$은 isomorphism에 대하여 유일하다.

증명

또 다른 $\iota’:M\rightarrow \mathcal{T}’(M)$이 존재하여 위의 universal property를 만족한다고 가정하자. 그럼 $\iota:M\rightarrow\mathcal{T}(M)$의 universal property로부터 다음의 diagram을 commute하도록 하는 유일한 $\psi:\mathcal{T}(M)\rightarrow\mathcal{T}’(M)$이 존재한다.

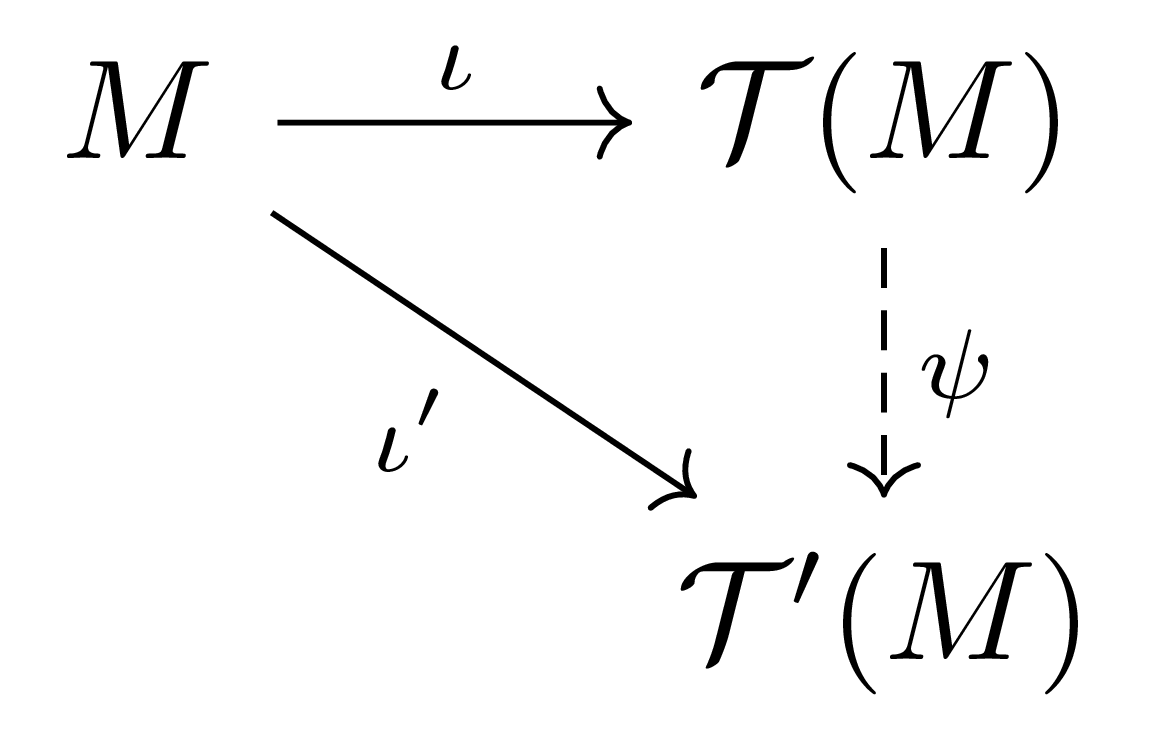
비슷하게 $\iota’:M\rightarrow\mathcal{T}’(M)$의 universal property로부터 다음의 diagram을 commute하도록 하는 유일한 $\phi:\mathcal{T}’(M)\rightarrow\mathcal{T}(M)$이 존재한다.

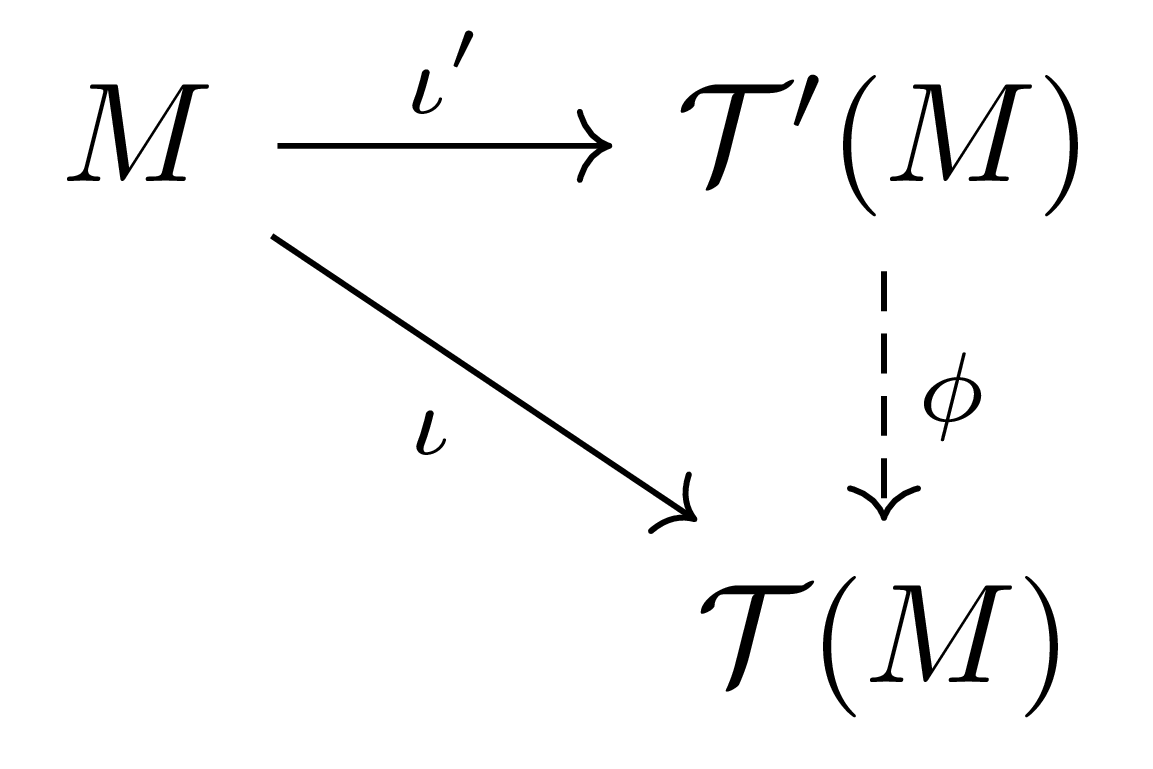
이제 다음의 diagram

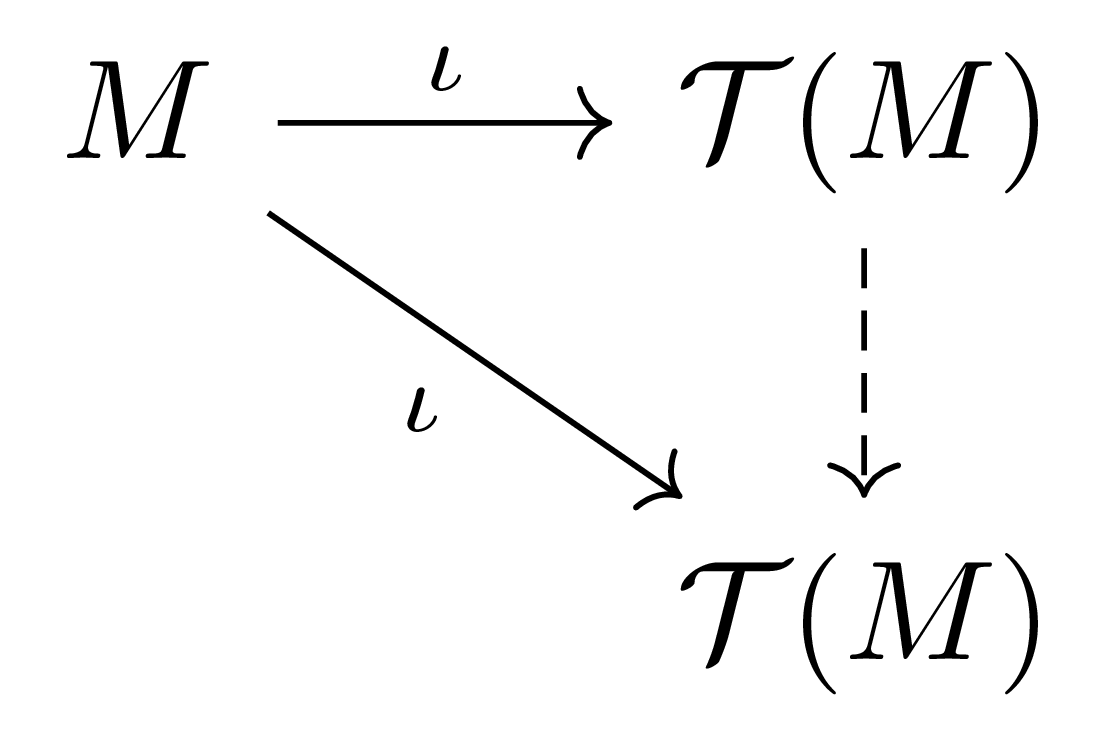
을 commute하도록 하는 $\mathcal{T}(M)\rightarrow\mathcal{T}(M)$ 또한 유일해야 하는데, $\id_{\mathcal{T}(M)}$과 $\phi\circ\psi$가 모두 이를 commute하도록 하므로 $\id_{\mathcal{T}(M)}=\phi\circ\psi$가 성립한다. 비슷하게 $\id_{\mathcal{T}’(M)}=\psi\circ\phi$가 성립한다.

따름정리 4 두 $A$-module 사이의 linear map $u:M\rightarrow N$이 주어졌다 하자. 그럼 유일한 $\mathcal{T}(u):\mathcal{T}(M)\rightarrow\mathcal{T}(N)$이 존재하여 $\iota_N\circ u=\mathcal{T}(u)\circ\iota_M$이 성립한다.

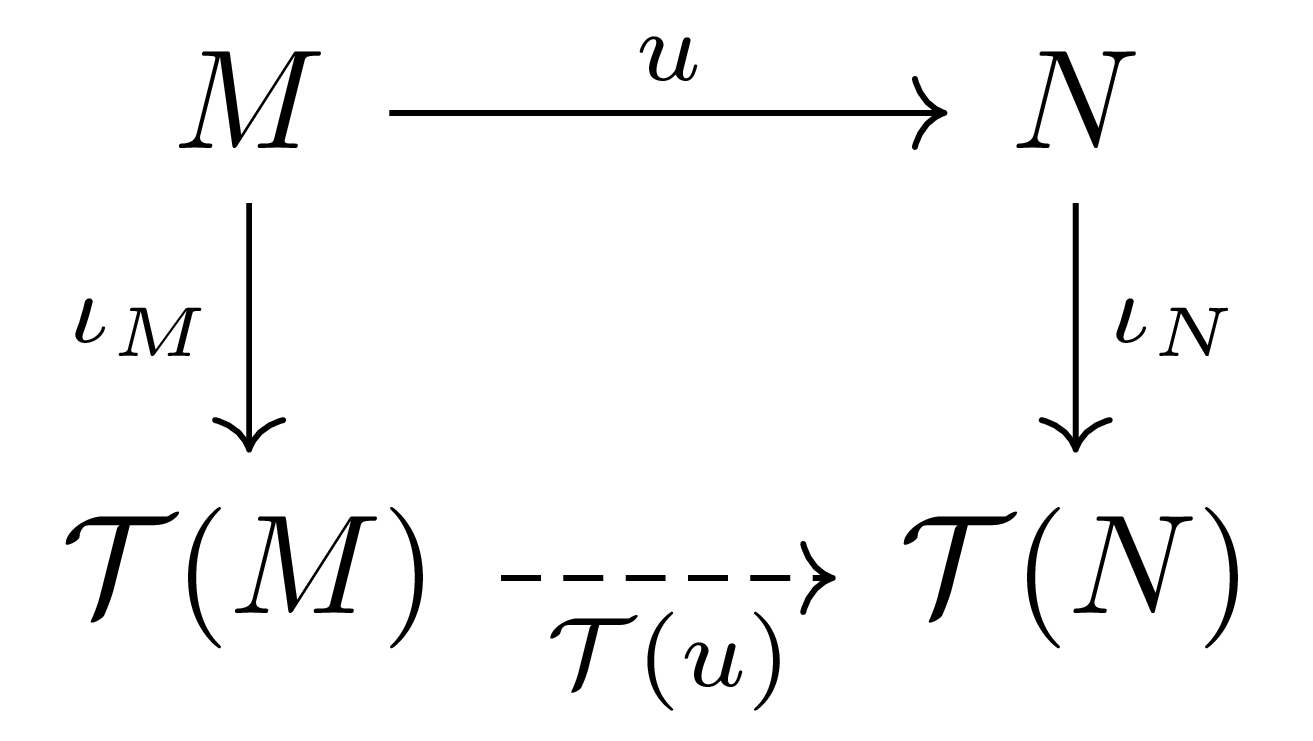
증명

자명

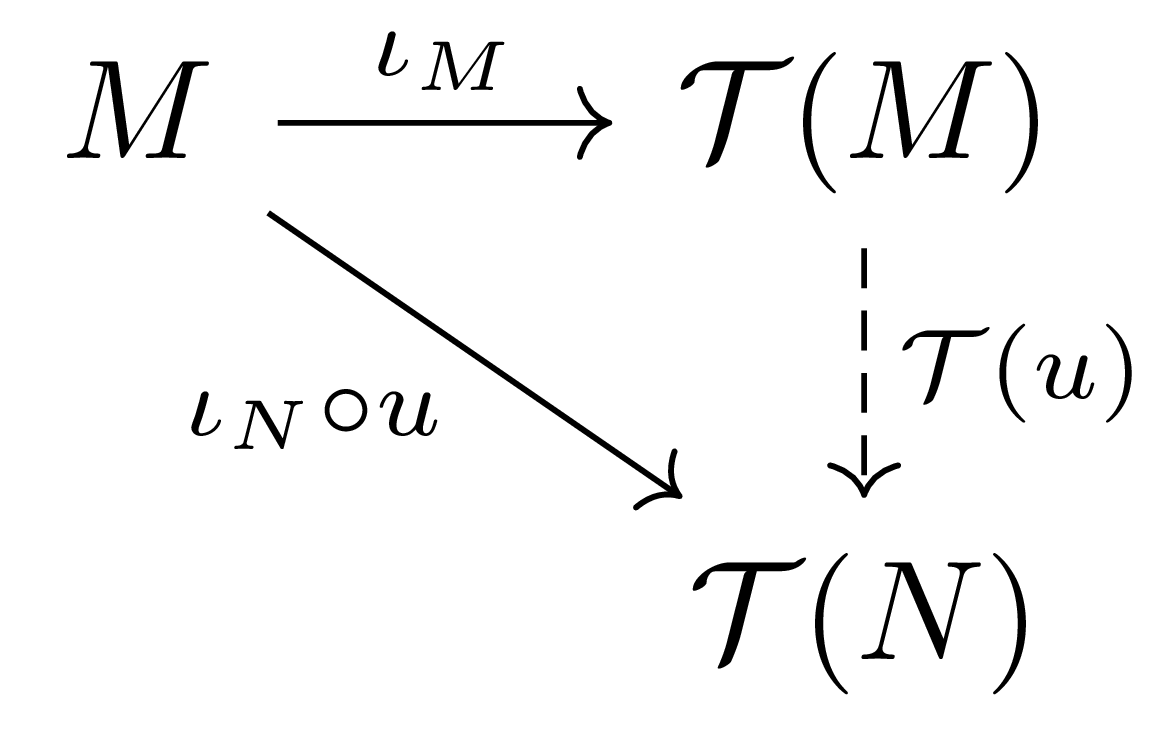
위의 따름정리는 universal property로부터 자명한 방법으로 얻어지지만, $\mathcal{T}(u)$를 각각의 $\mathcal{T}^n(M)$으로 제한한 것을 $\mathcal{T}^n(u)$라 하였을 때

\[\mathcal{T}^n(u)(x_1\otimes\cdots\otimes x_n)=u(x_1)\otimes\cdots\otimes u(x_n)\]

이 성립한다는 것을 관찰하는 것 또한 유용하다.

한편, 다음 따름정리 또한 universal property로부터 자명하다.

따름정리 5 따름정리 4에서 정의된 $\mathcal{T}(u)$는 합성을 보존한다. 즉 $\mathcal{T}(v\circ u)=\mathcal{T}(v)\circ\mathcal{T}(u)$가 성립한다.

증명

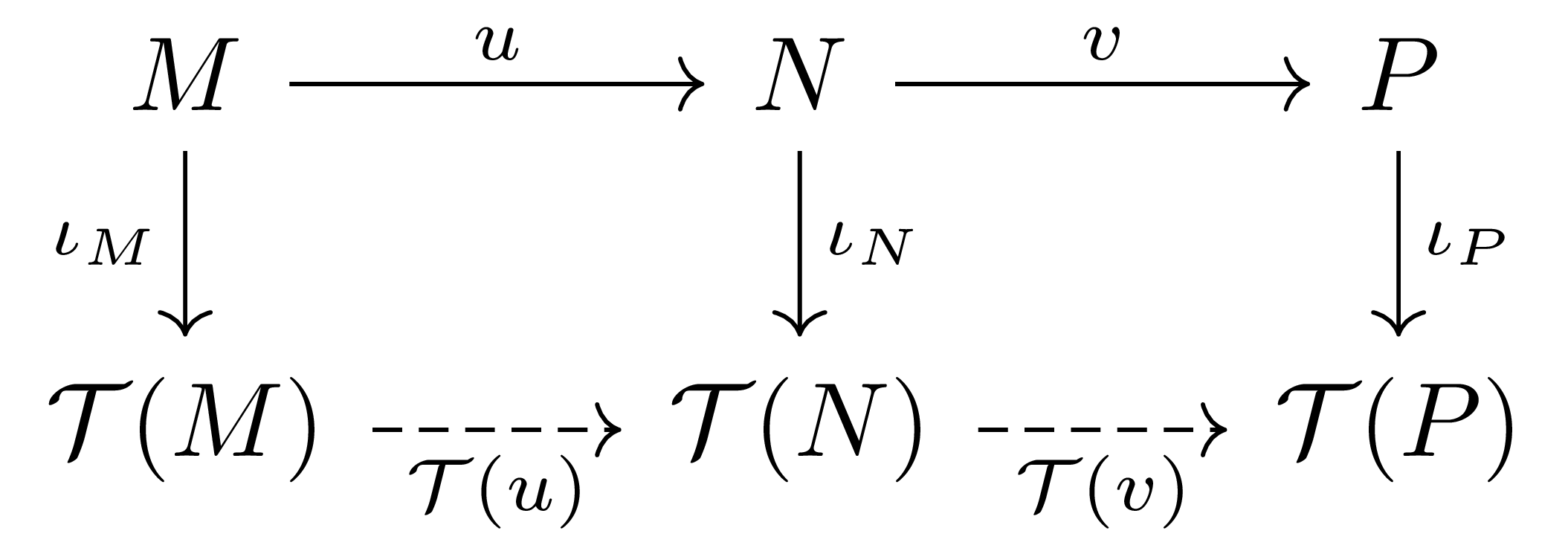
이 따름정리로부터 $M$과 $N$이 isomorphic하다면 $\mathcal{T}(M)$과 $\mathcal{T}(N)$이 isomorphic하다는 것 또한 자명하다.

Change of base ring

Ring homomorphism $\rho:A\rightarrow A’$가 주어졌다 하자. 임의의 $A’$-module $M’$에 대하여, 다음의 식

\[a\cdot m':=\rho(a)\cdot m',\qquad a\in A,m'\in M'\]

을 통해 $M’$을 $A$-module로 생각할 수 있다. 마찬가지 방식으로, $M’$의 tensor algebra $\mathcal{T}_{A’}(M’)$ 또한 $A$-algebra로 생각할 수 있고, 그럼 canonical injection $\iota_{M’}:M’\rightarrow\mathcal{T}_{A’}(M’)$ 또한 $A$-module homomorphism이라 생각할 수 있다.

이러한 상황에서 $A$-module homomorphism $u:M\rightarrow M’$이 주어졌다 하자. 그럼 $\iota_{M’}\circ u$ 또한 $A$-module homomorphism이고 따라서 tensor algebra의 universal property로부터 다음 $A$-module들의 diagram

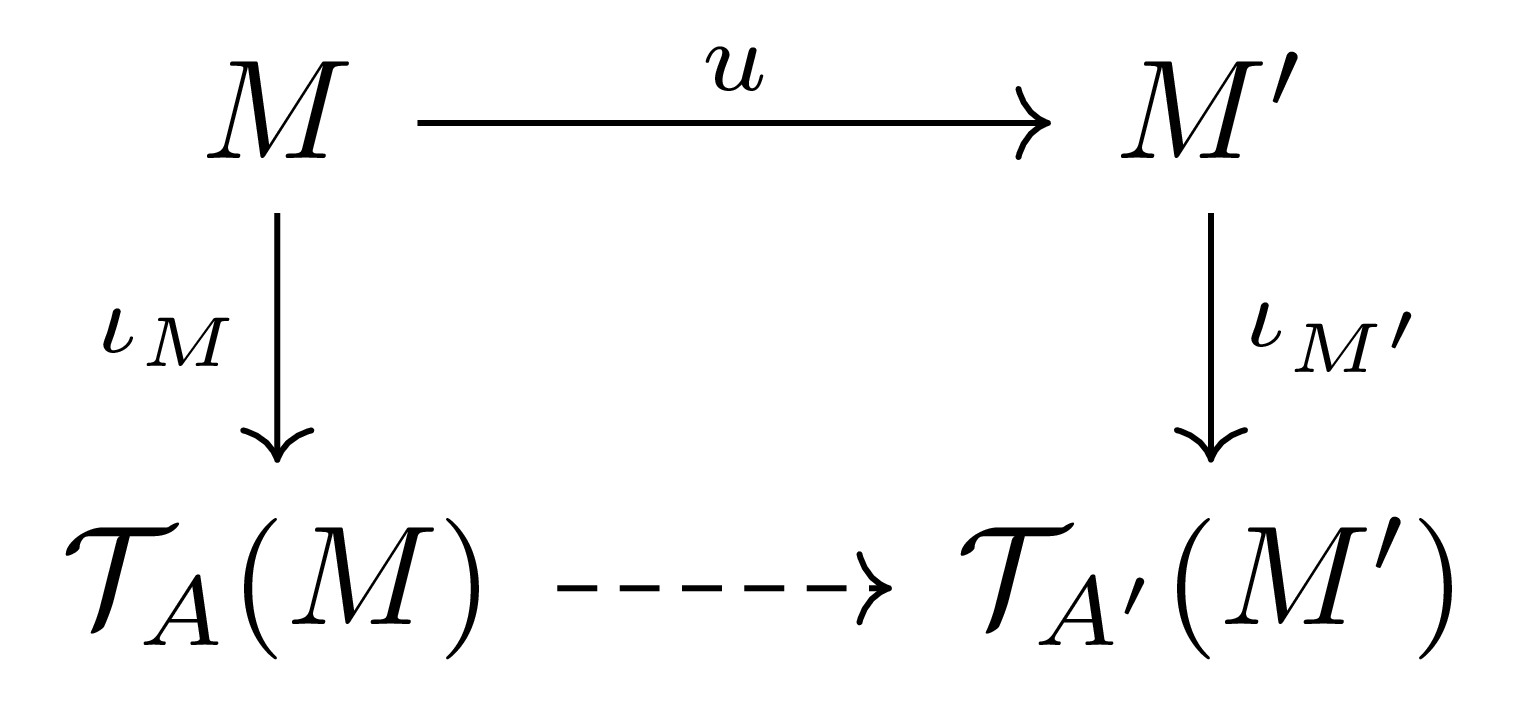
을 commute하도록 하는 유일한 $A$-module homomorphism이 존재한다. 약간의 표기법의 남용을 통해 이 또한 $\mathcal{T}(u)$로 적는다.

거꾸로 임의의 $A$-module $M$에 대하여, $A’\otimes_A M$은 자연스러운 $A’$-module 구조를 갖는다. 이제 $A’$-module $A’\otimes_A M$의 tensor algebra $\mathcal{T}_{A’}(A’\otimes_A M)$를 생각하면 다음의 commutative diagram

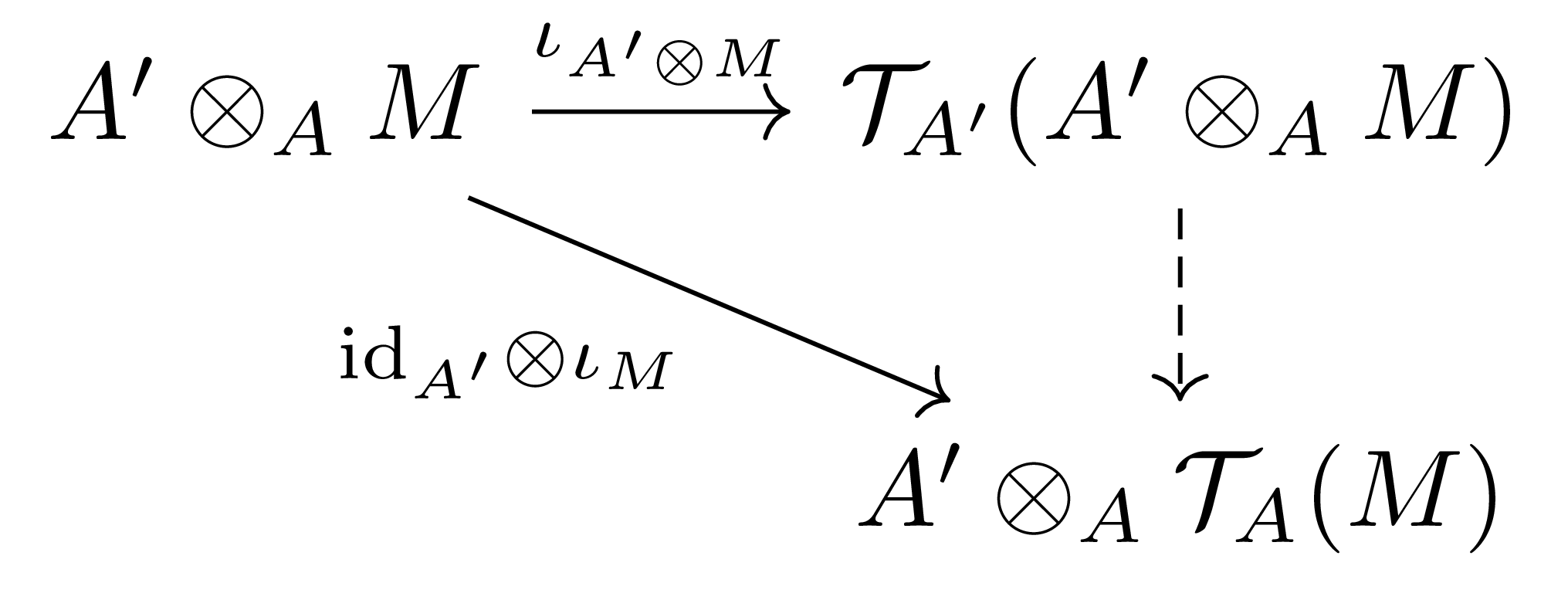
을 얻는다.

명제 6 위에서 얻어지는 $\mathcal{T}_{A’}(A’\otimes_AM)\rightarrow A’\otimes_A\mathcal{T}_A(M)$은 isomorphism이다.

증명

역함수를 만들면 충분하다. 우선 $\mathcal{T}_{A’}(A’\otimes_AM)$을 $A$-algebra로 보면, $\mathcal{T}_A(M)$의 universal property로부터 다음 diagram

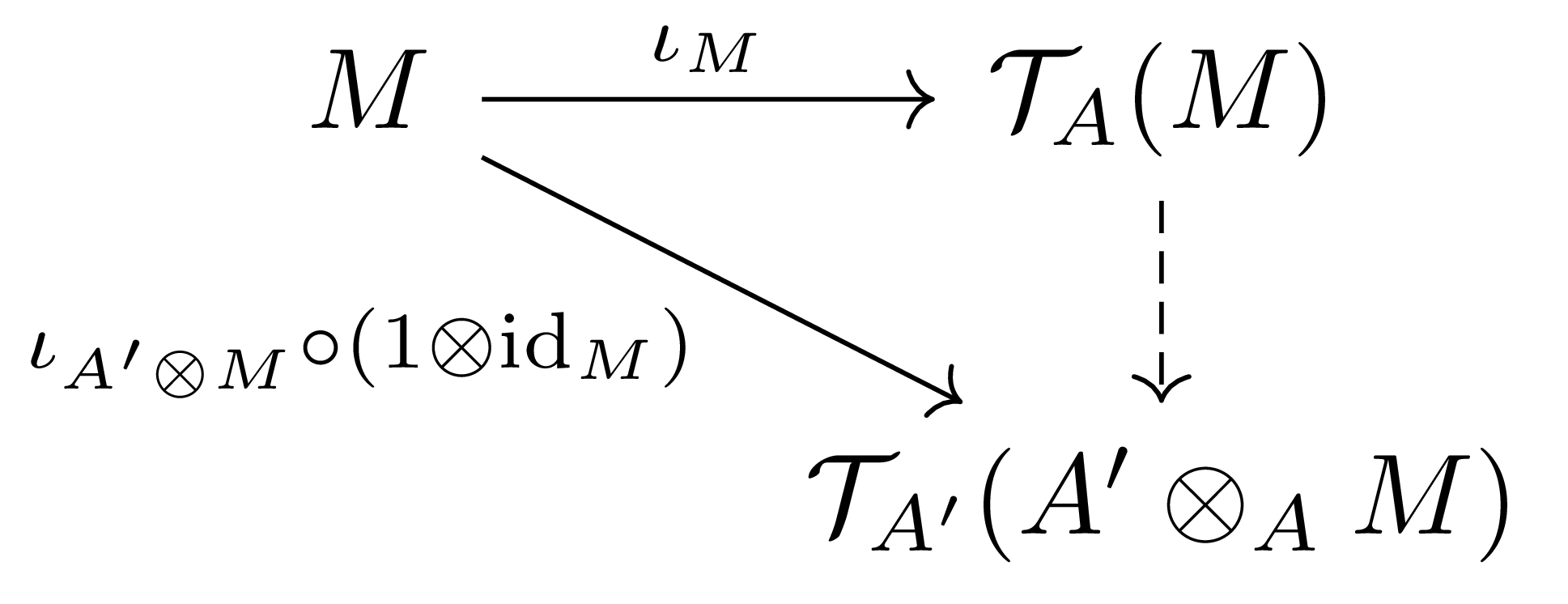
을 commute하도록 하는 $A$-algebra homomorphism $\mathcal{T}_A(M)\rightarrow\mathcal{T}_{A’}(A’\otimes_AM)$이 유일하게 존재한다. 이제 이렇게 얻어진 $A$-algebra homomorphism에 대하여, $A’\otimes_A\mathcal{T}_A(M)$의 universal property로부터 다음의 diagram

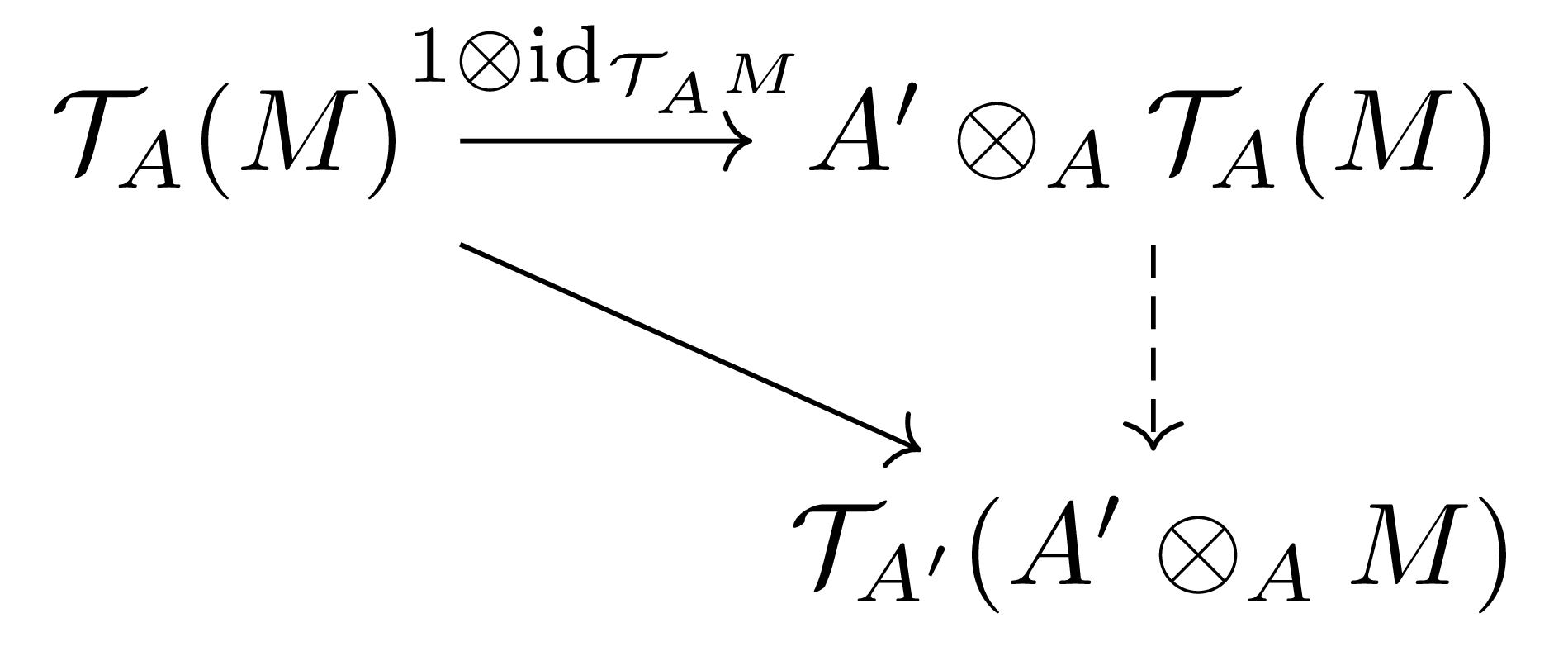
을 commute하도록 하는 유일한 $A’$-algebra homomorphism $A’\otimes_A\mathcal{T}_A(M)\rightarrow\mathcal{T}_{A’}(A’\otimes_AM)$이 존재한다. 이 함수가 위에서 얻은 $\mathcal{T}_{A’}(A’\otimes AM)\rightarrow A’\otimes_A\mathcal{T}_A(M)$의 역함수임을 쉽게 확인할 수 있다.

Mixed tensor

이제 commutative monoid $\Delta$를 $\mathbb{N}\times\mathbb{N}$인 것으로 생각하자. 고정된 $A$-module $M$에 대하여,

\[\mathcal{T}^{r,s}(M)=\underbrace{M\otimes\cdots\otimes M}_\text{$r$ copies}\otimes\underbrace{M^\ast\otimes\cdots\otimes M^\ast}_\text{$s$ copies}\]

으로 정의한다. 특별히 $r=s=0$인 경우는 $\mathcal{T}^{0,0}(M)=A$인 것으로 생각한다. 이제 앞선 정의들에서와 마찬가지로 direct sum

\[\mathcal{T}^{\bullet,\bullet}(M)=\bigoplus_{(r,s)\in\Delta} \mathcal{T}^{r,s}(M)\]

를 생각하면 $\mathcal{T}^{\bullet,\bullet}(M)$이 $\Delta$-graded $A$-algebra가 되는 것은 자명하다. 여기에서 $\mathcal{T}^{\bullet,\bullet}(M)$의 두 원소 (simple tensor들)

\[x=x_1\otimes x_2\otimes\cdots\otimes x_{r_1}\otimes \alpha^1\otimes \alpha^2\otimes\cdots\otimes \alpha^{s_1}, \quad y=y_1\otimes y_2\otimes\cdots\otimes y_{r_2}\otimes \beta^1\otimes \beta^2\otimes\cdots\otimes \beta^{s_2}\]

에 대하여 곱셈 $x\otimes y$는

\[x\otimes y=x_1\otimes \cdots\otimes x_{r_1}\otimes y_1\otimes \cdots\otimes y_{r_2}\otimes \alpha^1\otimes\cdots\otimes \alpha^{s_1}\otimes \beta^1\otimes\cdots\otimes \beta^{s_2}\in \mathcal{T}^{r_1+r_2, s_1+s_2}(V)\tag{1}\]

으로 정의된다. 그럼 우리는 $\mathcal{T}^{\bullet,\bullet}(M)$를 $M$ 위에서의 mixed tensor algebra라 부르고, 이들의 원소를 mixed tensor라 부른다.

정의에 의해 $\mathcal{T}^{r,0}(M)=\mathcal{T}^r(M)$이고 $\mathcal{T}^{0,s}(M)=\mathcal{T}^s(M^\ast)$이다. 만일 $M$이 finitely generated projective $A$-module이라면

\[\theta_M:M^\ast_AM\rightarrow\End_A(M)\]

을 다음의 식

\[\theta_M(x^\ast\otimes x)(y)=x^\ast(y)x\]

으로 정의할 수 있으며, 이는 isomorphism이 된다.

---

참고문헌

[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.

---