근계

리 군의 표현론

임의의 유한군 $G$가 주어졌을 때 이를 잘 살펴보는 방법 중 하나는 그 유한차원 representation

\[\rho:G\rightarrow \Aut(V)\]

을 보는 것이다. $V$의 basis를 선택하고 나면 $\rho$에 의한 $G$의 image를 다루는 것은 선형대수에 불과하므로 우리는 $G$의 구조를 훨씬 쉽게 알아낼 수 있다.

Lie group의 경우 이러한 표현론적 관점은 더 도움이 되는데, Lie group은 $\GL(n;\mathbb{R})$이나 $\Diff(M)$과 같이, 본질적으로 다른 대상 위에 작용하는 것이기 때문이다.

다만 [표현론] §유한군의 표현론, ⁋정의 1에서처럼 $G$의 representation theory를 정의하면 Lie group $G$ 위에 있는 smooth structure는 놓치게 되므로, 다음과 같이 정의해주어야 한다.

정의 1 Lie group $G$에 대하여, $G$의 representation_표현은 유한차원 벡터공간 $V$와, smooth map

\[\rho:G\rightarrow \Aut(V)\]

이 주어진 것이다.

만일 $G$를 discrete topology와 자명한 smooth structure가 주어진 Lie group으로 본다면 이 정의는 [표현론] §유한군의 표현론, ⁋정의 1의 일반화라 생각할 수도 있다. 비슷하게 [표현론] §유한군의 표현론, §§표현론의 기본 개념들에 있는 모든 정의를 Lie group에 대해서도 할 수 있다.

이 글에서 중요한 역할을 했던 것은 group $G$가 유한군이라는 사실이었다. 가령 $G$의 모든 원소에 대해 평균을 내는 아이디어는 이러한 사실을 바탕으로 했다. 이를 Lie group으로 일반화하기 위해서는 $G$에 어떠한 종류의 유한성을 강제해야 한다.

우리는 따라서 $G$가 compact Lie group인 경우를 종종 다루게 된다. 이 경우, locally compact Hausdorff space로서 $G$ 위에는 Haar measure가 존재하며 따라서 $G$의 원소들에 대한 합을 $G$ 전체에 대한 적분으로 바꿔 쓸 수 있다. 이제 이 Haar measure에 대한 $L^2$ space $L^2(G)$를 생각하면 우리는 다음의 식

\[(g\cdot f)(x)=f(g^{-1}x)\]

을 통해 $G$의 $L^2(G)$ 위에서의 action을 정의할 수 있으며, 이는 Haar measure의 translation invariance에 의해 unitary representation이 된다. 한편 우리가 character를 정의할 때, $\rho(g)$의 trace를 사용했는데, 이는 matrix coefficient

\[L\circ \rho\]

으로 일반화한다. 여기서 $\rho:G\rightarrow \Aut(V)$는 representation이고 $L:\Aut(V)\rightarrow \mathbb{C}$는 linear functional이다. 그럼 다음이 성립한다.

정리 1 (Peter-Weyl) 다음이 성립한다.

1. $G$의 matrix coefficient들은 $G$ 위에서 정의된 continuous complex function들의 공간 $C(G)$에서 dense하다.
2. Compact group $G$의 Hilbert space $H$로의 unitary representation $\rho:G\rightarrow \Aut(H)$가 주어진다면, $H$는 $G$의 finite-dimensional irreducible unitary representation들의 orthogonal direct sum으로 쓸 수 있다.

3. 특별히 위의 결과를 $H=L^2(G)$에 적용하면, 다음의 decomposition

   \[L^2(G)=\mathop{\widehat{\bigoplus}}_{\pi\in\mathrm{Irr}(G)}E_\pi^{\oplus \dim E_\pi}\]

   이 성립한다.

우리는 이러한 결과를 사용하지는 않을 것이므로 별도의 증명은 없이 넘어가지만, 어쨌든 표현론의 도구들이 Lie group들을 살펴보는 데에 큰 도움이 된다는 것은 확인할 만하다.

넣어야 할것 finite grp rep 에서 Lie grp rep으로 각각의 \rho(g)들에 해당하는 simultaneous eigenvector

몰루

우리는 앞선 글에서 Lie group과 Lie algebra를 탐구하는 도구로서 이들의 representation을 도입했다. 가령 Lie group $G$의 representation $G\times V \rightarrow V$가 주어진다면, 이는 $G\rightarrow\Aut(V)$가 주어진 것과 같으므로 matrix Lie group들과 그 subgroup들을 살펴보아 원래의 Lie group에 대한 정보를 알 수 있을 것이었다.

한편 우리의 기본적인 철학은, 이를 정당화하기에는 약간의 설명이 추가로 필요하지만, $G$-representation $G\times V \rightarrow V$는 결국 선형대수로 취급할 수 있다는 것이고 앞선 글에서 우리는 선형대수에서 기초적인 개념들, 가령 §리 군의 표현, ⁋정의 10과 같은 것들을 이 analogy에 넣는 작업을 하였다.

Adjoint representation

우리는 §리 군, ⁋정의 19에서 Lie group $G$의 adjoint representation $G\rightarrow \Aut(\mathfrak{g})$을 정의했다. 이를 통해 우리는 임의의 Lie group을 (basis의 선택을 거친다면) matrix Lie group으로 생각할 수 있다. 우리가 다루는 많은 경우 $G$는 유한차원이고, 따라서 그 tangent space인 $\mathfrak{g}$ 또한 유한차원일 것이므로 Lie group을 살펴보는 것은, 조금 과장해서 말하자면, 선형대수학을 하는 것과 다를 바가 없다.

한편 누군가가 선형대수학에서 가장 불만족스러운 부분을 (굳이) 꼽으라고 한다면, 그 중 하나는 임의의 두 행렬들이 교환법칙을 만족하지 않는다는 것이다. 이는 필연적인 것이지만, 만일 어떠한 벡터공간 $V$가 두 subspace들의 direct sum $V_1\oplus V_2$로 표현되고, 두 행렬 $A_1$, $A_2$가 각각 $V_1$에서 $V_1$, $V_2$에서 $V_2$로의 linear operator에 대응되는 행렬이라면 이들 행렬이 commute한다는 것을 안다. 이 상황은

원환면의 작용

많은 경우 $\mathfrak{g}$이 complex vector space인 것이 편하므로, 필요한 경우에는 $\mathfrak{g}$의 complexification을 $\mathfrak{g}$로 쓰기도 한다. (정의 3)

이렇게

한편 simply connected, compact Lie group $G$는 항상 torus를 포함한다. 이를 살펴보기 위해 임의의 $g\in G$를 택한 후 이로부터 생성되는 $G$의 subgroup $\langle g\rangle$을 생각하자. 그럼 이 subgroup의 $G$에서의 closure는

이는 가령, 고정된 방향 $X\in \mathfrak{g}$으로의 exponential map이 정의하는 곡선을 생각하고 $G$가 compact라는 사실을 이용하면 확인할 수 있다. 우리는 우선 다음을 정의한다.

정의 1 Compact connected Lie group $G$에 대하여, $G$의 subgroup $T$가 maximal torus라는 것은 $T$가 torus이고, $T\subsetneq T’ \subset G$를 만족하는 torus $T’$가 존재하지 않는 것이다.

한편 우리는 임의의 torus $T$에 대하여, $T$는 abelian이고 따라서 $T$의 임의의 irreducible representation $V$는 $1$차원이라는 것을 안다. 바꾸어 말하자면, 임의의 representation $T\rightarrow\Aut(V)$가 주어졌다 하면, 이를 irreducible subrepresentation으로 분해하여 다음의 식

\[V=\bigoplus_{i}V_i\]

을 얻고, 각각의 $V_i$는 $1$차원이다. 이 때 각각의 $V_i$ 위에서는 $T$의 action이 훨씬 명시적인데, 이는 $V_i$가 $1$차원인 것으로부터 $\Aut(V_i)\cong \mathbb{C}^\times$이므로, torus action은 continuous homomorphism $\chi_{\lambda_i}:T \rightarrow \Aut(V_i)\cong \mathbb{C}^\times$로 주어지기 때문이다. 뿐만 아니라 이것이 irreducible이므로 $\lvert\lambda\rvert=1$이고 따라서 각각의 $V_i$ 위에서 torus action은

\[t\cdot v=\chi_{\lambda_i}(t)v,\qquad \chi_{\lambda_i}(t)\in S^1\subset\mathbb{C}^\times\]

으로 주어진다. 한편 우리는 다음의 식

\[\chi_{\lambda_i}(\exp(X))=e^{2\pi i \lambda_i(X)}\qquad\text{for all $X\in \mathfrak{t}$}\tag{1}\]

을 통해 $T$의 character $\chi_{\lambda_i}$와 $\mathfrak{t}$ 위에 정의된 linear functional $\lambda_i$ 사이의 일대일 대응이 있는 것을 안다.

직관적으로 $t\mapsto e^{2\pi i\lambda_i(X)}$를 각속도 $\lambda_i(X)$를 갖는 각운동이라 생각할 수 있고, 이러한 관점을 도입하면 우리는 각각의 $X\in \mathfrak{t}$가 주어졌을 때, 이 방향으로의 각속도 $\lambda_i(X)$가 얼마인지를 통해 이 torus action을 설명할 수 있다는 것을 안다. 이 때 각각의 $\lambda_i$들을 우리는 weight라 부른다. 그럼 우리는 각각의 weight $\lambda_i$마다 적당한 $V_i$가 존재하여, 이 위에서는 torus action이 $t\cdot v=\chi_{\lambda_i}(t)v$로 작동하는 것을 안다. 이러한 $V_i$를 weight space라 부른다.

예시 2 특별한 예시로, 1차원 torus

\[S^1\cong T \cong \mathbb{R}/\mathbb{Z}\]

을 생각하면, $S^1$은 다음의 집합

\[S^1=\left\{e^{2\pi i t}\mid t\in \mathbb{R}/\mathbb{Z}\right\}\]

으로 생각할 수 있다. 이제 이 집합이 2차원 벡터공간 $\mathbb{C}^2$ 위에 다음의 식

\[e^{2\pi i t}\cdot (z_1,z_2)=(e^{4\pi i t}z_1, e^{-2\pi i t}z_2)\]

으로 act한다고 하자. 이 action은 작위적으로 보이지만, 위에서 살펴본 것과 같이 임의의 torus $T$와 임의의 representation $V$가 주어졌다면 $V$의 irreducible decomposition을 생각하고 각각의 irreducible component의 basis $e_i$들을 택하면 모든 torus action은 (적당한 basis의 선택에 의해) 이러한 꼴로 나타나는 것을 안다.

이를 행렬로 나타내면, 위의 action은 $\GL(2;\mathbb{C})$의 원소(들의 family)

\[\begin{pmatrix}e^{4\pi i t}&0\\0&e^{-2\pi i t}\end{pmatrix}\]

로 나타낼 수 있다. 이 때 이 행렬의 trace $e^{4\pi i t}+e^{-2\pi i t}$가 바로 이 representation의 character이다.

이 action의 weight space는 $\span(e_1), \span(e_2)$임이 자명하며, 가령 $\span(e_1)$에 해당하는 weight는 다음의 식

\[\chi_{\lambda_1}(\exp (X))=e^{2\pi i \lambda_1(X)}\qquad\text{for all $X\in \mathfrak{t}$}\]

을 만족하는 linear functional $\lambda_1:\mathfrak{t}\rightarrow \mathbb{C}$으로 주어진다. 이는 당연히 $1\in \mathbb{R}$을 $2$로 보내는 $\lambda_1(t)=2t$에 의해 정의되며 따라서 이 weight space에 해당하는 weight는 (약간의 abuse of notation을 통해) $2$라 할 수 있다. 이 때 $\lambda$가 위의 식을 만족하기 위해서는, $e^{2\pi i}=1$이므로, 반드시 $\lambda(1)\in \mathbb{\mathbb{Z}}$여야 한다.

더 일반적으로 만일 $r$차원 torus의 action이 주어졌다면 $\mathfrak{t}$는 $\mathbb{R}^r$일 것이며, 이 때 torus $T$를

\[T^r=\left\{(e^{2\pi i t_1}, \ldots e^{2\pi i t_r})\mid t_i\in \mathbb{R}/\mathbb{Z}\right\}\]

으로 쓴다면 그 Lie algebra $\mathfrak{t}\cong \mathbb{R}^r$ 중 weight가 될 수 있는 것은 $\mathbb{Z}^r$에 속하는 원소이며 따라서 weight $\lambda$는 다음의 $r$-tuple

\[\lambda=(n_1, \ldots, n_r)\]

로 주어질 것이다. 명시적으로 이 weight는 임의의 $X=(x_1,\ldots, x_r)\in \mathfrak{t}$가 주어졌을 때 $n_1x_1+\cdots+n_rx_r$을 내놓는 linear functional이다.

직관적으로 weight decomposition은 일종의 eigenspace decomposition으로 생각할 수 있으며, 이것이 우리가 real vector space 대신 complex vector space를 생각하는 이유이다. 한편 eigenspace decomposition에서와 마찬가지로, 각각의 weight에 대한 중복도가 $1$일 필요는 없다. 가령 다음의 torus action

\[e^{2\pi i t}\cdot(z_1, z_2)=(e^{4\pi i t}z_1, e^{4\pi i t} z_2)\]

를 생각하면 이번에는 2차원 공간 $\mathbb{C}^2$ 위에서 $T$가 weight $2$를 갖는 것처럼 행동하기 때문이다. 이와 같이 서로 같은 weight $\lambda$들을 갖는 성분들을 한데 모아 이를 $V_\lambda$라 하면, 우리는 weight space decomposition $V=\bigoplus V_\lambda$를 얻는다. 지금까지의 논의를 엄밀하게 정의로 적으면 다음과 같다.

정의 3 Torus $T$와 complex $T$-module $V$가 주어졌다 하자. Irreducible character $\chi_\lambda: T \rightarrow S^1$와 그에 해당하는 linear functional $\lambda:\mathfrak{t}\rightarrow\mathbb{C}$에 대하여, $\lambda$가 $V$의 weight이라는 것은 다음 집합

\[V_\lambda=\left\{v\in V\mid t\cdot v=\chi_\lambda(t)v\text{ for all $t\in T$}\right\}\]

이 nontrivial인 것이다. 이 때, $V_\lambda$를 $\lambda$의 weight space라 하며, decomposition

\[V=\bigoplus_\lambda V_\lambda\]

을 $V$의 weight decomposition이라 부른다.

특히 이를 위의 상황에 적용하면, 우리는 임의의 simply connected compact Lie group $G$와 $G$의 한 maximal torus $T$에 대하여, adjoint representation $\Ad: G\rightarrow \Aut(\mathfrak{g})$를 $T$로 제한하여 $\mathfrak{g}$를 $T$-module로 볼 수 있다. 그럼 이를 통해 $T$의 representation $\Ad\vert_T: T \rightarrow \Aut(\mathfrak{g})$를 얻고, 따라서 $\mathfrak{g}$의 weight decomposition을 얻게 될 것이다.

한편 우리는 adjoint action $\Ad$의 명시적인 정의로부터, $T$가 trivial하게 act하는 $\mathfrak{g}$의 subspace를 정확히 알고 있다. 즉 $T$의 Lie algebra $\mathfrak{t}$를 생각하면, $T$가 abelian이라는 사실로부터 $\mathfrak{t}$ 위에서는 이 action이 identity가 되는 것을 안다. 이 때 identity에 해당하는 linear functional은 zero map이므로, 우리는 다음의 decomposition

\[\mathfrak{g}=\mathfrak{g}_0\oplus\bigoplus_{\alpha\neq 0}\mathfrak{g}_\alpha\tag{2}\]

를 얻는다.

이제 우리는 앞선 논의를 Lie algebra의 언어로 바꾸어 쓸 것이다. 그 전에 우리의 관심을 다소 제한시킬 필요가 있다. 우선 임의의 Lie algebra $\mathfrak{g}$가 semisimple이라는 것은 $\mathfrak{g}$가 simple Lie algebra들의 direct sum이라는 것이며, 여기서 simple Lie algebra는 그 ideal이 $0$과 자기자신 뿐인 non-abelian Lie algebra를 의미한다. 만일 $\mathfrak{g}$가 semisimple Lie algebra라면, 다음의 식

\[( X,Y)=\tr(\ad_X\ad_Y)\]

으로 정의한 $(-,-): \mathfrak{g}\times\mathfrak{g}\rightarrow \mathbb{K}$이 non-degenerate이며 그 역도 성립한다는 것을 보일 수 있다. 그럼 우리는 이 “내적”으로부터 weight들의 기하학에 대해 살펴볼 수 있게 된다.

따라서 $\mathfrak{g}$가 semisimple Lie algebra라 하자. 그럼 $\mathfrak{g}$의 Lie subalgebra $\mathfrak{h}$가 Cartan subalgebra라는 것은 $\mathfrak{h}$가 maximal abelian Lie algebra이며, 각각의 $H\in \mathfrak{h}$에 대하여 $\ad_H$가 diagonalizable인 것이다. 이는 semisimple Lie algebra를 가지는 compact Lie group $G$로 한정한다면, Lie correspondance에 의하여 정확히 $G$의 maximal torus의 Lie algebra에 해당하는 것이다.

이를 바탕으로 위의 decomposition (2)를 살펴보면 $\mathfrak{g}_0$은 정확히 Cartan subalgebra $\mathfrak{h}$에 해당하는 부분이 되며 $\mathfrak{g}_\alpha$들 위에서는 torus $T$가 act하므로 그 미분 $\ad$를 통해 $\mathfrak{h}$가 act한다. 이제 다음을 정의하자.

정의 4 Semisimple Lie algebra $\mathfrak{g}$와 $\mathfrak{g}$의 Cartan subalgebra $\mathfrak{h}$에 대하여,

\[\Phi=\left\{\alpha\in \mathfrak{h}^\ast\setminus\{0\}\mid \mathfrak{g}_\alpha\neq 0\right\}\]

의 원소들을 $\mathfrak{g}$의 root라 부른다. 이 때

\[\mathfrak{g}_\alpha=\left\{X\in \mathfrak{g}\mid [H,X]=\alpha(H)X\text{ for all $H\in \mathfrak{h}$}\right\}\]

이다. (§리 군, ⁋정의 19)

즉, semisimple Lie group $G$와 $G$의 maximal torus $T$, 그리고 $T$의 Lie algebra $\mathfrak{t}$를 생각하면, $T$의 adjoint action의 weight decomposition은 다음의 root space decomposition

\[\mathfrak{g}=\mathfrak{t}\oplus \bigoplus_{\alpha\in \Phi} \mathfrak{g}_\alpha\]

을 준다. 우리가 이들을 weight 대신 별도로 root라 부르는 이유는 위에서 언급한 것과 같이 $\mathfrak{g}$ 위에 잘 정의된 내적을 통해 이들이 root system을 이루기 때문이다.

정의 5 유한차원 벡터공간 $E$와 그 위에 정의된 inner product $( -,-)$을 고정하자. $E$의 non-zero vector들의 유한한 집합 $\Phi$가 root system이라는 것은 다음의 조건들이 만족되는 것이다.

1. $\Phi$의 원소들이 $E$를 span한다.
2. 만일 $\alpha\in \Phi$이고 $c\in \mathbb{R}$이라면 $c\alpha\in \Phi$이기 위해서는 $c=\pm 1$이어야 한다.

3. 각각의 root $\alpha\in\Phi$에 대하여, $\Phi$는 $\alpha$에 수직인 초평면에 대한 대칭이동 $s_\alpha$에 대해 닫혀있다. 즉, 임의의 $\alpha,\beta\in \Phi$에 대하여

   \[s_\alpha(\beta):=\beta-2\frac{(\beta,\alpha)}{(\alpha,\alpha)}\alpha\in \Phi\]

   이다.

4. 임의의 root $\alpha,\beta\in\Phi$에 대하여, 다음 식

   \[\langle \beta,\alpha\rangle:=2\frac{(\beta,\alpha)}{(\alpha,\alpha)}\]

   은 항상 정수이다.

Semisimple Lie algebra $\mathfrak{g}$의 Cartan subalgebra $\mathfrak{h}$를 고정하자. 그럼 Killing form $(-,-): \mathfrak{h}\times \mathfrak{h}\rightarrow \mathbb{K}$으로부터 canonical isomorphism

\[\mathfrak{h}\rightarrow\mathfrak{h}^\ast: v\mapsto (-,v)\]

이 존재하며 이를 통해 $\mathfrak{h}^\ast$를 Euclidean space로 볼 수 있다. 명시적으로, 만일 $\alpha,\beta\in \mathfrak{h}^\ast$이고 이에 대응되는 $\mathfrak{h}$의 원소들이 $v_\alpha,v_\beta$라 한다면

\[(\alpha,\beta)=(v_\alpha,v_\beta)=\beta(v_\alpha)\]

로 주어진다. 그럼 이제 다음이 성립한다.

명제 6 정의 4에서 정의한 root들의 모임 $\Phi$는 $\mathfrak{h}^\ast$의 root system이다.

증명

근계의 성질들

기본적으로 우리가 관심을 갖는 대상은 정의 4에서 정의한, semisimple Lie algebra $\mathfrak{g}$와 그 Cartan subalgebra $\mathfrak{h}$가 정의하는 root system $\Phi$이다. 이를 살펴보기 위해 우리는

Inner product space $V$의 root system $\Phi$를 고정하자. 그럼 우리는 임의의 root $\alpha\in \Phi$에 대한 reflection

\[s_\alpha(v)=v-2\frac{(v,\alpha)}{(\alpha,\alpha)}\alpha=v-\langle v,\alpha\rangle \alpha\]

을 생각할 수 있다. 이는 벡터 $\alpha$가 정의하는 초평면에 대한 대칭이동이다. 이러한 대칭이동들로 생성되는 $\Omat(V)$의 subgroup을 우리는 root system $\Phi$의 Weyl group이라 부르기로 하였다.

본질적으로 이는 기하학적 대상이므로 우리는 이를 살펴보아 기하학적 직관을 얻을 수 있다. 가령 우리는 임의의 root system에 대한 Weyl group이 유한하다는 것을 보일 수 있다.

명제 8 임의의 root system $\Phi$에 대하여 그 Weyl group은 유한하다.

증명

정의 5의 셋째 조건에 의하여 $W(\Phi)$의 원소들은 유한집합 $\Phi$ 위에 act한다. 한편 이 action $W\rightarrow S_\Phi$는 faithful action이다. 만일 어떠한 $w\in W$가 $\id_{\Phi}$로 옮겨진다면, 정의 5의 첫째 조건에 의하여 $w\in W$는 $E$의 원소 전체를 고정하는 reflection이고 따라서 $w$는 $W$의 identity이다.

이제 다음의 예시들을 살펴보자.

예시 9 우선 standard Euclidean space $\mathbb{R}^{n+1}$을 생각하고, $\mathbb{R}^{n+1}$의 subspace

\[V_n=\left\{(x_1,\ldots, x_{n+1}\mid x_1+\cdots+x_{n+1}=0\right\}\]

을 생각하자. 우리는 이 벡터공간의 부분집합

\[\Phi(A_n)=\left\{e_i-e_j\mid 1\leq i\neq j\leq n+1\right\}\]

을 생각한다. 그럼 이 집합이 정의 5의 조건을 모두 만족하는 것을 안다. 첫째 조건인 $\Phi(A_n)$이 $V_n$을 span하는 것과, 둘째 조건이 성립하는 것은 자명하다. 셋째 조건의 경우, 임의의 벡터 $\mathbf{x}=(x_1,\ldots, x_{n+1})$와 임의의 $\mathbf{e}_{ij}=e_i-e_j$에 대하여 다음 식

\[s_{ij}(\mathbf{x})=\mathbf{x}-\langle \mathbf{x}, \mathbf{e}_{ij}\rangle\mathbf{e}_{ij}=(x_1,\ldots, x_{n+1})-(x_i-x_j)\mathbf{e}_{ij}\]

이고 이는 $\mathbf{x}$의 $i$번째와 $j$번째의 성분을 바꾼 것으로 주어진다. 따라서 이로부터 정의 5의 셋째 조건이 성립하는 것을 알고 넷째 조건은 자명하다. 또, 위의 계산으로부터 $W(\Phi(A_n))$은 $\Phi(A_n)$의 각각의 성분을 교환하는 것으로 주어지는 것을 안다. 즉 $W(\Phi(A_n))\cong S_{n+1}$이다.

비슷하게 다음의 예시를 생각할 수 있다.

예시 10 이번에는 standard Euclidean space $\mathbb{R}^n$을 생각하자. 이번에는 다음 집합

\[\Phi(D_n)=\left\{\pm e_i\pm e_j\mid 1\leq i \neq j\leq n\right\}\]

을 생각한다. 이들 벡터들이 $\mathbb{R}^n$을 span하는 것은 자명하다. 이번에는 임의의 $\mathbf{e}_{ij}^\pm =e_i\pm e_j$들이 어떠한 reflection을 정의하는지를 살펴보아야 한다. 우리는 $e_i-e_j$들이 벡터 $\mathbf{x}$의 $i$번째와 $j$번째 성분을 바꿔주는 것을 알고 있으며 따라서 $e_i+e_j$가 어떠한 reflection을 정의하는지를 알뗜 충분하다. 즉 다음의 계산

\[s_{ij}^+(\mathbf{x})=\mathbf{x}-\langle\mathbf{x}, \mathbf{e}_{ij}^+\rangle\mathbf{e}_{ij}^+=(x_1,\ldots, x_n)-(x_i+x_j)\mathbf{e}_{ij}\]

을 생각하면, $s_{ij}^+$는 주어진 벡터의 $i$번째 성분과 $j$번째 성분을 바꾼 후 부호까지 반대로 바꾸어주는 것이다. 즉 Weyl group은 semidirect product

\[(\mathbb{Z}/2\mathbb{Z})^{n-1}\rtimes S_n\]

이 된다.

한편, 우리는 $\mathbb{R}^n$의 부분집합

\[\Phi=\{e_1,\ldots, e_n\}\]

이 root system이 되는지를 생각할 수 있으며, 어렵지 않게 이들이 실제로 $\mathbb{R}^n$의 root system을 이룬다는 것을 확인할 수 있다. 동시에 이 과정에서 우리는

위의 예시들에서 살펴볼 수 있듯이 root system을 묘사하기 위해 모든 root들이 필요한 것은 아니다. 가령 $\Phi(A_n)$의 경우,

\[e_i-e_k=(e_i-e_j)+(e_j-e_k)\]

이 성립하며 이로부터 $\Phi(A_n)$을 묘사하기 위해서는 $e_i-e_{i+1}$ 꼴의 원소들만 필요함을 안다. 이와 비슷한 방식으로 우리는 다음을 정의한다.

정의 11 Root system $\Phi$에 대하여, 우리는 $\Phi$의 부분집합 $\Phi^+$가 positive root들의 부분집합이라는 것은 각각의 root $\alpha\in \Phi$에 대하여, $\alpha$와 $-\alpha$ 중 정확하게 하나만이 $\Phi$에 속하며, 임의의 두 $\alpha,\beta\in \Phi^+$가 주어질 때마다 $\alpha+\beta\in \Phi^+$ 또한 성립하는 것이다. Simple root들의 모임 $\Phi^+$을 고정하였을 때, $\Phi^+$의 원소 $\alpha$가 simple root라는 것은 $\alpha$를 $\Phi^+$의 두 원소들의 합으로 나타낼 수 없는 것이다.

따라서 simple root들 사이의 정수값들

\[\langle\alpha_i,\alpha_j\rangle=2\frac{(\alpha_i,\alpha_j)}{(\alpha_j,\alpha_j)}\]

들이 어떻게 정의되었는지만 안다면, 임의의 root $\alpha_j$에 대한 reflection $s_j$가 다른 root $\alpha_i$을 어떻게 옮기는지를 알 수 있고 따라서 이들이 Weyl group에 대한 정보를 모두 갖고 있다.

이제 root system $\Phi$와 simple root들의 모임 $\Delta=\left\{\alpha_1,\ldots, \alpha_l\right\}$이 고정되었다고 하자. 그럼 Cartan matrix는 다음과 같이 정의된다.

정의 12 위와 같은 세팅에서, 다음의 행렬

\[A=(a_{ij})_{1\leq i,j\leq l},\qquad a_{ij}=\langle \alpha_i,\alpha_j\rangle\]

을 Cartan matrix라 부른다.

Root system의 정의에 의하여 각각의 성분 $a_{ij}$는 정수이다. 또 각각의 $i$에 대하여 $a_{ii}=2$인 것 또한 자명하다.

한편, 우리는 다음의 식

\[\langle\alpha,\beta\rangle \langle\beta,\alpha\rangle=4\frac{(\alpha,\beta)^2}{\lvert\alpha\rvert^2\lvert\beta\rvert^2}=4(\cos\theta)^2\]

과, 좌변이 정수라는 사실로부터 임의의 두 root $\alpha,\beta$에 대해 $\langle\alpha,\beta\rangle$이 취할 수 있는 값은 $0, \pm 1, \pm 2$ 뿐인 것을 안다. 여기서 $\cos\theta$는 두 root $\alpha,\beta$가 이루는 사잇각이며 이것이 취할 수 있는 값은

\[0, \pm \frac{1}{2}, \pm \frac{\sqrt{2}}{2}, \pm \frac{\sqrt{3}}{2}, \pm 1\]

이 된다. 여기서 $\pm 1$의 경우는 정의 5의 둘째 조건에 의해 배제되므로 root들은 각각 $30$도 (혹은 $150$도), $45$도 (혹은 $135$도), $60$도 (혹은 $120$도)의 각도만 이룰 수 있다.

예시를 위해 만일 두 root $\alpha,\beta$가 이루는 각이 $30$도이거나 $150$도라 하자. 그럼

\[\langle\alpha,\beta\rangle\langle\beta,\alpha\rangle=3\]

으로부터 $\langle\alpha,\beta\rangle$은 $\pm 1$이거나 $\pm 3$이어야 한다. 이제 다음 식

\[\langle \alpha,\beta\rangle =2\frac{(\alpha,\beta)}{(\beta,\beta)}=\frac{2\lvert\alpha\rvert\lvert\beta\rvert\cos\theta}{\lvert\beta\rvert^2}=\frac{\pm \sqrt{3}\lvert\alpha\rvert}{\lvert\beta\rvert}\]

의 값이 $\pm 1$ 혹은 $\pm 3$이라는 것으로부터 우리는 $\alpha$와 $\beta$의 길이비가 $\sqrt{3}$이어야 함을 안다. 비슷하게 두 root $\alpha,\beta$가 이루는 각이 $45$도 혹은 $135$도라면, 이들 두 root의 길이비는 $\sqrt{2}$여야 하고 $60$도 혹은 $120$도의 경우에는 길이비가 $1$이어야 함을 안다.

한편

바일 군

지금까지의 핵심적인 내용을 요약하면 다음과 같다.

Compact, connected semisimple Lie group $G$에 대하여, 그 maximal torus $T$를 고정하고 adjoint representation $\Ad:G \rightarrow \Aut(\mathfrak{g})$를 $T$로 제한하여 얻어진 weight decomposition을 생각하자. 그럼 weight들은 $\mathfrak{t}^\ast$의 원소이며, 이 위에 정의된 Killing form $(-,-)$에 대하여, nonzero weight들은 root system을 이룬다.

이제 우리가 남은 글에서 설명할 것은 만일 maximal torus $T$를 다른 maximal torus $T’$로 바꾼다면, 이 root decomposition은 어떻게 바뀔지에 대한 것이다. 큰 흐름은 다음과 같다.

1. 고정된 root system $\Phi$에 대하여, $\Phi$는 정의 5의 세 번째 조건으로부터 $s_\alpha$들에 대해 닫혀있다. 이러한 원소들로 이루어진 reflection group을 Weyl group $W(\Phi)$이라 부른다.
2. 한편, 임의의 Lie group 위에 정의된 maximal torus $T$에 대하여, $G$의 adjoint action 중 $T$를 보존하는 것들의 모임을 $W(G,T)=N_G(T)/T$으로 적는다.

우리의 핵심적인 주장은, 위의 상황에서 만들어지는 root system을 $\Phi(G,T)$라 할 경우, $W(\Phi(G,T))\cong W(G,T)$가 성립한다는 것이다. 물론 만일 다른 maximal torus $T’$를 택한다면, 마찬가지로 $W(\Phi(G, T’))\cong W(G, T’)$를 얻을 것이다. 그럼 우리의 두 번째 주장은 canonical하게 $W(\Phi(G,T))\cong W(\Phi(G, T’))$ 그리고 $W(G,T)\cong W(G, T’)$이며 이 canonical isomorphism 하에서 두 isomorphism $W(\Phi(G,T))\cong W(G,T)$와 $W(\Phi(G, T’))\cong W(G, T’)$는 같은 것이라는 것이다. 이에 대한 증명을 모두 하려면 글이 과하게 길어지므로 이 대응들 각각에 대한 설명만 하기로 한다.

위의 흐름에서 $W(\Phi)$는 그 정의가 자명하므로, 이를 자세히 살펴보는 것은 다음 절로 미루고 $W(G,T)$를 우선 정의하자.

정의 6 Compact connected Lie group $G$와, $G$의 maximal torus $T$, 그리고 그 normalizer

\[N=N(T)=\{g\in G\mid gTg^{-1}=T\}\]

에 대하여, $W(G,T)=N/T$를 $G$의 Weyl group이라 부른다.

정의에 의해 Weyl group은 $T$의 선택에 의존하지만, 다음이 성립한다.

정리 7 (Cartan) 임의의 compact connected Lie group $G$의 두 maximal torus $T,T’$는 항상 conjugate이며, 임의의 $G$의 원소는 어떤 maximal torus에 포함되어 있다.

바꾸어 말하자면, 임의의 $G$의 element는, 고정된 maximal torus $T$에 대하여, 적당한 $t\in T$의 conjugate으로 쓸 수 있다.

이제 $W(G,T)$가 root system $\Phi(G,T)$ 위에 어떻게 작용하는지를 살펴봐야 한다. 이는 다음의 식

\[((nT)\cdot \alpha)(H)=\alpha(\Ad(n^{-1})(H))\qquad\text{for all $H\in \mathfrak{t}$}\]

으로 주어진다. 이는 더 자세하게 쓰면 다음과 같다. 임의의 root $\alpha:\mathfrak{t}\rightarrow \mathbb{C}$를 생각하자. 이 root에 해당하는 weight space는

\[g_{\alpha}=\left\{X\in \mathfrak{g}\mid [H,X]=\alpha(H)X\text{ for all $H\in \mathfrak{h}$}\right\}\]

이다. 이제 임의의 $X_\alpha\in \mathfrak{g}_\alpha$와 $n\in N_G(T)$에 대하여, $n$은 $nTn^{-1}=T$를 만족하므로 이를 미분하면 $n$에 의한 adjoint action은 Cartan subalgebra $\mathfrak{t}$ 또한 보존한다. 이제 식

\[\alpha(H)X=[H,X]\text{for all $H\in \mathfrak{t}$}\]

의 양변에 $n$에 의한 conjugation을 취하면,

\[\alpha(H)(nXn^{-1})=[nHn^{-1}, nXn^{-1}]\text{for all $H\in \mathfrak{t}$}\]

을 얻는다. 한편 $nHn^{-1}\in \mathfrak{t}$이고, 이것이 $\mathfrak{t}$와 $n\mathfrak{t}n^{-1}$ 사이의 bijection을 정의하므로 이는 다음의 식

\[[H, nXn^{-1}]=\alpha(H)\cdot (nXn^{-1})\text{for all $H\in \mathfrak{t}$}\]

으로 쓸 수 있다. 즉, 요약하자면 $\mathfrak{t}$에서 $\mathfrak{t}$로의 conjugation map $c(n): X\mapsto nXn^{-1}$을 생각하면, 식 $w(\alpha)=\alpha\circ c(n^{-1})$으로 정의된 $w(\alpha)$ 또한 root이며 이 때 root space 또한 conjugation action을 통해 옮겨지게 된다.

이제 이 대응이 $W(G,T)\cong W(\Phi(G,T))$를 준다는 것이 앞서 언급한 핵심적인 주장이 된다.

한편 정리 7에 의하여, 우리는 임의의 maximal torus $T, T’$가 주어진다면 $T’=gTg^{-1}$을 만족하는 $g\in G$가 존재하게, 이로부터 만들어지는 Weyl group $W(G, T’)$ 또한

\[W(G, T')=N_G(T')/T'=(gN_G(T)g^{-1})/(gTg^{-1})\cong W(G,T)\]

임을 안다. 이 때 명시적인 isomorphism $W(G,T)\rightarrow W(G, T’)$는 당연히 $nT\mapsto gng^{-1}T’$으로 주어진다. 우리의 두 번째 주장은, 이렇게 얻어지는 다음의 diagram

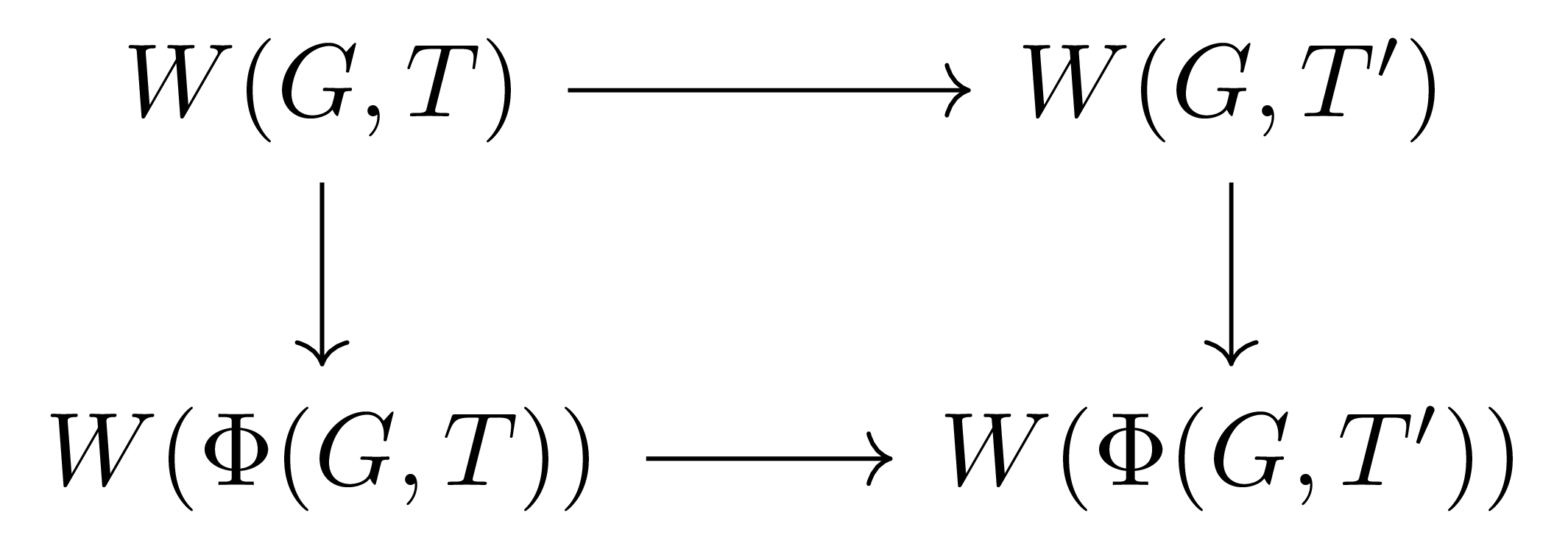
이 commutative diagram이라는 것이다.